Глава VI Пределы

1. Числовые последовательности

Если каждому натуральному числу n поставлено в соответствие действительное число x_n, то множество действительных чисел называется числовой последовательностью или просто последовательностью. Член последовательности с номером n, т.е. число x_n, называется n-ым членом последовательности. Обозначение последовательности: .

2. Монотонность и ограниченность последовательности

Последовательность называется возрастающей (соответственно убывающей), если для любого номера n выполняется неравенство (соответственно ); неубывающей (соответственно невозрастающей), если для любого номера n выполняется неравенство (соответственно ).

Возрастающие, убывающие, невозрастающие и неубывающие последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.

Последовательность называется ограниченной сверху (соответственно снизу), если существует такое число М (соответственно т), что для любого номера n выполняется неравенство (соответственно ). Последовательность называется ограниченной, если она ограничена и сверху, и снизу.

Пример.

Доказать, что последовательность является монотонной.

Решение.

Рассмотрим разность

.

Полученное выражение больше нуля для любого натурального n. Следовательно, . По определению данная последовательность является возрастающей.

Задачи.

Написать первые пять членов последовательности:

6.1. ; 6.2. ;

6.3. ; 6.4. .

Написать формулу n-ого члена последовательности:

6.5.

6.6.

6.7.

6.8.

6.9.

Какие из последовательностей являются монотонными, строго монотонными, ограниченными:

6.10. ; 6.11. ;

6.12. ; 6.13. ;

6.14. ; 6.15. ;

6.16. ; 6.17. .

3. Предел последовательности

Число а называется пределом последовательности , записывается , если для любого, сколь угодно малого , существует номер такой, что при выполняется неравенство .

На -языке это определение можно записать следующим образом:

.

Последовательность, имеющая предел, называется сходящейся. Последовательность, у которой нет предела, называется расходящейся.

Интервал называется -окрестностью точки а. Определение предела имеет следующий геометрический смысл: число а является пределом последовательности , если в любой его -окрестности содержатся почти все члены , или вне этой окрестности находится лишь конечное число членов данной последовательности.

Теоремы о сходящихся последовательностях

1. Сходящаяся последовательность имеет единственный предел.

2. Сходящаяся последовательность ограничена.

3. Предел постоянной равен этой постоянной, т.е. .

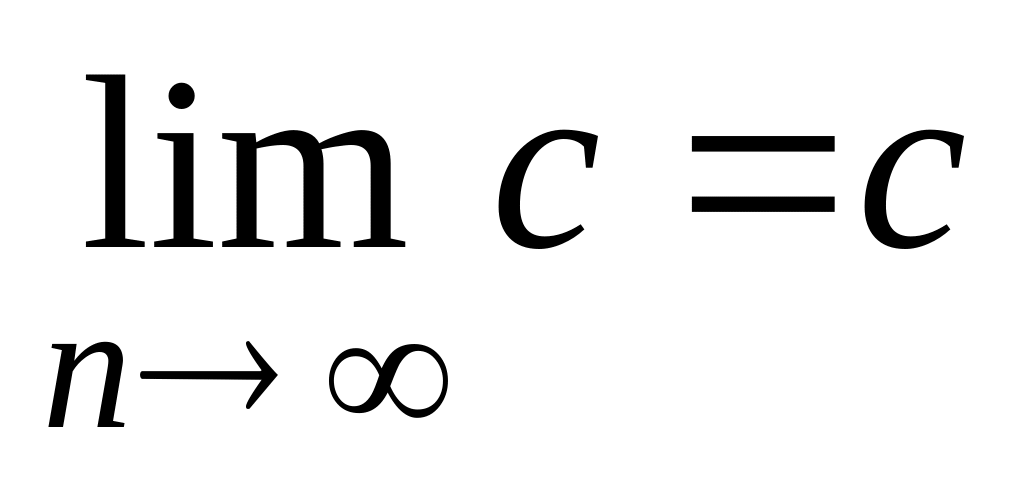4. Пусть существуют пределы последовательностей 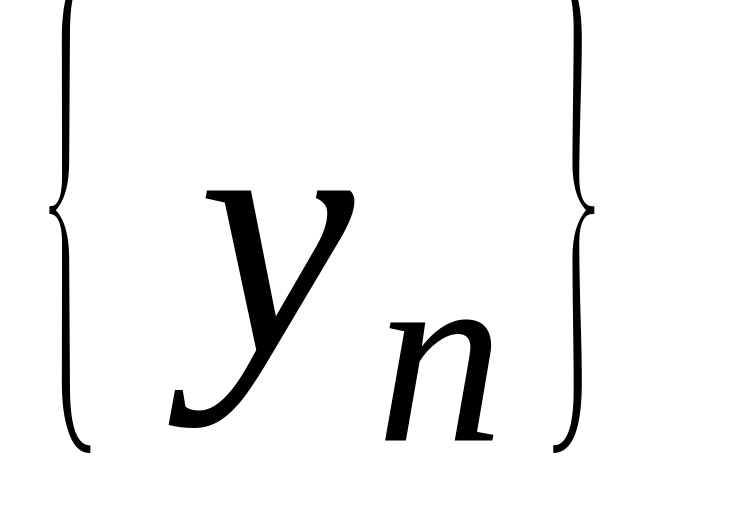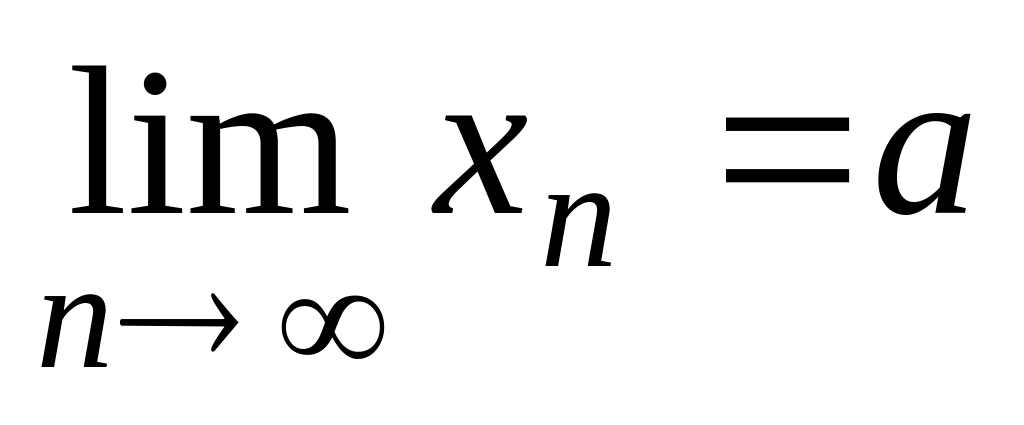и ( и 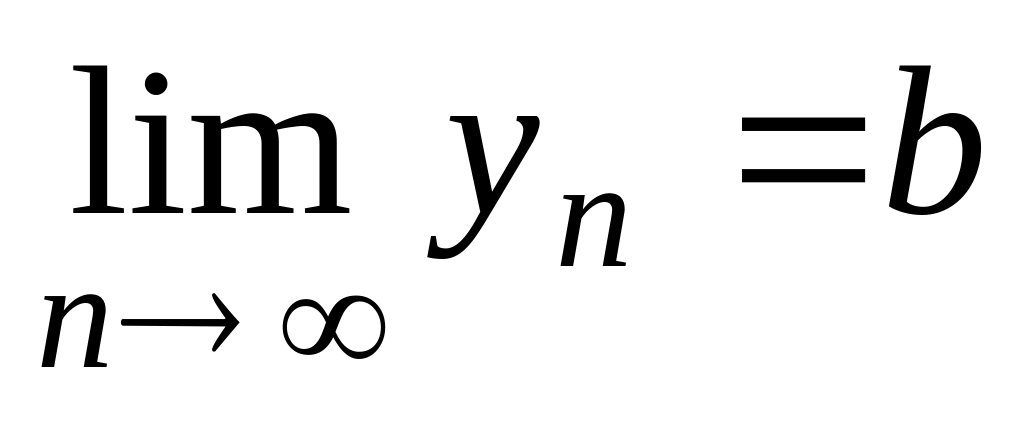). Тогда:

а) существуют пределы последовательностей , причем

;

б) существует предел последовательности , причем

;

в) если b_n  0 при всех , существует предел

последовательности , причем

.

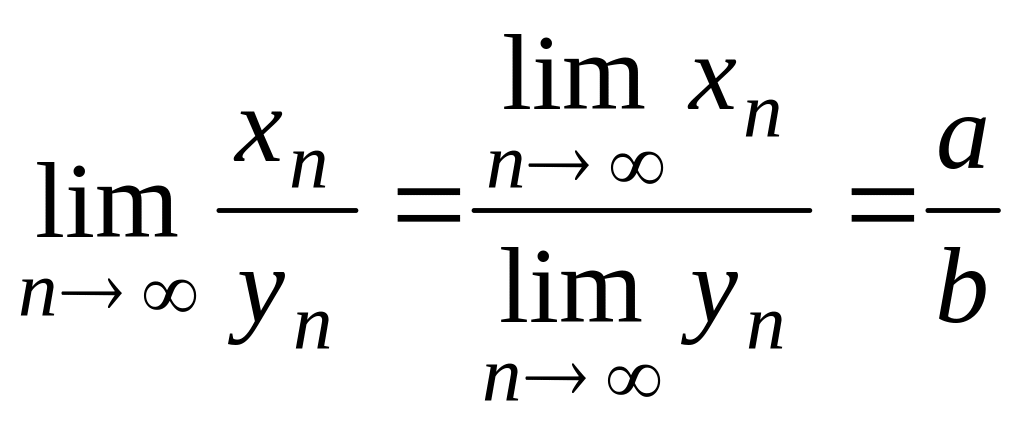4. Бесконечно малые последовательности

Последовательность называется бесконечно малой, если

,

или .

Последовательность называется бесконечно большой, если

,

или .

Свойства бесконечно малых последовательностей

Сумма, разность и произведение двух бесконечно малых последовательностей являются бесконечно малыми последовательностями.

Произведение бесконечно малой последовательности на ограниченную является бесконечно малой последовательностью.

Если – бесконечно малая последовательность и , то – бесконечно большая, и наоборот, если – бесконечно большая последовательность, то – бесконечно малая. Отсюда следует, что

.