2.5.4. Закон равномерного распределения
(законом
равной вероятности) называют распределение
непрерывной случайной величины X
на интервале
,
если в этом интервале случайная величина
сохраняет постоянное значение плотности
распределения, а вне его равна нулю.
Математическое выражение закона в общем виде:
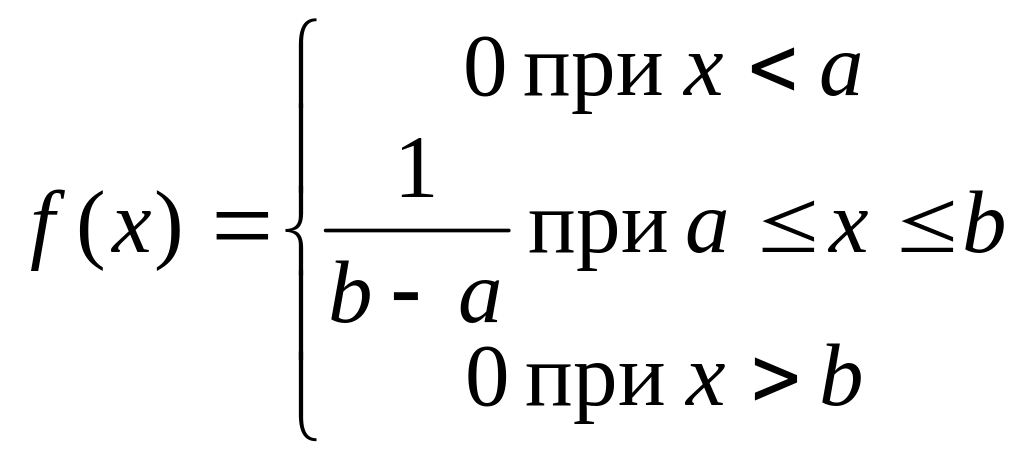
Закономерность имеет простой вид и легко вычисляется, поэтому не имеет смысла приводить её к нормированному виду и табулировать.
Тема 2. Специальный курс теории вероятностей (продолжение)
ЛЕКЦИЯ №4
ПЛАН ЛЕКЦИИ
2.6. Числовые характеристики непрерывных и дискретных распределений.
2.7. Симметричные и ассиметричные распределения.
2.8. Заключение по теме 2.
2.9. Расчёт размерных цепей методом неполной взаимозаменяемости. Применение теоремы Ляпунова.
2.10. Расчёт размерных цепей методом групповой взаимозаменяемости, регулировки и пригонки. Основные сведения.
2.11. Итоги по теме 1.
4.1. Числовые характеристики теоретических
ВЫБОРОЧНЫХ РАСПРЕДЕЛЕНИЙ
Теоретическое распределение характеризует распределение исследуемого признака в генеральной совокупности, а выборочное – в выборке, осуществлённой из этой совокупности. Если выборка репрезентативна, то эти распределения в вероятностном смысле идентичны друг другу и выборочное распределение, как и его числовые характеристики, являются оценками теоретического распределения и его числовых характеристик (параметров).
Числовыми характеристиками теоретического и выборочного распределений на интервале являются (рис.6).
1) математическое
ожидание
и среднее арифметическое
:
где
– объём выборки,
2) дисперсия
и выборочная (эмпирическое) дисперсия
;
3) среднее
квадратическое отклонение
и выборочное (эмпирическое) среднее
квадратическое отклонение
;
4) поле рассеяния
и выборочный (эмпирический) размах:
Рис.
5.1. Закон распределения и его
числовые характеристики
5) медиана
и выборочная (эмпирическая) медиана
:
– среднее значение признака в выборке, слева и справа от которого находятся одинаковое количество наблюдений.
6) мода
и выборочная (эмпирическая) мода
:
– значение признака, которому соответствует наибольшее число наблюдений.
7) коэффициент
относительной асимметрии
:
где
– координата середины поля допуска
– допуск
8) коэффициент
относительного рассеяния
:
9) коэффициент
относительного рассеяния
:
– относительное
среднее квадратичное отклонение
Между коэффициентами и существует зависимость:
Коэффициенты и нашли применение в работах:
1) Цепи размерные PDSO–635–87
2) Балакшин Б.С. Основы технологии машиностроения, 1966г.
Коэффициенты и нашли применение в работах:
1) Методика расчёта размерных цепей на базе теории вероятностей РТМ 32–61 1970.
2) Бородачёв Н.А. Основные вопросы теории точности производства. 1950.
Для стандартного
нормального распределения, определенном
на интервале поля допуска, т.е. когда
,
,
,
.