2.3 Усечённое распределение

Для производства, в общем случае, пригодны не все значения размера X из интервала возможных значений , а лишь те, которые находятся в пределах интервала допустимых значений . Остальные значения отсеивают. Отсеивание негодных значений размера X не ведёт, однако, к нарушениям основных свойств распределений. Новое полученное распределение им веем отвечает, поскольку теперь все значения размера X и з интервала являются достоверным событием и

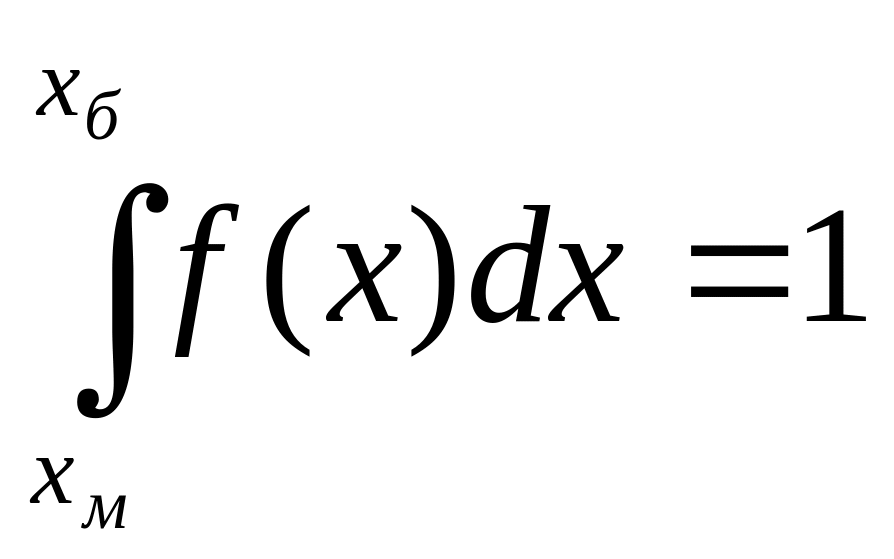
Соответствие негодных значений размера

X и соблюдение указанного условия

тем не менее ведут к

деформации распределения на Рис.3.2. Усечённое распределение

по отношению к исходному

распределению на интервале . Обозначим распределение на интервале через . Можно показать, что для распределений на и на будет иметь место следующая теорема.

Теорема. Распределения и связаны равенством:

Доказательство в кн. Н.А.БОРОДАЧЁВА

"Основные вопросы теории точности производства." М.-Л, изд-во АН СССР, 1950.

Распределение называется усечённым по отношению к распределению . Интервал называется интервалом усечения (рис.3.2.)

Усечённое распределение называется односторонним, если .

Возможны случаи, когда или , а также и

Тема 2. Специальный курс теории вероятностей (продолжение)

ЛЕКЦИЯ 3

ПЛАН ЛЕНЦИИ

2.4. Обрубленное распределение.

2.5. Некоторые виды законов распределения.

2.4. Обрубленное распределение

О собенности инженерных расчетов размерных цепей требуют введения в рассмотрение понятия обрубленного распределения, которое не следует путать с понятием усечённого распределения.

Пусть распределение определено на интервале , тогда в силу 2-го свойства распределений,

Равенство обозначает сходимость Рис.4.1. Обрубленное распределение

несобственного интервала. Отсюда

следует, что для любого сколь угодно малого наперёд заданного числа можно указать такие т , для которых для которых будут выполнятся равенства:

Из равенства можно найти значения и .

Очевидно, значения и есть функции , т.е. и .

Далее можно записать:

При очень малых значениях будет . Поэтому событие является практически достоверным.

Интервал будем называть практическим интервалом изменения случайной величины X или практическим интервалом для распределения , определённую на практическом интервале , обрубленным распределением (рис.4.1.)

Следует отметить, что обрубленное распределение не является распределением в строгом вероятностном смысле, так как 2-е свойство распределений соблюдается приближённо, т.е.

Выбрав тот или иной практический интервал , мы тем самым как бы "обрубаем" и "отбрасываем" концы бесконечной кривой распределения и рассматриваем только обрубленную кривую распределения .

В технологии машиностроения так поступают, например, с нормальным распределением, для которого в качестве концов и практического интервала обычно берут значения, определяемые равенствами:

Практически интервал с такими концами удобно называть стандартным интервалом нормального распределения, чтобы отличить его от других возможных практических интервалов, например или и т.д., а обрубленное нормальное распределение на стандартном интервале – стандартным нормальным распределением.

Пример:

При изготовлении размер X детали подчиняется нормальному распределению

Найти стандартный интервал рассеяния и его длину.

Решение:

Из записи для следует

Отсюда:

В случае нормального распределения ширина практического интервала может быть определена как , где t – коэффициент, определяющий практического интервала.