Затримки в комбінаційних схемах
В комбінаційних схемах, нові значення сигналів на виходах з’являються не одразу ж після встановлення сигналів на входах, а через деякий проміжок часу, який називається затримкою КС. Затримка КС дорівнює сумі затримок максимальної кількості логічних вентилів послідовно ввімкнених між входами та виходами КС. Затримка кожного окремого вентиля (І, АБО, НІ, І-НІ, АБО-НІ) зумовлена тим, що до виходу кожного такого логічного елемента підключена ємність навантаження, що дорівнює сумі вхідних ємностей логічних елементів підключених до даного виходу. Напруга на виході кожного вентиля змінюється не моментально, а по мірі заряду-розряду ємності навантаження. Якщо вихід вентиля переходить з логічного нуля в логічну одиницю, то логічна одиниця встановиться на виході вентилю не одразу, а тоді, коли ємність навантаження зарядиться до напруги, яка відповідає логічній одиниці. Чим більша ємність навантаження та чим менший струм зарядки цієї ємності, тим більша тривалість її зарядки і затримка відповідного логічного елемента. Докладніше про затримки логічних вентилів можна почитати в [1].
Наприклад, нижче наведена схема повного суматора, який сумує значення двох однобітних входів A,B та однобітного входу переносу Cin і виводить результат на однобітні виходи суми S і переносу Cout:
Затримка встановлення сигналу на виході S дорівнює сумі затримок сигналів на двох елементах XOR ввімкнених послідовно:
TS = TXOR + TXOR = 2* TXOR
де TXOR – затримка логічного вентиля XOR;
Затримка встановлення сигналу на виході Cout дорівнює сумі затримок на послідовно ввімкнених елементах XOR, AND, OR:
TCout = TXOR + TAND + TOR
Дешифратори
Дешифратор
– це КС, яка ставить у відповідність
комбінаціям двійкових чисел на
N-розрядному
вході комбінації сигналів на 2N
однорозрядних
виходах. Іноді кількість виходів може
бути меншою ніж 2N,
але зазвичай вона більша ніж N.
Дешифратор
з 2N
виходами називають повним. В таблиці
істинності такого дешифратора кожній
комбінації бітів на вході поставлена
у відповідність ненульова комбінація
бітів на виходах. Якщо дешифратор не
повний, це означає, що існують комбінації
сигналів на входах, для яких всі виходи
будуть неактивні (тобто приймають
значення нуля, якщо вважати, що у виходів
високий активний рівень). Часто дешифратори
мають вхід дозволу роботи (Enable),
який
позначається літерою E
(або С, або CS)
у випадку активного високого рівня
цього сигналу і
(
,
)
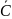у випадку активного низького рівня
цього сигналу.
Якщо
на вході E
присутній
активний рівень (на приклад логічна 1 у
випадку активного високого рівня),
дешифратор працює нормально і виконує
свої функції. Якщо на вході відсутній
активний рівень (на приклад логічний 0
у випадку активного високого рівня),
всі виходи дешифратора будуть неактивні.
Існує багато різновидностей дешифраторів, які будуть розглянуті далі. Для кожного типу дешифраторів ми розглянемо його схему, таблицю істинності та принцип роботи.
Двійковий дешифратор має один N-розрядний вхід, не більше 2N виходів і є одним з найпоширеніших типів дешифраторів. Двійковий дешифратор робить активним лише той вихід, номер якого подано на вхід. Всі інші виходи будуть неактивними.
Наприклад, у двійкового дешифратора з трьохбіовим входом (A2A1A0) буде 23=8 виходів (Q0, Q1, …, Q7). Припустимо, що ці виходи мають високий активний рівень і на вході присутнє число 3 в двійковій системі числення (A2A1A0 = 011b). В такому випадку на виході Q3 буде логічна одиниця, а на всіх інших виходах – логічні нулі. Графічне позначення такого двійкового дешифратора з активним високим рівнем виходів (а) і з активним низьким рівнем виходів (б):
Розглянемо приклад реалізації двійкового дешифратора, графічне позначення якого наведено вище.
Таблиця істинності такого дешифратора:
A2 |
A1 |
A0 |
Q0 |
Q1 |
Q2 |
Q3 |
Q4 |
Q5 |
Q6 |
Q7 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Оскільки дешифратор з нашого прикладу має 8 виходів, для його реалізації необхідно синтезувати 8 логічних функцій. Запишемо їх з таблиці істинності через ДДНФ:
;
;
;
;
;
;
Принципова схема двійкового дешифратора, побудована по логічних рівняннях наведена на рис.1.1, який розташований на наступній сторінці. Для введення сигналу дозволу роботи E, його необхідно завести на всі логічні елементи І, що формують значення на виходах дешифратора. В такому випадку нуль на вході E приведе до нулів на всіх виходах двійкового дешифратора.
Масштабування двійкових дешифраторів.
Існує можливість збільшення розрядності входу двійкового дешифратора і кількості його виходів шляхом з’єднання кількох дешифраторів з меншою розрядністю входу. Для цього дешифратори необхідно сполучити наступним чином:
На
рисунку показано, як на базі дешифраторів
з двухрозрядними входами і чотирма
виходами створити дешифратор, що має
чотирьохрозрядний вхід і 16 виходів (які
пронумеровані цифрами від 0 до 15). Два
старших розряди чотирьохрозрядного
вхідного коду підключено до двухрозрядного
входу дешифратора DC1,
а виходи цього дешифратора, які мають
активний низький рівень, підключені до
входів дозволу роботи
дешифраторів
DC2-DC5
(які теж мають активний низький рівень).
Два молодших розряди вхідного коду
заведені на входи дешифраторів DC2-DC5.
Якщо в двох старших розрядах вхідного
коду будуть нулі, активним буде нульовий
вихід дешифратора DC1.
Оскільки цей вихід має активний низький
рівень, на ньому в такому
Рис.1.1
– Схема повного двійкового дешифратора
з трьохбітним входом
випадку буде присутній нуль, а на інших виходах DC1 будуть одиниці, оскільки ці виходи неактивні. На вході дозволу роботи дешифратора DC2 буде нуль і цей дешифратор буде нормально працювати, а на входах дозволу дешифраторів DC3-DC5 будуть одиниці, тому ці мікросхеми перейдуть в неактивний стан, всі їх виходи будуть неактивні і на них будуть присутні одиниці. В такому випадку, два молодших біта вхідного коду оберуть один з виходів дешифратора DC2, відповідно до числа закодовано в цих двох бітах. Аналогічно, якщо два старших біта міститимуть число 1 (в двійковій формі 01), це призведе до того, що стане активним перший вихід дешифратора DC1, внаслідок чого буде обрано дешифратор DC3, а дешифратори DC2, DC4, DC5 будуть неактивні. В такому випадку два молодших біта вхідного коду зроблять активним вже один з виходів дешифратора DC3. Таким чином, при подачі на чотирьохбітний вхід розробленого комплексного дешифратора двійкових чисел від 0 (0000) до 15 (1111), для кожного такого числа буде активний лише один з виходів, номер якого дорівнює числу, поданому на вхід.
Застосування двійкових дешифраторів.
Розглянемо застосування двійкового дешифратора на прикладі мікросхеми постійної пам’яті, спрощена структурна схема якої наведена нижче:
Як видно з рисунка, інтегральна мікросхема (ІМС) постійної пам’яті складається з дешифратора адреси (DC) і комірок пам’яті (КП). В даному прикладі розглядається пам'ять з розрядністю шини даних 8 біт (виходи D0-D7) і з розрядністю шини адреси 10 біт (входи A0-A9). Отже така ІМС пам’яті буде містити 210 = 1024 восьмирозрядних слів даних. Кожна КП має вхід вибору і вихід даних. Як тільки на вхід вибору надходить одиниця, вихід даних підключається до внутрішньої схеми КП і на ньому встановлюється значення біту, який зберігає КП (0 або 1). Якщо ж на вхід вибору поступає 0, вихід даних КП від’єднується від внутрішньої схеми КП і переходить в третій стан. Кожне слово пам’яті в нашому прикладі складається із 8-ми КП, входи вибору яких підключені до виходу дешифратора, який відповідає цьому слову. Як тільки на вхід дешифратора подається нова адреса, встановлюється в одиницю відповідний вихід дешифратора і підключає КП слова пам’яті з такою адресою до шини даних D0-D7 на виході ІМС. При цьому інші виходи дешифратора приймають значення нуля, тому КП інших слів пам’яті від’єднанні від шини даних D0-D7.
Ще
один спосіб застосування дешифраторів
– нарощування об’єму пам’яті. Нижче
наведено приклад, коли є 4 ІМС постійної
пам’яті, з розрядністю шини адреси 8
біт (об’єм таких ІМС складає 28=256
слів) і необхідно створити на їх основі
блок пам’яті з розрядністю шини адреси
10 біт (об’ємом 1024 слова). Перед пояснення
принципу роботи такого підходу необхідно
зауважити, що багато ІМС мають вхід CS
(Chip Select). Якщо
на такому вході присутній активний
рівень, виходи ІМС з’єднуються з
електричною схемою всередині ІМС. Якщо
ж активний рівень на вході CS
відсутній, виходи ІМС від’єднуються
від внутрішньої логіки і на них
встановлюється так званий третій стан
(не 0 і не 1). Фактично третій стан означає
відсутність сигналу (напруги) на виходах
ІМС. Це не дивно, оскільки в такому
випадку виходи являють собою провідники
не підключені до жодного джерела напруги.
У кожної ІМС пам’яті з даного прикладу
існує два входи
і
,
обоє з активним низьким рівнем. Дані на
виході такої ІМС будуть присутні у
випадку нулів на
і
.
Входи
використовуються для вибору мікросхеми
за допомогою дешифратора, а входи
всіх мікросхем об’єднуються і слугують
входом вибору розроблюваного блоку
пам’яті.
Для об’єднання чотирьох зазначених ІМС в один великий масив пам’яті, необхідно підключити молодші 8 біт 10-бітної адреси до входів адреси мікросхем пам’яті, а два старших біта до входу дешифратора, який має чотири виходи з активним низьким рівнем. Кожен біт 4-х бітної шини даних підключається до відповідного виходу кожної ІМС (виходи D0 всіх мікросхем пам’яті з’єднуються між собою і підключаються до нульового виходу шини даних, виходи D1 з’єднуються між собою і підключаються до першого виходу шини даних і т.д.). В такому випадку до кожної лінії шини даних може бути підключено кілька джерел сигналу, але короткого замикання не відбувається, оскільки в кожен момент часу буде активний вихід лише однієї мікросхеми, який і сформує необхідний логічний рівень на відповідній лінії шини даних. Виходи всіх інших мікросхем будуть знаходитися в третьому стані, тобто будуть від’єднанні від нутрощів ІМС. Отже якщо подати нову адресу на вхід розробленого блоку пам’яті, два старших біта цієї адреси за допомогою дешифратора оберуть одну з мікросхем пам’яті, яка видасть на вихід даних слово, що лежить за молодшими 8 біт адреси. При цьому виходи інших ІМС пам’яті будуть знаходитися в 3-му стані.
Двійкові дешифратори широко використовуються при створенні загальної шини. Пам’ять і периферійні пристрої (таймери, лічильники, UART, USB, порти вводу-виводу, тощо) підключають до сучасних процесорів за допомогою загальної шини. Часто ці компоненти знаходяться в одному адресному просторі і якщо ми записуємо дані за однією адресою, попадаємо в пам'ять, а для іншої адреси запис/зчитування проводиться в/із регістру периферійного пристрою. Нижче у якості прикладу наведено частину адресного простору процесору Cortex A8.
….
З наведеної таблиці видно, що в діапазоні адрес 0x402F0400 – 0x402FFFFF повинна знаходитись внутрішня оперативна статична пам'ять (SRAM) мікроконтроллера, побудованого на базі Cortex A8, а зовнішня пам'ять (External memory) знаходиться в діапазоні адрес 0x00000000 – 0x1FFFFFFF. Регістри UART (universal asynchronous receiver/transmitter) знаходяться в діапазоні адрес 0x44e09000 – 0x44e09FFF. Цей діапазон дозволяє адресувати 4096 (4 Кбайт) 32-х бітних регістрів. Звичайно UART не зобов’язаний використовувати таку велику кількість регістрів, тому на практиці UART містить не більше десятка регістрів, а інші адреси з цього діапазону не використовуються. Порти вводу-виводу GPIO0 знаходяться в діапазоні адрес 0x44E07000 – 0x44E07FFF. Отже в такого процесора може бути максимум 4096 32-розрядних портів вводу-виводу і якщо необхідно щось зчитати/записати з якогось порта, необхідно виконати запис/зчитування слова за адресою цього порта. Отже з використанням подібного підходу всі свої зовнішні пристрої процесор бачить, як комірки пам’яті.
Як це можна реалізувати на практиці? Розглянемо найпростіший випадок, коли адресний простір розбитий на блоки по 8Кбайт. Кожен з цих блоків може бути або оперативною RAM пам’яттю, або постійною ROM пам’яттю, або периферійним пристроєм. Припустимо, що загальна адреса містить 16 біт. В такому випадку молодші 13 біт будуть адресувати комірку всередині 4Кбайтного блоку пам’яті, а старші 16 - 13 = 3 біти будуть адресувати сам блок пам’яті, вибір якого відбувається за допомогою двійкового дешифратора:
Наприклад, якщо ми хочемо зчитати друге слово з постійної ROM пам’яті, необхідно виставити на шину адреси число 0х4002 (0100000000000010 в двійковій системі). Три старші біти, які підключаються до входу дешифратора містять число 2 (010). Отже на виході Y2 дешифратора буде 0, а на всіх інших його виходах буде 1. Нуль на вході ROM пам’яті увімкне цю мікросхему, а одиниця на вході RAM пам’яті вимкне її і переведе виходи RAM в третій стан. Комірки всередині ROM і RAM адресуються 13-тю молодшими бітами на шині адреси.
Можна реалізувати і більш складні конфігурації адресного простору, коли діапазони адрес периферійних пристроїв будуть не однакові. В такому випадку необхідно модифікувати дешифратор адреси таким чином, щоб він виставляв активний рівень на виході, який відповідає певному діапазону адрес, якщо адреса на вході дешифратора потрапляє в цей діапазон.
Двійкові дешифратори також широко використовуються, як складові частини мультиплексорів і демультиплексорів, схеми яких будуть розглянуті в наступних лабораторних роботах.
Дешифратор семисегментного індикатора є ще один широко розповсюдженим типом дешифратора. Семисегментний індикатор – відомий пристрій для відображення чисел у десятинній системі (0-9) та у шістнадцятковій системі (0-9, A-F) числення. Існує два типи семи сегментних індикаторів – з загальним анодом (ЗА) і загальним катодом (ЗК). Ці назви виникли зі способу сполучення світлодіодів в індикаторах.
Для того, щоб засвітити розряд (сегмент) індикатора з ЗА, необхідно підключити загальний анод до плюса джерела живлення і подати логічний нуль на вхід, який відповідає обраному сегменту (A-F). При цьому важливо пам’ятати, що подавати нуль необхідно не одразу ж на вхід індикатора, а через резистор, який задасть струм через світлодіод. Якщо не використати цей резистор, струм через світло діод буде обмежений лише дуже низьким опором відкритого діода, що призведе до виходу світлодіода з ладу внаслідок протікання дуже великого струму і перегріву. Якщо на вхід сегмента індикатора з ЗА подати логічну одиницю, відповідний світло діод не буде зміщений в прямому напрямку, тому він не світитиметься.
Щоб засвітити розряд (сегмент) індикатора з ЗК, необхідно підключити загальний катод до мінуса джерела живлення і через резистор подати логічну одиницю на вхід відповідного сегменту.
Отже якщо нам необхідно вивести на семисегментний індикатор якесь число, необхідно подати на входи такого індикатора певну комбінацію нулів і одиниць, яка призведе до висвічування потрібного числа на індикаторі. Задачу перетворення двійкового числа у відповідний код для входу семисегментного індикатора виконує КС дешифратора семисегментного індикатора. Оскільки сегменти індикаторів з ЗА і ЗК засвічуються різними логічними рівнями, дешифратори індикаторів з ЗА і ЗК матимуть різну таблицю істинності.
Спосіб підключення дешифратора семисегментного індикатора з ЗА:
Таблиця істинності семисегментного індикатора з ЗА (Для індикації десяткових чисел 0-9. Для комбінацій 1010-1111 всі сегменти індикатора горітимуть):
Десяткове число |
D3 |
D2 |
D1 |
D0 |
A |
B |
C |
D |
E |
F |
G |
|||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|||||
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|||||
2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|||||
3 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|||||
4 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|||||
5 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|||||
6 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|||||
7 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|||||
8 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||
9 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|||||
10-15 |
1010-1111 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||
Логічні функції не складно створити самостійно, використовуючи ДДНФ, або ДКНФ.
Дешифратор команд мікропроцесора.
Одним з етапів роботи мікропроцесора є визначення команди, яку необхідно виконати. Цю операцію реалізують за допомогою дешифратора команд. Розглянемо роботу такого пристрою на прикладі дешифратора команд для процесора MIPS [2].
Інструкції процесора MIPS мають розрядність 32 біта і бувають трьох типів:
Register (R-type): Інструкції операцій над двома регістрами з записом результату в регістр. Формат таких інструкцій:
де Op – код операції (operation code). Займає старших 6 бітів. Для всіх команд R-типу Op=0;
funct – код функції, яку виконує команда R-типу (додавання регістрів, зсув регістру, множення, регістрів тощо). Займає 6 молодших біт;
Rs – номер регістру, з якого необхідно взяти перший операнд для виконання інструкції R-типу;
Rt – номер регістру, з якого необхідно взяти другий операнд для виконання інструкції R-типу;
Rd – номер регістру, в який необхідно записати результат виконання інструкції R-типу;
sa – кількість біт для команди операції логічного зсуву.
Immediate (I-type): Інструкції операцій над регістром і числовою константою з записом результату в регістр. Формат таких інструкцій:
де Op – код операції (operation code). Займає старших 6 бітів. Для кожної інструкції I-типу (додавання регістру і константи, тощо) існує свій код команди;
Rs – номер регістру, з якого необхідно взяти перший операнд для виконання інструкції I-типу;
Rt – номер регістру, в який необхідно записати результат виконання інструкції I-типу;
Immediate – другий операнд для виконання інструкції I-типу у вигляді 16-бітної константи;
Jump (J-type): Інструкція безумовного переходу (jump). Формат таких інструкцій:
де Op – код операції jump;
Immediate – 26-бітна константа, з якої шляхом зсуву на 2 розряди вліво можна отримати молодші 28 біт адреси пам’яті програм, куди необхідно здійснити безумовний перехід.
В MIPS процесорі, який буде розроблено в даному курсі лабораторних робіт, будуть підтримуватись наступні інструкції (значення Op і funct взято з [3]):
Назва |
Тип |
Op |
funct |
add |
R |
000000 |
100000 |
addu |
100001 |
||
sub |
100010 |
||
subu |
100011 |
||
and |
100100 |
||
or |
100101 |
||
nor |
100111 |
||
xor |
100110 |
||
slt |
101010 |
||
sll |
000000 |
||
srl |
000010 |
||
sra |
000011 |
||
andi |
I |
001100 |
У даних інструкцій поле funct відсутнє |
ori |
001101 |
||
xori |
001110 |
||
slti |
001010 |
||
addi |
001000 |
||
addiu |
001001 |
||
lw |
100011 |
||
sw |
101011 |
||
beq |
000100 |
||
bne |
000101 |
||
j |
J |
000010 |
|
jal |
000011 |
||
jr |
R |
000000 |
001000 |
Процесор з архітектурою MIPS зчитує інструкції з пам’яті програм і перед тим як їх виконувати визначає тип інструкції за допомогою дешифратора команд (тобто визначає, що саме необхідно робити). Дешифрація команд в MIPS процесорі визначається двома схемами – дешифратором коду операції Op і дешифратором коду функції funct.
Таблиці істинності дешифраторів коду операції і коду функції дозоляють однозначно ідентифікувати операцію і функцію, які необхідно виконати. До входу дешифратору коду операції підключають біти 26-31 інструкції, які містять поле Op. Одиниця на одному з виходів цього дешифратора однозначно ідентифікує операцію. Це саме стосуються і дешифратора коду функції команд R-типу, код операції яких дорівнює нулю. На вхід цього дешифратора підключають біти 0-5 інструкції, які містять поле funct. Одиниця на одному з виходів покаже яку функцію необхідно виконати.
Таблиця істинності дешифратора коду операції Op:
Вхід: 6-бітний код операції Op |
Виходи |
||||||||||||
r_type |
andi |
ori |
xori |
slti |
addi |
addiu |
lw |
sw |
j |
beq |
bne |
jal |
|
000000 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
001100 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
001101 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
001110 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
001010 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
001000 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
001001 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
100011 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
101011 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
000010 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
000100 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
000101 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
000011 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Таблиця істинності дешифратора коду функції funct:
Вхід: 6-бітний код функції funct |
Виходи |
||||||||||||
add |
addu |
sub |
subu |
and |
or |
nor |
xor |
slt |
sll |
srl |
sra |
|
|
100000 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
100001 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
100010 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
100011 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
100100 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
100101 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
100111 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
100110 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
101010 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
000000 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
000010 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
000011 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|