Задание к лабораторной работе № 3 структура «цикл»
В каждом варианте задания необходимо определить требуемые входные и выходные данные, для вычисления предложенных функций составить схемы алгоритмов и программы решения задач. Предусмотреть печать всех входных и выходных данных.
Подготовить контрольные варианты (при необходимости самостоятельно выбрать значение входных данных), отладить программы.
Вариант 1
1. Железнодорожный состав проходит первую треть пути со скоростью V1, а оставшуюся часть пути - со скоростью V2 =50км/ч. Определить скорость на первом участке пути по формуле:
,
если средняя скорость поезда на всем пути Vср = 37,5; 40; 45; 62,5 км/ч.
2. Вычислить значения функции по формуле
где:
постоянная
;
переменные
- целого типа.
На печать выдать значения:
а) входных данных;
б) аргументов
,
изменяющегося в пределах
с шагом
и
,
изменяющегося в пределах
с
шагом
;
в) функции
с точностью до сотых для соответствующих
и
.
При решении контрольного
примера принять:
Вариант 2
2. Вычислить значения функции по формуле
где
постоянная
;
переменные
- целого типа;
- вещественного типа.
На печать выдать значения:
а) входных данных;
б) аргументов
,
изменяющегося в пределах
с шагом
и
,
изменяющегося в пределах
с шагом
;
в) функции с точностью до сотых для соответствующих и .
При
решении контрольного примера принять:
Вариант 3
1. За i-ую секунду от начала движения поезд прошел l метров. Какой путь пройдет поезд за первые t секунд и какой скорости он достигнет по истечении этого времени?
где
Отладку программы произвести для значений l = 4, t =10, 3 ≤ l ≤ 9 c шагом 0,5.
2. Груз массой m перемещают равномерно по прямой в горизонтальной плоскости, прилагая силу, направленную под углом α к горизонту. Определить величину этой силы при изменяющихся значениях угла α и коэффициента трения μ.
,
где 0 α 0,5 рад с шагом 0,1 рад ; 0,1 0,2 с шагом 0,02; m = 10 кг.
2. Вычислить значения функций по формулам:
где:
- переменные целого типа.
На печать выдать значения:
а) входных данных;
б) аргументов
изменяющегося в пределах
с шагом
и
изменяющегося в пределах
с шагом
в) функций
и
с точностью до сотых для соответствующих
и
.
При решении контрольного примера принять:
Вариант 4
1. Найти скорость поезда, при которой маятник длинной l см, подвешенный в вагоне, раскачивается особенно сильно, если длина рельсов L = 12,5 м ; g = 9,81 м/c2
,
где 40 l 80 с шагом 4 см.
2. Вычислить значения функции
при изменении x в пределах /1; 2/ c шагом 0,25 и y в пределах /4,2; 5,1/ c шагом 0,3.
2. Вычислить значения функции по формуле:
,
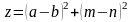где:
переменные:
- целого типа;
- вещественного типа.
На печать выдать значения:
а) входных данных;
б) аргументов
,
изменяющегося в пределах
с шагом
,
и
,
изменяющегося в пределах
с шагом
в) функции с точностью до сотых для соответствующих и .
При
решении контрольного примера принять:
