7. Элементы гармонического анализа

7.1. Ряд Фурье для функции с периодом

Рассмотрим еще один конкретный класс функциональных рядов, которым удобно пользоваться при описании периодических процессов.

Тригонометрическим рядом называется функциональный ряд вида

, (7.1)

где  действительные числа, называемые коэффициентами этого ряда.

Поскольку членами ряда (7.1) являются тригонометрические функции с общим периодом , то в случае сходимости этого ряда на отрезке длиной он сходится на всей числовой оси, а его суммой является некоторая периодическая функция с периодом :

. (7.2)

Очевидно, что каждое слагаемое тригонометрического ряда описывает гармоническое колебание с амплитудой , круговой частотой и начальной фазой . Действительно:

,

где и , откуда амплитуда и начальная фаза гармонического колебания могут быть найдены по формулам:

, .

В связи с этим соотношение (7.2) можно трактовать как разложение функции по гармоникам, то есть провести гармонический анализ этой функции, что в ряде случаев представляет практический интерес.

Коэффициенты разложения функции в тригонометрический ряд могут быть вычислены на основании теоремы: если периодическая с периодом функция является суммой равномерно сходящегося тригонометрического ряда (7.2), то это разложение единственно, причем коэффициенты ряда вычисляются по формулам:

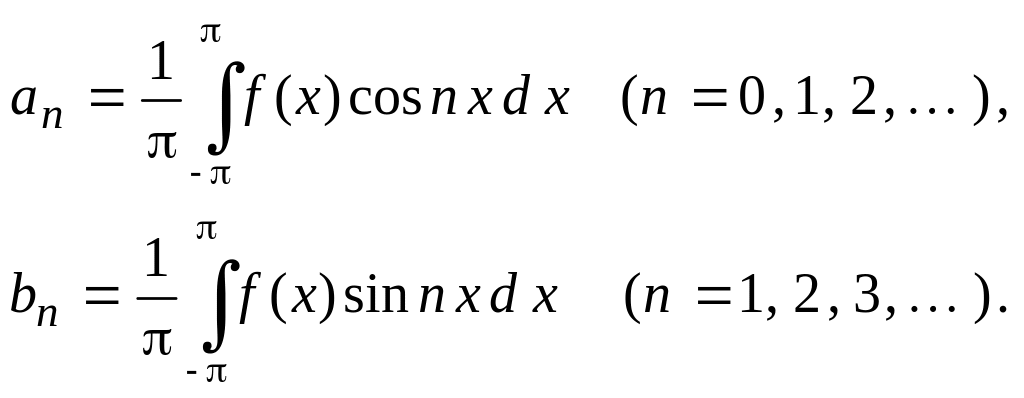(7.3)

Тригонометрический ряд (7.1), коэффициенты которого вычисляются по формулам (7.3), называется рядом Фурье, а коэффициенты этого ряда  коэффициентами Фурье.

Существование интегралов в формулах (7.3) определяет только лишь необходимые условия разложения функции в ряд Фурье, то есть, формально построенный ряд Фурье для функции может расходиться, либо его сумма не будет совпадать с функцией .

Чтобы гарантировать представление функции в виде ряда Фурье, наложим на нее условия, называемые условиями Дирихле:

1) функция должна быть непрерывной на рассматриваемом отрезке , либо должна иметь на нем конечное число точек разрыва рода;

2) эта функция должна быть монотонной на рассматриваемом отрезке, либо иметь на нем конечное число экстремумов.

Достаточные условия разложения функции в ряд Фурье формулируются теоремой (Дирихле): если периодическая с периодом функция на отрезке удовлетворяет условиям Дирихле, то:

1) ряд Фурье (7.1) для этой функции сходится равномерно на всей числовой оси;

2) сумма ряда Фурье равна функции во всех точках непрерывности этой функции;

3) в точках разрыва рода функции сумма ряда Фурье равна среднему арифметическому предельных значений этой функции слева и справа от точек ее разрыва, то есть .

Пример 7.1. Разложить в ряд Фурье функцию

где  целое число.

Р е ш е н и е. Заданная функция (рис. 7.1) является периодической с периодом , удовлетворяет условиям Дирихле и, следовательно, может быть представлена в виде ряда Фурье.

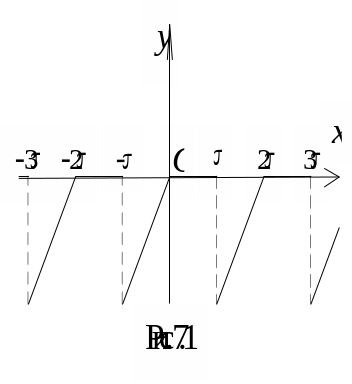
Подсчитаем коэффициенты Фурье по формулам (7.3), применив для вычисления интегралов метод интегрирования по частям:

;

;

.

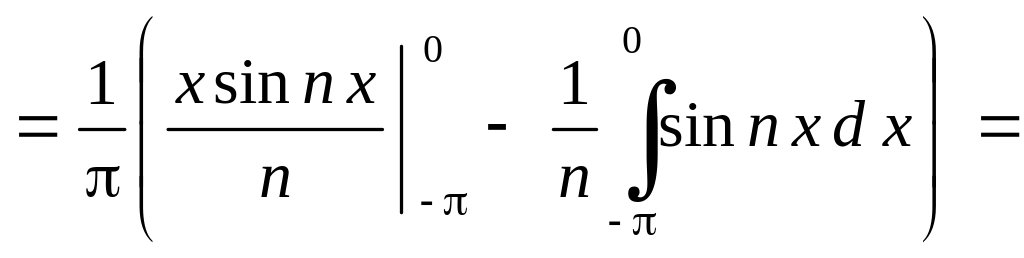
Так как , то и . Тогда разложение заданной функции в ряд Фурье примет вид:

.

Задание 7.1. Разложить в ряд Фурье периодическую с периодом функцию , заданную на отрезке соотношением

Ответ: .