Ответы: 1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
.
2.
Функции
разложить в ряды Маклорена и указать
области сходимости полученных рядов:
1)
;
2)
;
3)
;
4)
.
Ответы:
1)
,
;
2)
,
;
3)
,
;
4)
,
.
3.
Используя таблицу разложений,
функции
представить в виде рядов Тейлора по
степеням разности
и указать области их сходимости:
1)
,
;
2)
,
;
3)
,
;
4)
,
.
Ответы:
1)
,
;
2)
,
;
3)
,
;
4)
,
.
6. Приложения степенных рядов
6.1. Приближенное вычисление значений функций
Числовые и функциональные ряды, в том числе и степенные ряды, находят самое широкое применение в приближенных вычислениях. Сначала рассмотрим вопрос о приближенном вычислении функций с помощью степенных рядов.
Пусть
требуется с заданной точностью
вычислить значение функции
,
которая может быть разложена в
степенной ряд
(6.1)
на интервале
,
в некоторой точке
,
принадлежащей этому же интервалу,
где
радиус сходимости
ряда (6.1).
Ограничиваясь первыми
членами этого ряда, то есть n-ой
частичной суммой ряда
,
получим приближенное искомое значение
функции
в рассматриваемой точке
:
.
(6.2)
Абсолютная
погрешность такого приближения равна
модулю остаточного члена
этого числового ряда:
.
Методы оценки погрешности при приближенном вычислении сумм числовых рядов были рассмотрены раньше (см. подразд. 3.5, 3.6 и 3.7). Однако, если степенной ряд (6.1) является рядом Тейлора, то довольно часто эту погрешность можно оценить с использованием формулы (5.10) остаточного члена ряда Тейлора:
,
(6.3)
где
.
При
вычислении некоторых основных
элементарных функций могут быть
использованы и более простые оценки
погрешности вычислений. Например,
вычисляя значение функции
по приближенной формуле
,
(6.4)
ошибка
вычисления
при
оценивается неравенством
,
(6.5)
а при
можно воспользоваться более простой
оценкой:
.
(6.6)
При
вычислении значений функции
по формуле
(6.7)
погрешность вычислений оценивается как
,
(6.8)
а при вычислений значений косинуса по приближенной формуле
(6.9)
ошибка вычислений составляет:
.
(6.10)
Напомним, что при применении формул (6.7) и (6.9) аргумент синуса и косинуса должен быть задан в радианах.
Для вычисления логарифмов числа целесообразно использовать разложение
,
,
(6.11)
при этом остаток этого ряда может быть оценен с помощью формулы
.
(6.12)
Пример
6.1. Вычислить
с точностью до 0,001.
Р е ш е
н и е. Чтобы воспользоваться разложением
(6.11), положим
,
откуда
.
Затем
определим необходимое количество
членов ряда (6.11), обеспечивающее
заданную точность вычислений
.
При
,
используя оценку (6.12), получим:
,
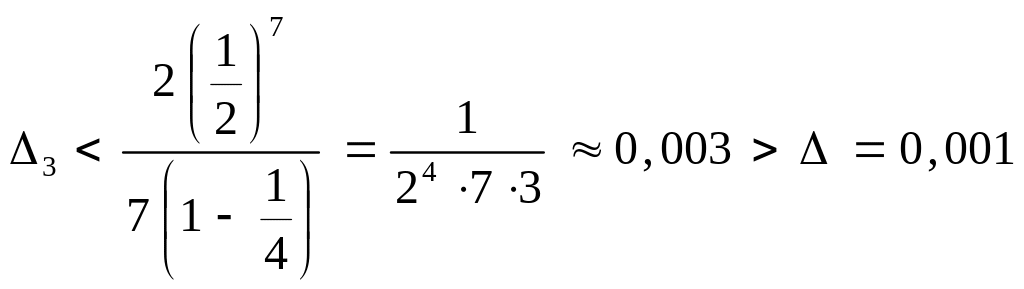а при
будем иметь:
.
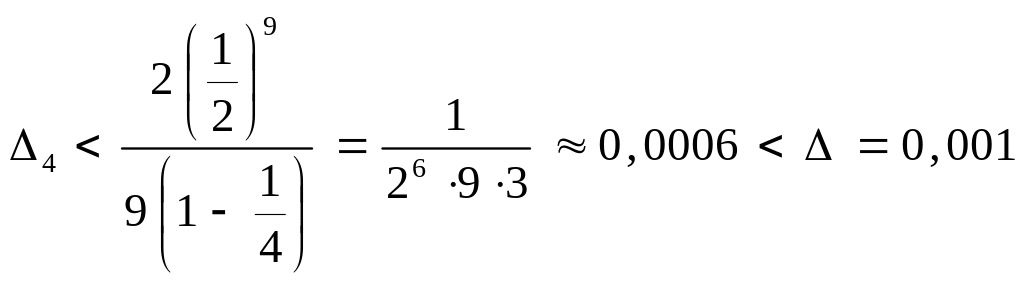Таким образом, суммируя первые четыре члена ряда (6.11), с заданной точностью 0,001 получим:
.
Пример 6.2. С точностью
до 0,00001 вычислить
.
Р е ш е н и е. Сначала преобразуем заданный радикал:
,
а затем,
положив
и
,
воспользуемся биномиальным разложением
(5.23):
.
Для
вычисления корня с заданной точностью
достаточно просуммировать первые
три члена полученного знакочередующегося
ряда, поскольку остаток такого ряда
не превосходит по модулю первого
отброшенного члена ряда:
,
то есть с
заданной точностью
.
Задание 6.1. С точностью до 0,001 вычислить:
а)
;
б)
;
в)
;
г)
.
Ответы: а) 7,389; б) 0,978; в) 1,609; г) 4,309.