5. Степенные ряды

5.1. Степенной ряд и область его сходимости

Среди всех функциональных рядов наибольшее практическое применение нашли так называемые степенные и тригонометрические ряды. Сначала рассмотрим первый из упомянутых классов рядов.

Функциональный ряд вида

, (5.1)

где  некоторые числа, называется степенным рядом, а числа  коэффициентами этого ряда.

В частном случае степенной ряд (5.1) принимает более простой вид:

, (5.2)

который и станет предметом нашего ближайшего изучения, поскольку ряд (5.1) получается из ряда (5.2) подстановкой с последующим переобозначением на .

Заметим, что степенной ряд (5.2) всегда сходится хотя бы в одной в точке , а ряд (5.1) в точке .

Характерная особенность области сходимости степенного ряда устанавливается на основании теоремы (Абеля): если степенной ряд (5.2) сходится в точке , то он абсолютно сходится при всех значениях переменной , удовлетворяющих условию ; если же этот ряд в точке расходится, то он расходится при любом значении , для которого .

На основании этого утверждения нетрудно убедиться в том, что степенной ряд (5.2) сходится в интервале с центром в точке .

Интервалом сходимости степенного ряда (5.2) называется такой интервал , что для всех , принадлежащих данному интервалу, ряд сходится, а для всех , лежащих вне отрезка , ряд расходится, при этом число называется радиусом сходимости этого ряда.

Таким образом, область сходимости степенного ряда (5.2) включает в себя интервал сходимости этого ряда , а также в некоторых случаях точки и , в которых вопрос о сходимости ряда решается в индивидуальном порядке путем исследования сходимости соответствующих числовых рядов, получающихся из степенного ряда (5.2) при и .

Очевидно, что для степенного ряда общего вида (5.1) интервалом сходимости является интервал с радиусом и с центром в точке , то есть интервал .

Для нахождения области сходимости степенного ряда целесообразно воспользоваться формулами вычисления радиуса его сходимости

(5.3)

и

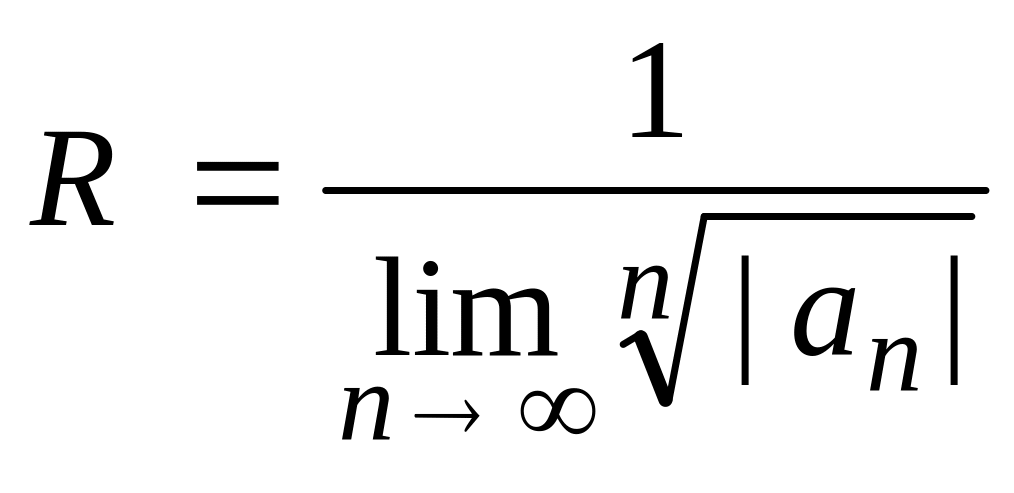, (5.4)

полученных на основе применения признаков Даламбера и Коши абсолютной сходимости этого ряда. Если радиус сходимости степенного ряда по этим формулам вычислить не удается, то следует применить рассмотренные ранее приемы (см. п. 4.2 и 4.3) нахождения области сходимости произвольного функционального ряда.

Пример 5.1. Найти область сходимости степенного ряда

Р е ш е н и е. Исследуемый степенной ряд содержит бесконечное множество нулевых коэффициентов: . Поэтому для вычисления радиуса сходимости заданного ряда нельзя применить формулы (5.3) и (5.4). В связи с этим, рассматривая этот степенной ряд как произвольный функциональный ряд, применим признак Даламбера его абсолютной сходимости:

.

По признаку Даламбера ряд сходится абсолютно при , то есть при , а при ряд расходится. Если , то исходный степенной ряд обращается в расходящийся числовой ряд

Таким образом, область сходимости исследуемого степенного ряда определяется неравенством .

Пример 5.2. Определить область сходимости степенного ряда

Р е ш е н и е. Вычислим радиус сходимости заданного ряда по формуле (5.3). Так как

, ,

то, переходя от дискретной переменной предельного перехода к непрерывной и применив правило Лопиталя раскрытия неопределенности, получим:

.

Затем проверим сходимость ряда на границах интервала сходимости. В точке заданный степенной ряд обращается в знакочередующийся ряд

,

который сходится по признаку Лейбница. Действительно, n-й член этого ряда стремится к нулю:

,

а начиная со второго, абсолютные величины членов этого ряда убывают в силу того, что функция является убывающей функцией при , так как при .

При исходный ряд обращается в знакоположительный ряд

,

который расходится по интегральному признаку Коши:

.

Таким образом, исследуемый степенной ряд сходится на промежутке .

Задание 5.1. Найти области сходимости степенных рядов:

а) ; б) ; в) ;

г) ; д) .

Ответы: а) ; б) ; в) ; г) ; д) .