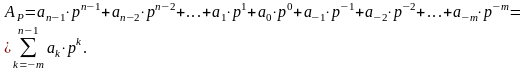Определение. Позиционная система счисления – такая система счисления, в которой “вес” цифры зависит от ее местоположения в записи числа. Например, в числе 1111 одна и та же цифра 1 означает в зависимости от расположения и единицу, и десятку, и сотню, и тысячу.
Любая позиционная система счисления характеризуется своим основанием.
Определение. Основание позиционной системы счисления − количество различных знаков и символов, которые могут быть использованы для изображения цифр в данной системе.
В двоичной системе основание равно двум, то есть в этой системе счисления могут использоваться для записи чисел только две цифры – 0 и 1. В восьмеричной системе основание равно восьми и используются соответственно числа от 0 до 7, в шестнадцатеричной – основание равно 16 и применяются числа от 0 до 15. При записи чисел в шестнадцатеричной системе счисления использовать цифры 10, 11, 12, 13, 14 и 15 неудобно, ведь трудно отличить, например, цифру 12 от двух цифр 1 и 2. По этой причине для обозначений цифр от 10 до 15 в шестнадцатеричной системе счисления используются латинские буквы в алфавитном порядке: 10 – A, 11 – B, 12 – С, 13 – D, 14 – E, 15 – F.
II двоичная арифметика
Арифметические операции с числами в двоичной системе счисления
Пример.
Найти сумму двоичных дробных чисел
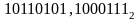и
.
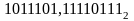Решение.
-
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
+
1
0
1
1
0
1
0
1,
1
0
0
0
1
1
1
02
1
0
1
1
1
0
1,
1
1
1
1
0
1
1
12
1
0
0
0
1
0
0
1
1,
1
0
0
0
0
1
0
12
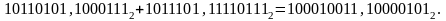
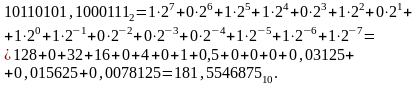
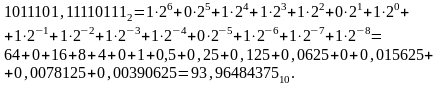
181,554687510+93,9648437510=275,5195312510.
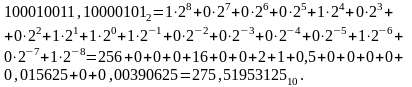
Пример.
Найти разность двоичных дробных чисел
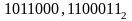и
.
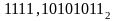Решение.
-
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
[1]
[1]
[1]
[1]
заёмы
из старших разрядов
1
0
1
1
0
0
0,
1
1
0
0
0
1
12
уменьшаемое
1
1
1
1,
1
0
1
0
1
0
1
12
вычитаемое
1
0
0
1
0
0
1,
0
0
0
1
1
0
1
12
разность
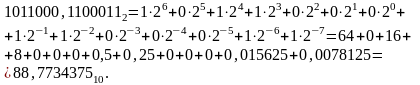
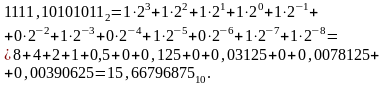
88,773437510-15,667968710=73,1054687510.
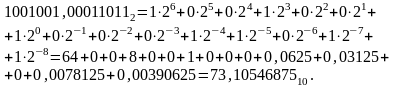
При умножении двух двоичных дробных чисел необходимо придерживаться следующих трёх правил:
числа перемножаются без учета запятых;
в полученном произведении запятая ставится так, чтобы отделить справа столько же знаков, сколько отделено в обоих множителях вместе взятых.
Пример.
Найти
произведение двоичных дробных чисел
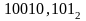и
.
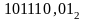Решение. Операция нахождения произведения указанных дробных двоичных чисел требует выполнения сложений неполных произведений, что в свою очередь требует проведения большого количества переносов в старшие разряды. Для повышения наглядности пронумеруем разряды и приведем результаты поразрядных сложений.
-
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
1
1
0
0
1
0,
1
0
12
множимое
2
1
0
1
1
1
0,
0
12
множитель
3
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
переносы в старшие разряды
4
+
1
0
0
1
0
1
0
1
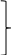
неполные произведения
5
+
1
0
0
1
0
1
0
1
6
+
1
0
0
1
0
1
0
1
7
+
1
0
0
1
0
1
0
1
8
1
0
0
1
0
1
0
1
9
1
1
0
1
0
1
1
1
0
1,
0
1
1
0
12
результат операции произведения
Поразрядное сложение неполных произведений (строки 4 по 8) подробно описано ниже:
-
0 разряд = 1;
1 разряд = 0;
2 разряд = 1;
3 разряд = 0+1=1;
4 разряд = 1+0+1=10 (0 пишем в 4 разряде, 1 переносим в 5 разряд [1]);
5 разряд=[+1]+0+1+0+1=11 (1 пишем в 5 разряде, 1 переносим в 6 разряд [1]);
6 разряд = [+1]+0+0+1+0=10;
7 разряд = [+1]+1+1+0+1+1=101 (1 пишем в 7 разряде, 0 переносим в 8 разряд, 1 переносим в 9 разряд [1]);
8 разряд =0+1+0+0=1;
9 разряд = [1]+0+0+1+1=11;
10 разряд = [1]+1+0+0+0=10;
11 разряд = [1]+1+0+1=11;
12 разряд = [1]+1+0=10;
13 разряд = [1]+0=1;
14 разряд = 1.
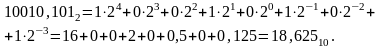
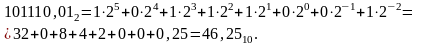
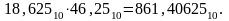
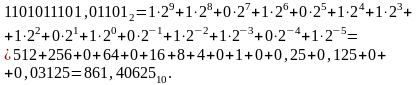
Пример.
Найти
частное двоичных дробных чисел
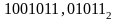и
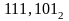с точностью до пяти знаков после запятой.
-
[1]
[1]
1
0
0
1
0
1
1
0
1
0,
1
12
1
1
1
1
0
12
1
1
1
1
0
1
1
0
0
1,
1
1
1
0
02
[1]
1
1
1
0
0
1
0
1
1
1
1
0
1
[1]
1
1
0
1
0
1
1
1
1
1
1
0
1
1
0
0
1
1
0
1
1
1
1
1
0
1
[1]
[1]
[1]
[1]
[1]
1
0
0
0
0
0
0
1
1
1
1
0
1
1
1
0
0
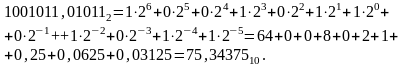
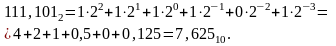
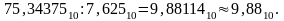
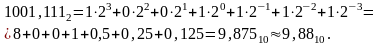
Общая
формула представления числа
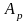в развернутой форме записи в позиционной
системе счисления с основанием
,
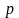имеет вид:
|
(1) |
где
основание системы счисления числа
,
состоящего из
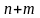разрядов (
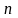разрядов целой части и
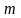разрядов
дробной части);
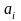цифра
целой части числа
,
отстоящая на
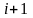позиций от запятой влево,
;
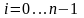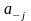цифра дробной части
числа
,
отстоящая на
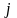позиций от запятой вправо,
;
−
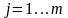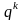вес цифры числа
.
Как видно из (1), развернутая форма записи числа равна сумме произведений каждой цифры числа на соответствующий ее вес цифры.
Из одной системы счисления в другую могут быть переведены, как целые, так и дробные числа. На первый взгляд, такой перевод кажется ординарным, однако для компьютерной техники это далеко непростая задача, так как связана с архитектурой компьютера. Трудность составляет размещение периодических и непериодических дробей, так как ресурсы компьютера не бесконечны. Решением проблемы является округление дробей и задание класса точности чисел, участвующих в вычислениях и появляющихся в их результате.