Лекция 5 Тема: Несимметричные переходные процессы

Цель лекции: Изучить теоретическую часть темы

Несимметричные переходные процессы в электрических системах. Несимметричные режимы возникают вследствие несимметрич­ных коротких замыканий или обрыва одной-двух фаз линии. В первом случае в электрической сети появляется поперечная не­симметрия, во втором - продольная. Строгий математический ана­лиз переходных процессов при несимметрии затруднен тем, что в электрических машинах возникает пульсирующее магнитное поле ротора, которое образует полный спектр высших гармонических составляющих тока. Замена координатных осей А, В, С на систему d, q, 0 не освобождает дифференциальные уравнения от периодических коэффициентов. Поэтому в большинстве практических расчетов учитывается лишь основная гармоника токов или Напряжений. Только при таком ограничении возможно использование метода симметричных составляющих, который наиболее часто применяется для анализа несимметричных КЗ.

Метод симметричных составляющих

Метод симметричных составляющих базируется на математической теории многофазных электрических систем при неодинаковых условиях работы фаз. Сформулируем основные положения метода симметричных со­ставляющих.

1. Любую несимметричную систему токов можно разложить на три симметричные, называемые системами прямой, обратной нулевой последовательностей. Эти системы получили название «симметричные составляющие». Предполагается, что они одновременно циркулируют в рассматриваемой сети в несимметричном режиме.

2. Симметричная система токов прямой последовательности (рисунок 5.1, а) представляет собой три одинаковых по величине вектора, расположенных под углом 120°, вращающихся против часовой стрелки так, что соблюдается нормальное чередование фаз: А - В - С. Соотношения между фазными значениями устанавливаются с помощью оператора

Этот вектор единичной длины имеет аргумент, равный 120°. Если некоторый вектор, например I_А1, умножить на а, то это озна­чает повернуть I_А1 на 120° против часовой стрелки. С помощью вектора а можно выразить токи фаз В и С через ток фазы А: І_B1 = а²І_A1 І_C1 = аІ_A1

3. Симметричная система токов обратной последовательности (рисунок 5.1, б) представляет собой три одинаковых по величине век­тора, расположенных под углом 120° и вращающихся против ча­совой стрелки так, что соблюдается обратное чередование фаз: А - С - В. При этом токи фаз В и С связаны с током фазы А сле­дующим образом: І_B2 = аІ_A2 І_C2 = а²І_A2

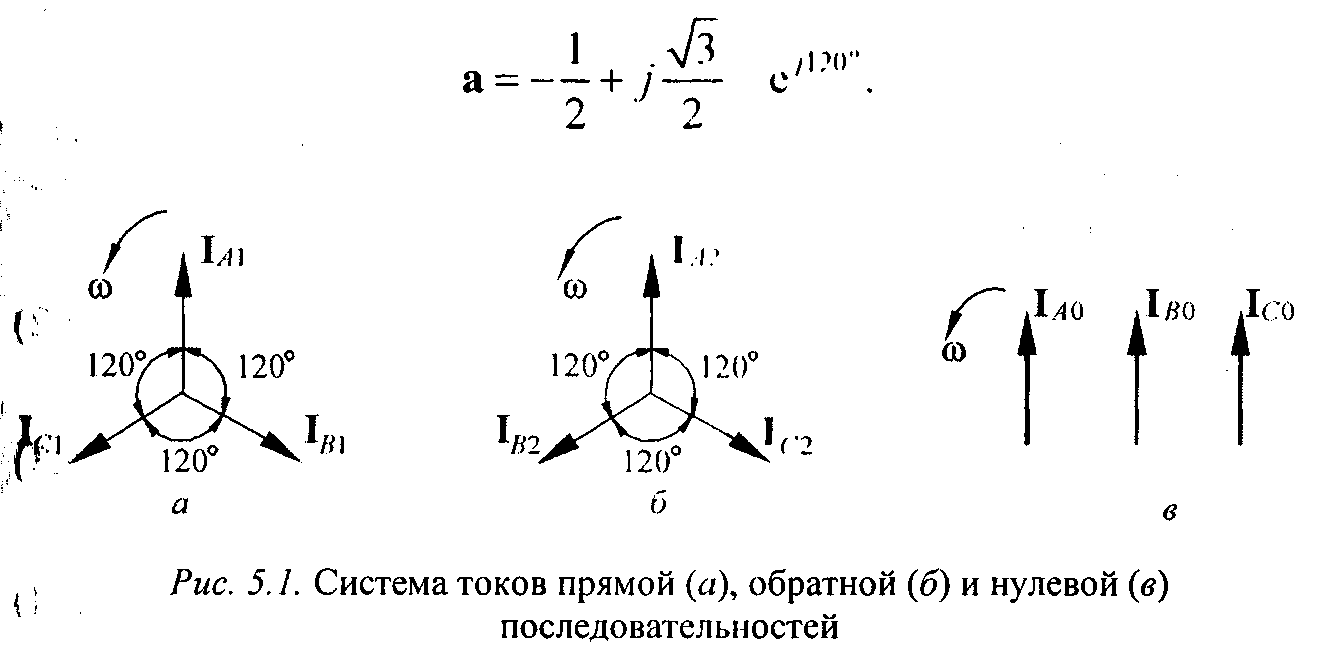
Рисунок 5.1. Система токов прямой (а), обратной (б) и нулевой (в) последовательностей

4. Симметричная система токов нулевой последовательности (рисунок 5.1, в) существенно отличается от прямой и обратной. Она представляет собой систему трех переменных токов, совпадающих по фазе и имеющих одинаковую амплитуду. Эти токи являются, по существу, разветвлением однофазного тока, для которого три про­вода трехфазной цепи составляют один прямой провод, а обратным служит земля или четвертый (нулевой) провод. Появление токов нулевой последовательности в сети означает возникновение в ней несимметричного замыкания на землю. Рассматриваемая несим­метричная система токов допускает только одно разложение на симметричные составляющие. Действительно, представив ток ка­ждой фазы через его симметричные составляющие, получим

I_A ⁼ І_A1 + I_A2 + I_A0,

I_B ⁼ a²І_A1 + aI_A2 + I_A0,

I_C ⁼ aІ_A1 + a²I_A2 + I_A0,

Если I_A ,I_B , I_C заданы, то искомыми являются три величины I_A1 ,I_B2 , I_C0. Они определяются тремя линейными уравнениями, ко­торые допускают только одно решение:

Все соотношения для симметричных составляющих токов справедливы и для напряжений. Рассмотрим разложение на составляющие несимметричной системы токов (рис 4.3, а). С помощью геометрических построе­ний, соответствующих выражениям и найдем ток нуле­вой, прямой и обратной последовательностей (рисунок 5.2, б-г). Если сложить симметричные составляющие в соответствии с выраже­ниями, то получим исходную систему.

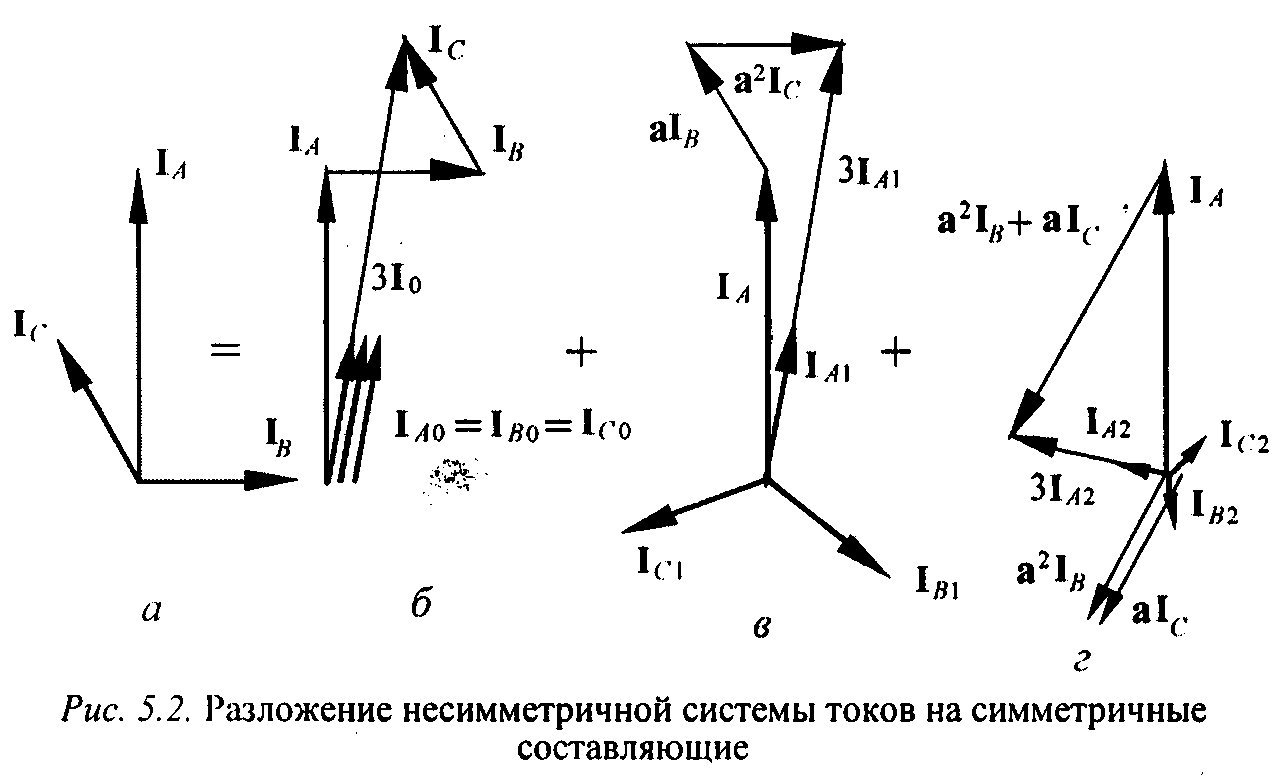
Рис 5.2. Разложение несимметричной системы токов на симметричные сотавляющие

5. В трехфазной цепи в месте КЗ наряду с напряжениями пря­мой последовательности возникают напряжения обратной и ну­левой последовательностей. В ветвях схемы вместе с токами прямой последовательности начинают циркулировать токи об­ратной и нулевой последовательностей.

Для иллюстрации этого положения рассмотрим схему электри­ческой системы, показанную на рисунок 5.4. За положительное на­правление токов примем направление слева направо и допустим, что картина распределения имеет вид, показанный на рисунке. То­гда

для участка 1

для участка 2

для участка 3

Из этих соотношении видно, что ток нулевой последовательности, определяемый по выражению, циркулирует только на участке 2.

Для участков 1 и 2 можно записать следующие соотношения: или

где I₃ - ток в земле. Отсюда,

В симметричных электрических системах токи и напряже­ния схем отдельных последовательностей могут рассматривать­ся независимо друг от друга и быть связаны между собой законами Ома и Кирхгофа.

Если какой-либо элемент цепи симметричен и при протекании по нему токов I₁, I₂, I₀, обладает некоторыми сопротивлениями Z₁, Z₂, Z₀, симметричные составляющие падении напряжения в этом элементе будут равны ∆Z₁ = I₁ Z₁, ∆Z₂ = I₂ Z₂, ∆Z₀ = I₀ Z₀,

Комплексная форма уравнений справедлива ни только для Стационарного режима, но и для переходного, так как токи и на­пряжения при переходном процессе можно представить проекция­ми вращающихся векторов на соответствующую ось. При этом Дифференциальным уравнениям, связывающим комплексные зна­чения, отвечают операторные уравнения, которые при нулевых начальных условиях по своей структуре аналогичны уравнениям стационарного режима, записанным в комплексной форме. Уравнения второго закона Кирхгофа для любого КЗ каждой по­следовательности могут быть записаны в виде U_K1 = E_Σ - Z_1Σ I_K1 , U_K2 = 0 – Z_2Σ I_K2 , U_K0 = 0 – Z_0Σ I_K0: где U_K1 , U_K2 , U_K0 , I_K1 , I_K2 , I_K0- симметричные составляющие Напряжения и тока в месте КЗ; E_Σ - результирующая ЭДС относительно точки КЗ; Z_1Σ , Z_2Σ , Z_0Σ - результирующие сопротивления схем соответствующих последовательностей относительно точки КЗ.

Запись уравнений второго закона Кирхгофа вызывает необхо­димость сформулировать следующее положение метода симмет­ричных составляющих.

Элементы трехфазной сети для токов прямой, обратной и нулевой последовательностей имеют неодинаковые сопротивления. ЭДС генераторов симметричны, т.е. не содержат обратной и нулевой составляющих. Отсюда следует, что: а) в электрических системах существуют только ЭДС прямой последовательности; б) токи обратной и нулевой последовательностей определяются только напряжениями в точке КЗ.

Между системами трех симметричных составляющих все­гда существует связь, задаваемая условиями короткого замыка­ния. Эта связь легко устанавливается путем перевода граничных условий короткого замыкания, заданных через действительные то­ки и напряжения, в условия, заданные через симметричные состав­ляющие.

Параметры элементов электрической системы обратной и нулевой последовательностей

Каждый элемент электрической системы характеризуется па­раметрами прямой, обратной и нулевой последовательностей. Все сопротивления элементов системы, которыми они представлялись в расчетах симметричного КЗ, являются сопротивлениями прямой последовательности. Для элементов, у которых отсутствует маг­нитная связь между фазами (например, реактора), сопротивления различных последовательностей равны между собой и не зависят от чередования фаз. Для элемента, магнитосвязанные цепи которого неподвижны относительно друг друга (например, трансформатора, линии), со­противления прямой и обратной последовательностей равны, так как взаимоиндукция между фазами такого элемента не изменяется при изменении порядка чередования фаз.

С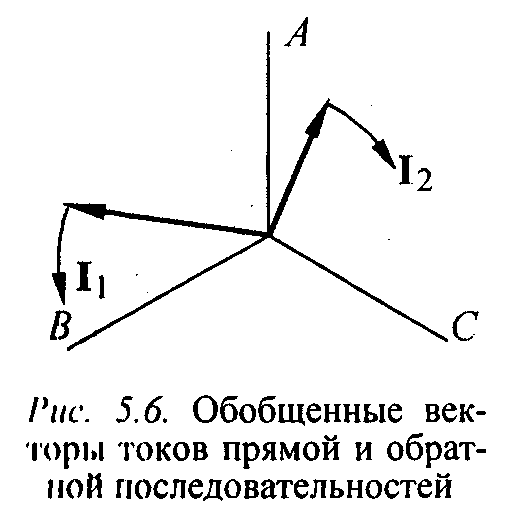 истема токов обратной последовательности отличается от системы прямой последовательности обратным порядком чередо­вания фаз. Обобщенный вектор тока обратной последовательности (рисунок 5.3) вращается в обратную сторону по отношению к вектору прямой последовательности со скоростью.

Рис 5.3. Обобщенные векторы токов прямой и обратной последовательностей

Токи обратной последовательности, протекая по обмоткам ста­тора, создают магнитное поле, вращающееся в сторону, противо­положную направлению вращения магнитного поля реакции статора. Магнитное поле, создаваемое токами обратной последователь­ности, перемещается относительно ротора с двойной синхронной частотой, вызывая пульсирующее магнитное поле двойной часто­ты. Более подробно физическая картина процессов, протекающих в синхронной машине, описана в работе.

Индуктивное сопротивление обратной последовательности может быть определено как отношение приложенного напряжения обратной последовательности к основной гармонике тока обратной последовательности (х₂ = U₂ / І₂ ). Сопротивление неявнополюсной син­хронной машины обратной последовательности в практических расчетах принимается равным ее сверхпереходному сопротивле­нию (х₂ - x"_d). Для явнополюсной машины без демпферной обмотки сопро­тивление обратной последовательности определяется формулой С учетом демпферных обмоток это выражение выглядит так: Токи нулевой последовательности создают только магнитные истоки рассеяния статорной обмотки, меньшие, чем при токах Прямой и обратной последовательностей. Величина индуктивного сопротивления нулевой последовательности х₀ колеблется в широ­ких пред ел ах (от 0.15 x"_d до 0.6 x"_d ).

Формулы для определения сопротивлений прямой, обратной и нулевой последовательности элементов системы электроснабжения приведены в таблица 5.1.

Таблица 5.1.

Наименован. элемента	Трехфазное КЗ		Прямая последов.	Обратная последоват.	Нулевая последоват.
	ИЕ	ОЕ
Синхронный генератор				без ДО с ДО
Воздушная ЛЭП					одноцепная с тросами Х0 = 3,0 Х1, одноцепная без тросов Х0 = 3,5 Х1, двухцепная с тросами Х0=4,7Х1 двухцепная без тросов Х0 = 5,5 Х1
Кабельная ЛЭП					Х0 =(3,5...4,7) Х1, R0 = 10 r L
Токоогранич. реактор					Х0 = Х1
Асинхронный двигатель					Х0 =( 0,15...0,7) Х1
Двухобмот. трансформ.					Определяется соединением обмоток
Синхронный двигатель, компенс.				допускается	Х0 =(0,15...0,7)Х1.