
“ЗАТВЕРДЖЕНО”
на засіданні кафедри оптики протокол № 4 від “ 15 ” грудня 2010г.
Зав. кафедри проф.Сливка О.Г.
Методична розробка
для контролю знань
з курсу "Медична та біологічна фізика"
для студентів 2-го курсу стоматологічного факультету
До модулю №1.
Математична обробка медико-біологічних даних
Приклад одного із варіантів контрольної роботи по темі :“Методи фізичних вимірювань та обробка експериментальних результатів”
Варіант №1
1. Теоретичні запитання
1.1.Що таке вимірювання?. Прямі та непрямі вимірювання ?.
1.2. Що таке функція густини розподілу імовірності та її властивості.
1.3. Середнє квадратичне відхилення окремого вимірювання, середнє квадратичне відхилення середнього значення.
2.
Проведені вимірювання температури
тіла пацієнта за допомогою терморезистора.
Клас точності приладу
![]() .
Максимальне значення діапазону приладу
на якому проводилось вимірювання 500С.
Температура пацієнта виявилась рівною
370С.
Визначити абсолютну та відносну похибку
вимірювання температури.
.
Максимальне значення діапазону приладу
на якому проводилось вимірювання 500С.
Температура пацієнта виявилась рівною
370С.
Визначити абсолютну та відносну похибку
вимірювання температури.
3. Проведені вимірювання температури тіла різних хворих пацієнтів за допомогою терморезистора.
R,Ом |
38,02 |
37.81 |
37.57 |
37.63 |
37,41 |
Визначити середню
температуру пацієнта та довірчий
інтервал в який попадають виміряні
величини з надійністю
![]() =0,95.
Розрахувати результуючу похибку
вимірювання температури із врахуванням
точності приладу (за результатами
завдання №2).
Коефіцієнт Стьюдента для
=0,95
та п’яти вимірювань
=0,95.
Розрахувати результуючу похибку
вимірювання температури із врахуванням
точності приладу (за результатами
завдання №2).
Коефіцієнт Стьюдента для
=0,95
та п’яти вимірювань
![]() =2,45.
=2,45.
4. Записати формулу
для обчислення абсолютної та відносної
похибки непрямих вимірювань величини,
що
визначається за формулою
![]() :
:
Переліки питань та банк тестових завдань для проведення підсумкового модульного контролю №1.
Визначити похідну
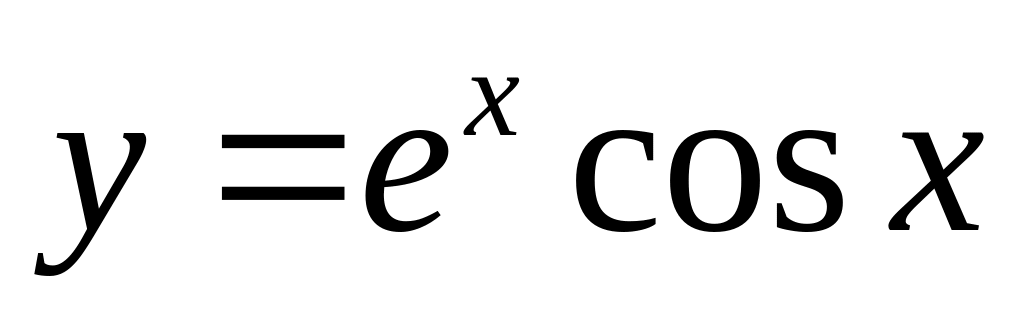
Визначити похідну
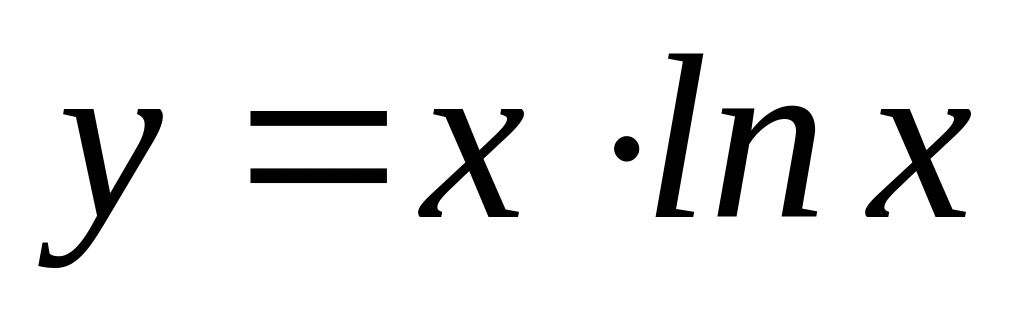
Визначити похідну
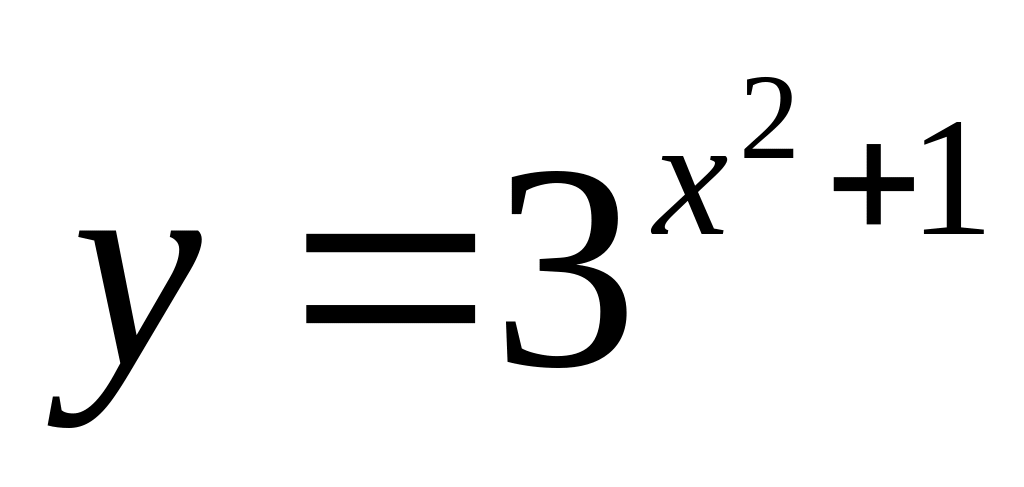
Визначити похідну
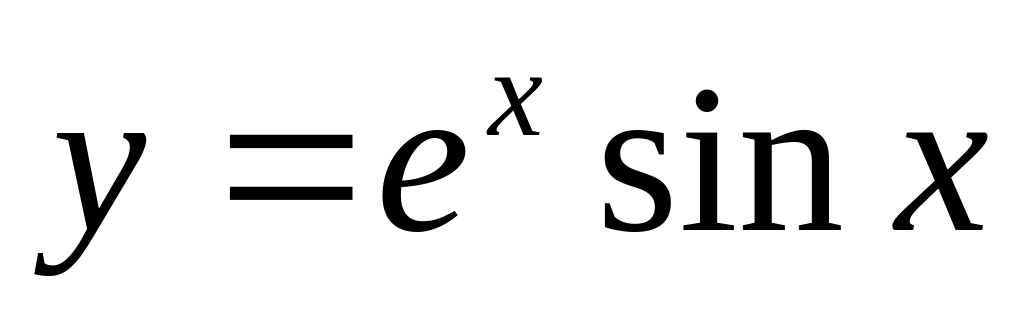
Визначити похідну

Визначити похідну y=x3ex
Визначити похідну y=esinx
Визначити похідну
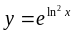
Визначити похідну
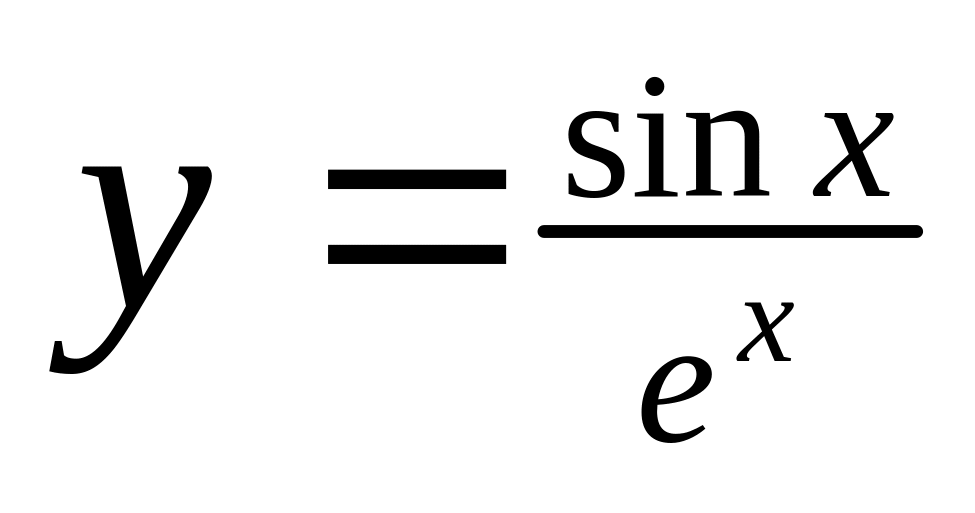
Визначити похідну

Визначити похідну
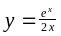
Визначити похідну
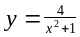
Визначити похідну
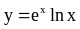
Визначити похідну

Визначити похідну
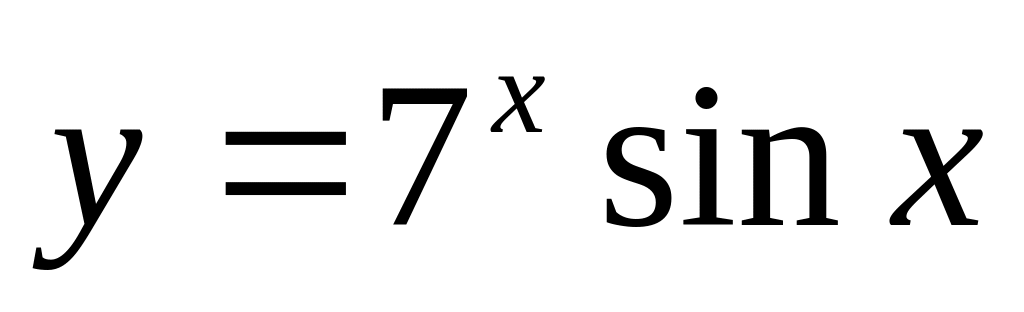
Визначити часткову похідну
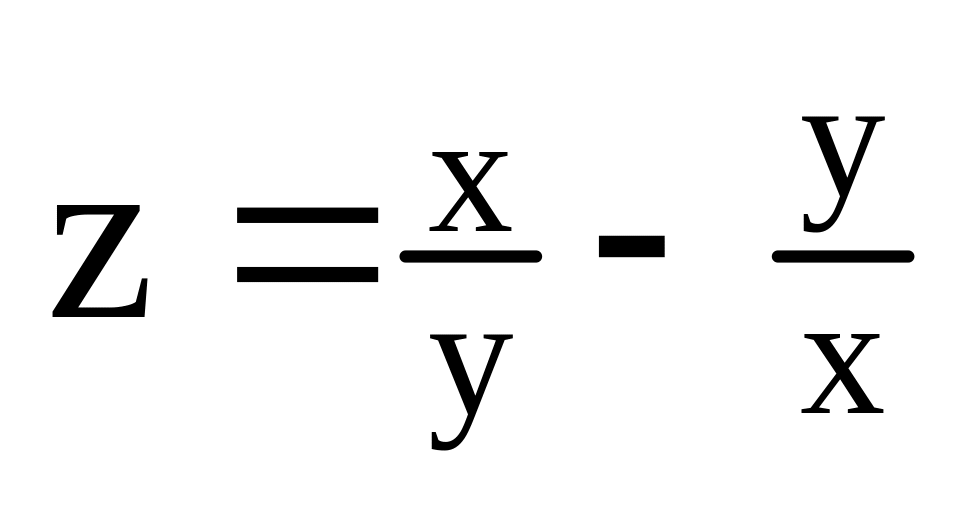
Визначити часткову похідну
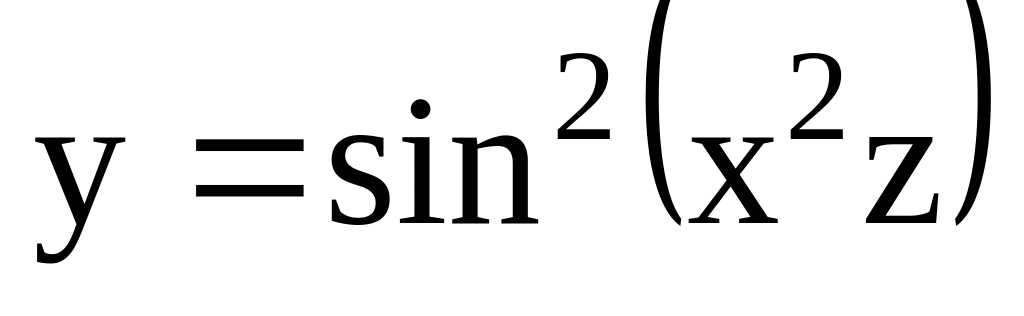
Визначити часткову похідну
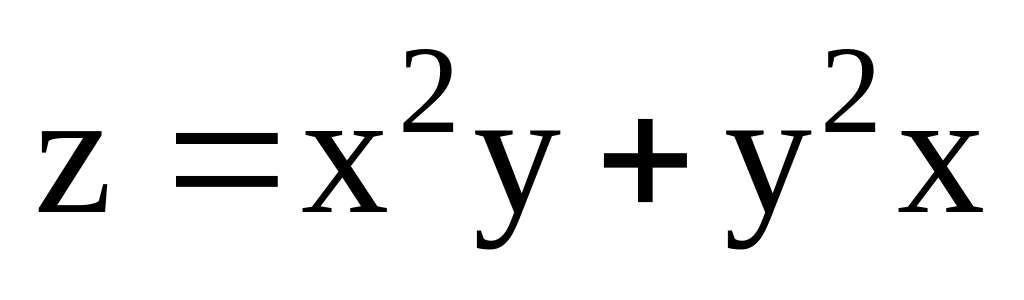
Визначити часткову похідну

Визначити часткову похідну
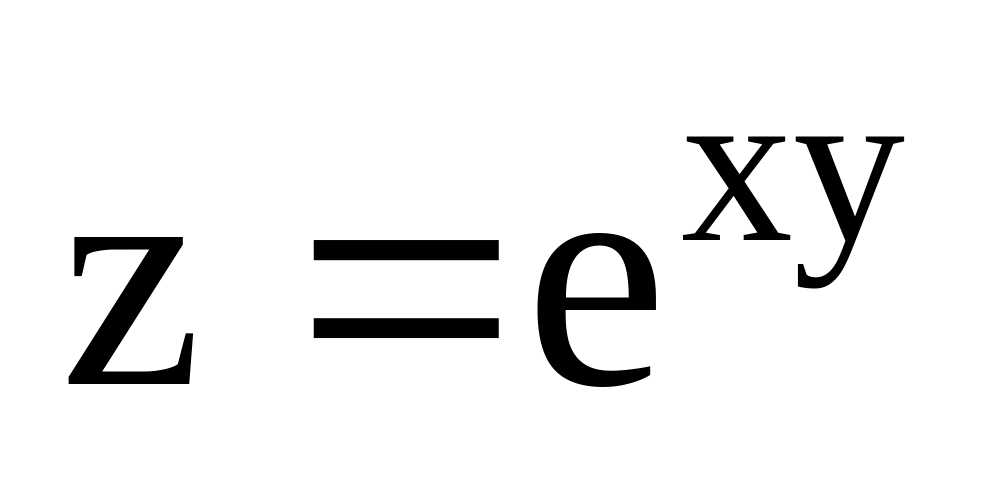
Визначити часткову похідну
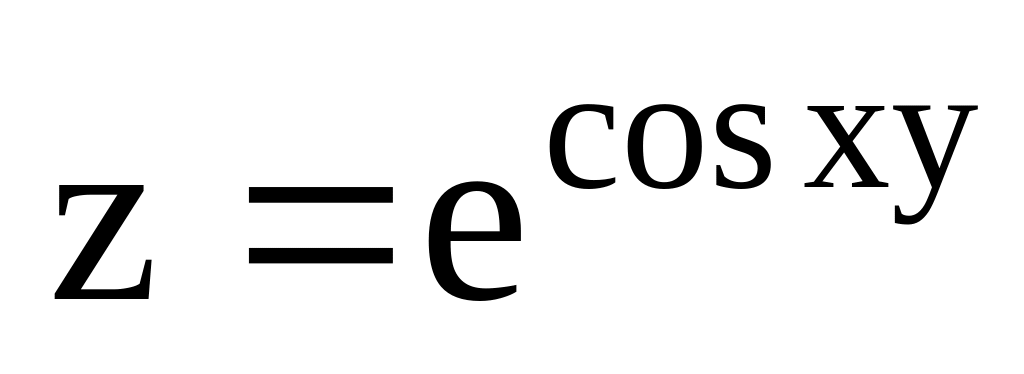
Визначити часткову похідну
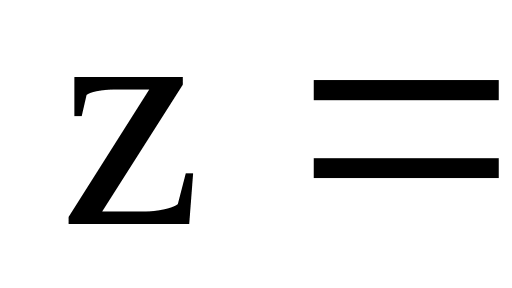
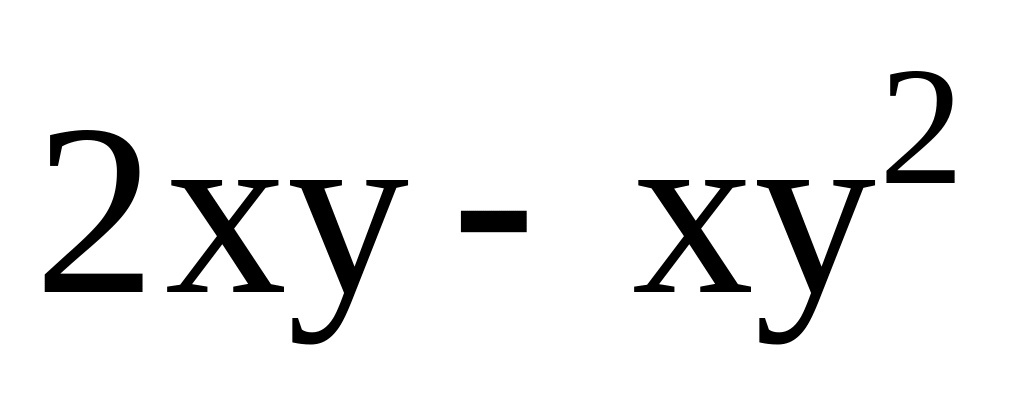
Визначити часткову похідну

Визначити часткову похідну z=lnsin(x2+y)
Визначити часткову похідну z=x2siny
Визначити часткову похідну z=ln(xy)
Визначити часткову похідну z=x2y2ex
Визначити часткову похідну

Визначити часткову похідну
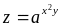
Визначити часткову похідну
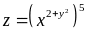
Визначити часткову похідну
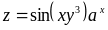
Визначити часткову похідну
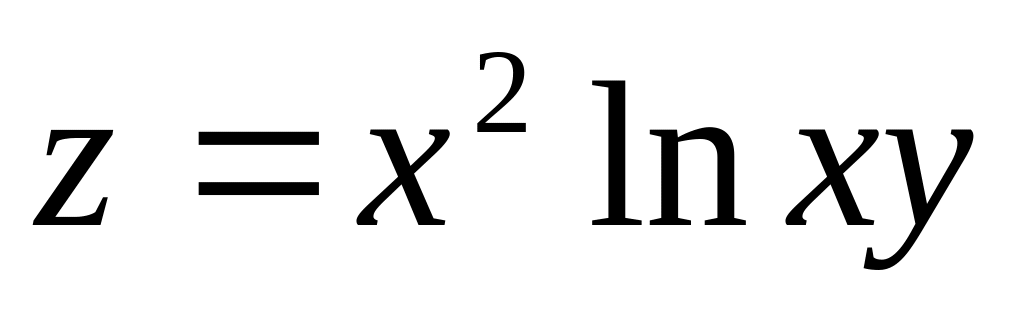
Визначити часткову похідну
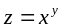
Визначити часткову похідну

Дискретна величина вважається заданою, якщо
Умова нормування випадкової величини має вигляд
Імовірність того, що неперервна випадкова величина матимє яке-небудь числове значення дорівнює
Прикладом неперервної випадкової величини є
Дискретною випадковою величиною є така випадкова величина, що
Прикладом дискретної випадкової величини є
Кількість можливих значень неперервної випадкової величини
Випадковою величиною називається величина
Математичне сподівання
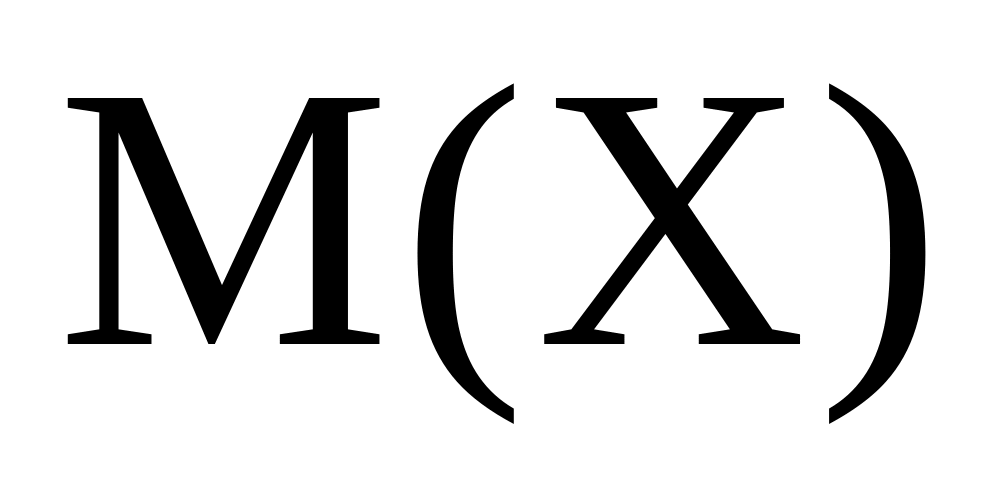 дискретної випадкової величини
визначається за формулою
дискретної випадкової величини
визначається за формулоюГустина імовірності
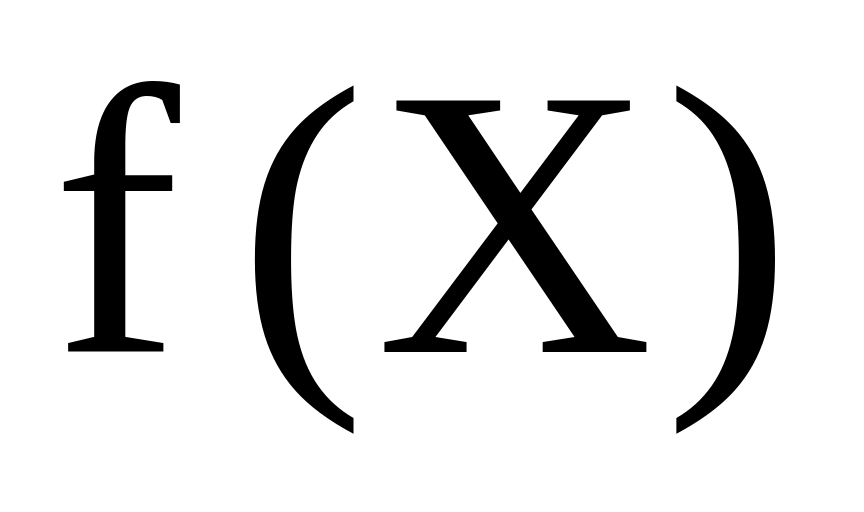 неперервної випадкової величини Х
визначається за формулою
неперервної випадкової величини Х
визначається за формулоюВ формулі
 функція
- це
функція
- цеНеперервною випадковою величиною є така випадкова величина, що
Імовірність того, що величина Х має яке-небудь числове значення в інтервалі від a до b визначається виразом
Задати закон розподілення дискретної випадкової величини – це означає
Середне квадратичне відхилення
 випадкової величини визначається за
формулою
випадкової величини визначається за
формулоюОдним із засобів завдання неперервної випадкової величини є
Функція розподілу
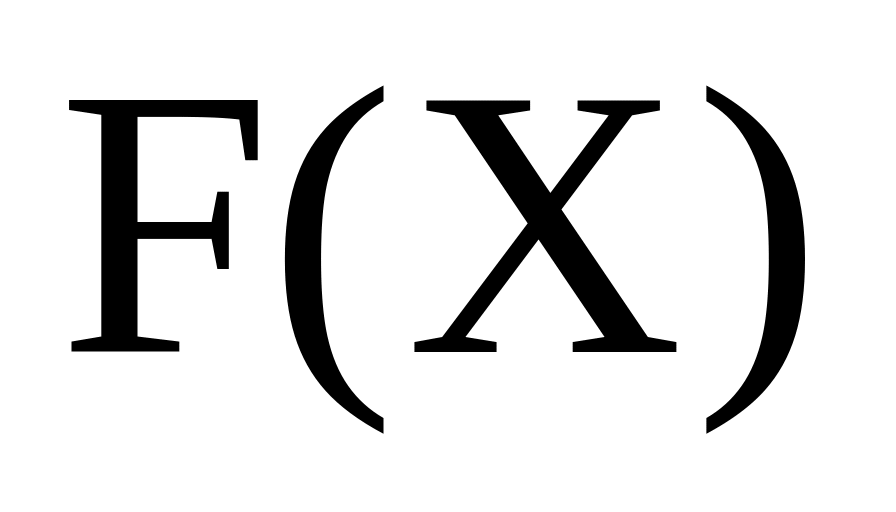 неперервної випадкової величини Х
визначається за формулою
неперервної випадкової величини Х
визначається за формулоюРозмірність дисперсії дорівнює
Неперервна випадкова величина приймає
Дисперсія дискретної випадкової величини визначається за формулою
Імовірність того, що неперервна випадкова величина Х має яке-небудь числове значення в інтервалі від a до b визначається виразом
Умова нормування для неперервної випадкової величини має вигляд
Імовірність того, що неперервна нормально розподілена випадкова величина приймає значення, що лежить у якому-небудь інтервалі:
Імовірність того, що неперервна випадкова величина приймає конкретне значення:
Густина імовірності f(x) безперервної випадкової величини Х може бути обчислена по формулі:
Умовою нормування неперервної випадкової величини є:
Функція розподілу F(x) неперервної випадкової величини Х, що має густина імовірності f(x), дорівнює:
Функція щільності імовірності f(x) може бути обчислена по формулі
Функція розподілу дорівнює імовірності того, що випадкова величина прийме значення, що лежить в інтервалі:
Функція розподілу безперервної випадкової величини лежить в інтервалі значень
Однієї з числових характеристик випадкової величини є
Математичне чекання М(х) безперервної випадкової величини Х обчислюється по формулі:
Для обчислення дисперсії випадкової величини Х може бути використана формула:
Для обчислення дисперсії безперервної випадкової величини Х може бути використана формула:
Середнє квадратичне відхилення безперервної випадкової величини Х може бути обчислене по формулі:
Якщо дисперсія безперервної випадкової величини Х дорівнює 0,04, то середнє квадратическое відхилення цієї величини дорівнює:
Якщо безперервна випадкова величина має нормальний розподіл, то її густина імовірності описується формулою:
У формулі
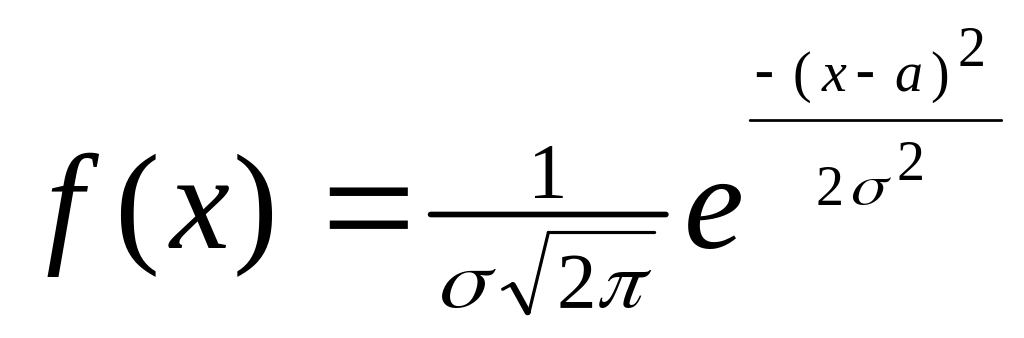 ,
що описує функцію щільності імовірності
нормально розподіленої випадкової
величини Х, константа а – це:
,
що описує функцію щільності імовірності
нормально розподіленої випадкової
величини Х, константа а – це:У формулі , що описує функцію щільності імовірності нормально розподіленої випадкової величини Х, константа s – це:
Графік функції щільності імовірності f(x) нормально розподіленої випадкової величини Х:
Графік функції щільності імовірності f(x) нормально розподіленої випадкової величини Х:
При будь-яких параметрах а і s площа під графіком функції щільності імовірності нормально розподіленої випадкової величини Х буде:
Якщо випадкова величина Х має нормальний розподіл, то імовірність її влучення в інтервал від х
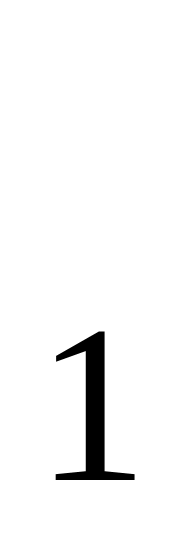 до х
до х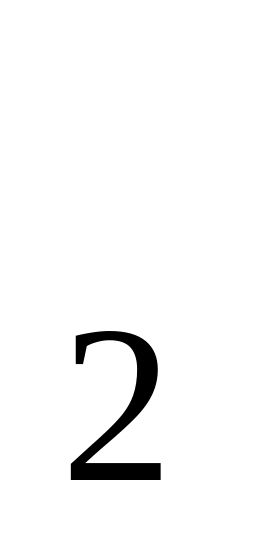 обчислюється по формулі:
обчислюється по формулі:Вибіркова сукупність - це
Для надійної оцінки статистичних характеристик ознаки генеральної сукупності обчислюють:
Оптимальна вибіркова оцінка середнього квадратичного відхилення
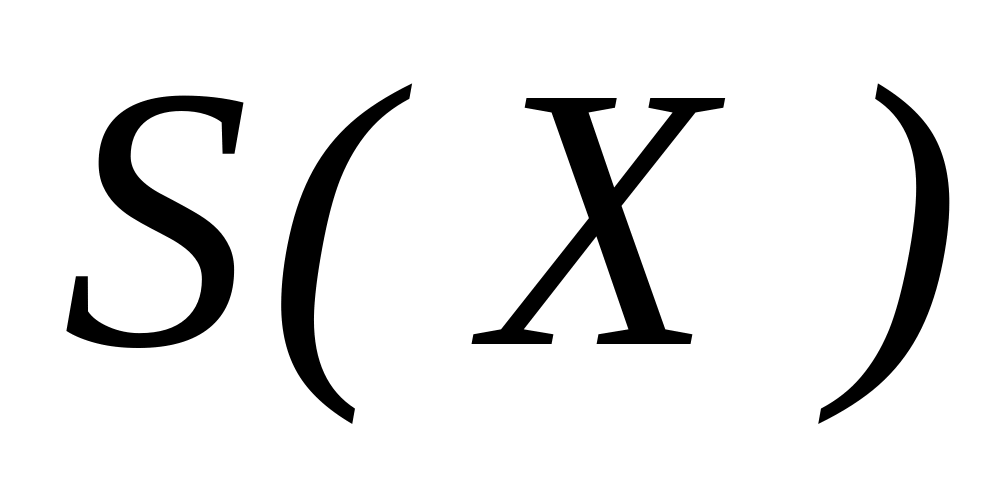 дорівнює:
дорівнює:Загальна площа прямокутників, що утворюють гістограму, дорівнює:
Помилка середнього обчислюється за формулою:
Рівень значущості
 дорівнює:
дорівнює:Границі надійного інтервалу для математичного сподівання нормально розподіленої випадкової величини
 є:
є:Чому дорівнює помилка середнього, якщо об’єм вибірки 16, а вибіркова дисперсія дорівнює 36?
Якщо рівень значущості дорівнює 0,001, то надійна імовірність дорівнює:
Гістограма густини відносної частоти попадання варіант у заданий інтервал є:
Рівень значущості при надійній імовірності 0,95 дорівнює:
Якщо надійну імовірність
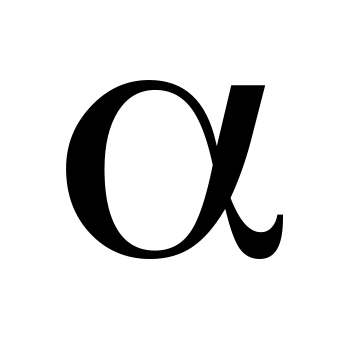 збільшити, то ширина надійного інтервалу
оцінки математичного сподівання
величини
за вибіркою:
збільшити, то ширина надійного інтервалу
оцінки математичного сподівання
величини
за вибіркою:Вибіркова оцінка середнього квадратичного відхилення величини дорівнює 2. Знайти вибіркову оцінку дисперсії, якщо об’єм вибірки дорівнює 9.
Границі надійного інтервалу:
Емпіричною оцінкою густини імовірності випадкової величини Х є:
Об’ємом вибірки називають:
Оптимальна точкова оцінка математичного сподівання ознаки генеральної сукупності за вибіркою (1;2;4;3;0) дорівнює:
Оцінки статистичних характеристик генеральної сукупності одержують при вивченні:
Рівень значущості дорівнює:
Вибіркою називається:
Значення коефіцієнта Стьюдента залежать від:
Знайти помилку середнього, якщо об’єм вибірки дорівнює 9, а вибіркова оцінка дисперсії дорівнює 36.
Об’ємом сукупності називають:
166. Відносна похибка дорівнює:
А)
![]()
В)
![]()
С)
![]()
D)
![]()
Е)
![]() ,
,
де
![]() - абсолютна похибка вимірювання,
- абсолютна похибка вимірювання,
![]() -
дійсне значення вимірюваної величини
-
дійсне значення вимірюваної величини
167. Відносна похибка це:
А) відношення дійсного значення до абсолютної похибки
В) відношення абсолютної похибки до дійсного значення
С) різниця між виміряним значенням і дійсним
D) вибірка дійсних значень випадкової величини
Е) середнє значення випадкової величини, знайдене по виборці
168. Точність вимірювання це:
А) величина, зворотна модулю абсолютної похибки
В) величина, прямо пропорційна відносній похибці
С) величина, зворотна модулю відносної похибки
D) сума методичною і інструментальною складових похибки вимірювання
Е) величина зворотна дійсному значенню дійсної величини
169. Систематичні похибки виникають в наслідок:
А) дії постійних деяких факторів
В) дії не постійних факторів
С) випадкової зміни температури навколишнього середовища
D) того, що всі вимірювані величини є випадковими
Е) наявність неконтрольованих факторів, які не можуть бути враховані наперед
170. Вимірювання вважаються за правильне якщо:
А) системна похибка рівна випадковій похибки
В) систематична похибка максимальна
С) систематична величина, прагне до нескінченності
D) систематична похибка мінімальна
Е) системна похибка рівна відносній похибки
171. Похибка вимірювання, що виникає унаслідок недосконалості методу вимірювань це:
А) суб'єктивна похибка
В) випадкова похибка
С) інструментальна похибка
D) методична похибка
Е) абсолютна похибка
172. Похибка, обумовлена технологічними засобами вимірювань, називається:
А) інструментальною похибкою
В) відносною похибкою
С) об'єктивною похибкою
D) систематичною похибкою
Е) методичною похибкою
173. Відношення абсолютної похибки до дійсного значення називається:
А) відносною похибкою
В) абсолютною похибкою
С) систематичною похибкою
D) методичною похибкою
Е) інструментальною похибкою
174. Дійсне значення вимірюваної величини обчислюють за формулою:
А)
![]()
В)
![]()
С)
![]()
D)
![]()
Е)
![]() ,
,
где n – число вимірювань
175. Величину абсолютної похибки обчислюють за формулою:
А)
![]()
В)
![]()
С)
![]()
D)
![]()
Е)
![]()
де
![]() - коефіцієнт Стьюдента;
- коефіцієнт Стьюдента;
![]() - довірча ймовірність
- довірча ймовірність
![]() ;
k
– число мір свободи, S
– вибіркова оцінка середнього
квадратичного відхилення величини
х.
;
k
– число мір свободи, S
– вибіркова оцінка середнього
квадратичного відхилення величини
х.
176. Клас точності приладу це:
А) абсолютна похибка, виражена у відсотках
В) приведена похибка, виражена у відсотках
С) відносна похибка, виражена у відсотках
D) величина зворотна точності вимірювання
Е) параметр, залежний виключно від похибки вимірювання
177. Якщо випадкова і інструментальна похибки одного порядку, то за дійсне значення береться:
А) абсолютна похибка
В) середнє генеральне
С) середнє вибіркове
D) різниця між абсолютною і відносною погрішностями
Е) будь-яке з їх значень
178. Малі значення систематичної похибки:
А) указують на правильність вимірювань
В) указують на те, що інструментальні похибки мінімальні
С) абсолютно не свідчать про правильність вимірювань
D) указують на відсутність неконтрольованих зовнішніх чинників
Е) приблизно рівні випадковим погрішностям
179. При вимірюванні кров'яного тиску людини випадкова похибка може бути пов'язана з:
А) систематичною похибкою
В) методикою вимірювання
С) інструментальною похибкою
D) неправильним положенням тіла
Е) дією постійних контрольованих факторів
