11. Какую скорость относительно воды должен сообщить мотор катеру, чтобы при скорости течения реки, равной 2м/с, катер двигался перпендикулярно к берегу со скоростью 3,5 м/с относительно берега?

Дано: катер – тело река – СО «К1» берег – СО «К2» V = 2 м/с (скорость реки относительно берега) V2 = 3,5 м/с (скорость катера относительно берега)	Решение: Согласно классическому закону сложения скоростей. При сложении векторов по правилу треугольника получаем следующий треугольник скоростей: β α т.к. полученный треугольник прямоугольный, используем теорему Пифагора , тогда м/с (модуль скорости) Чтобы найти направление скорости , определим сначала угол , а затем . . Ответ: катер относительно воды должен двигаться со скоростью 4 м/с под углом 60° к берегу против течения реки.
(скорость катера относительно реки)

12. Линейная скорость периферийных точек шлифовального камня не должна превышать 95 м/с. Определите наибольшее допустимое число оборотов в минуту для диска диаметром 30 см.

Дано: t = 1 мин = 60 с V = 95 м/с D = 30 см = 0,3 м	Решение: 1. 2. Ответ: 6051 оборотов в минуту

13. Длина минутной стрелки часов на Спасской башне Московского Кремля 2,5 м. Определите модуль и направление линейной скорости конца стрелки через каждые 15 мин в течение часа.

Дано: l = R = 3,5 м	Решение: → → A VA VД R B Д → VB → VC C Минутная стрелка один оборот по окружности совершает за 1 ч, поэтому период её обращения T = 1 ч = 3600 с. м/с Ответ: каждые 15 мин V = 6·10 м/с = const, направление скорости в каждой точке по касательной (см. рисунок).

14. Луна движется вокруг Земли на расстоянии 380000 км от неё, совершая один оборот за 27,3 сут. Вычислите центростремительное ускорение Луны.

Дано: R = 380000 км = = 380000000 м = = 3,8·108 м T = 27,3 сут. = = 27,3·24·3600 с = = 2358720 с 2,4·106 с	Решение: м/с

Задачи для самостоятельного решения

15. Группа ребят прошла сначала 200м на юг, а затем ещё 150м на восток. Найти геометрическим построением модуль и направление перемещения ребят, а также пройденный ими путь. (250м под углом37˚ на юго-восток, 35м)

16. Катер прошёл по озеру в направлении на запад 3км, а затем в северном направлении ещё 6км. Найти геометрическим построением модуль и направление перемещения катера, а также пройденный им путь. (6,7км под углом 64˚ на северо-запад, 9км)

17. Тело переместилось из точки с координатами X₀=1м, Y₀=2м в точку с координатами X=5м, Y=5м. Сделать чертёж, найти перемещение, его модуль и его проекции на оси координат. (5м, 4м, 3м)

18. Начальное положение материальной точки определяется координатами X₀=-1м, Y₀=1м. Определите координаты её конечного положения, постройте вектор перемещения точки и найдите его модуль, если S_x=4м, S_y=-3м. ( 3м, -2м, 5м)

19. Мяч упал с высоты 3м, отскочил от пола и был пойман на высоте 1м. Найти его путь и перемещение.(4м, 2м вниз)

20. Точка движется равномерно и прямолинейно в положительном направлении оси Ox. В начальный момент времени точка имела координату x₀ = -10 м. Найдите координату точки через 5 с от начала отсчёта времени, если модуль её скорости V= 2 м/с. Чему равен путь, пройденный точкой за это время? (0; 10 м)

21. Движение грузового автомобиля описывается уравнением x₁= –270+12t, а движение пешехода по обочине того же шоссе уравнением x₁= –1,5t. Сделать пояснительный рисунок (ось направить вправо), на котором указать положение автомобиля и пешехода в момент начала наблюдения. С какими скоростями и в каком направлении они двигались? Когда и где они встретились? (12 м/с, вправо; 1,5 м/с, влево; 20 с; -30 м)

22. Графики движения двух тел представлены на рисунке 1. Написать уравнения движения x=x(t). Что означают точки пересечения графиков с осями координат? (x₁=20+2t; x₂=-20+4t)

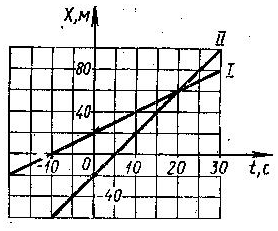
Рис.1

23. По графику изменения координаты материальной точки (рис.2) определить скорость движения и начертить график скорости. Какова скорость в см/с? в км/ч? (1000см/с; 36км/ч)

Рис.2

24. Скорость поезда за 20с уменьшилась с 72 до 54 км/ч. Написать формулу зависимости скорости от времени V_x(t) и построить график этой зависимости. (V_x = 20-0,25t)

25. По заданным на рисунке 3 графикам написать уравнения скорости тел V_x (t). Найти перемещения тел за первые две секунды движения. (V_xI=1,25t; V_xII=5+5t; V_xIII=20-4t; S_xI =2,5м; S_xII =20м; S_xIII =32м)

Рис.3

26. За какое время автомобиль, двигаясь из состояния покоя с ускорением 0,6 м/с², пройдёт 30 м? (10 c)

27. При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5с. Найти тормозной путь. (50 м)

28. Движения четырёх материальных точек заданы следующими уравнениями (соответственно): x₁=10t+0,4t²;x₂=2t-t²;x₃=-4t+2t²;x₄=-t-6t². Написать уравнение V_x=V_x (t) для каждой точки; построить графики этих зависимостей; описать движение каждой точки. (V_1x=10+0,8t; V_2x=2-2t; V_3x=-4+4t; V_4x=-1-12t)

29. Движения двух автомобилей по шоссе заданы уравнениями x₁=2t+0,2t² и x₂=80-4t. Описать картину движения; найти: а) время и место встречи автомобилей; б) расстояние между ними через 5 с от начала отсчёта времени; в) координату первого автомобиля в тот момент времени, когда второй находился в начале отсчёта. (а)10с; 40м; б)45м в)120м)

30. Снаряд зенитной пушки, выпущенный вертикально вверх со скоростью 800м/с, достиг цели через 6с. На какой высоте находился самолёт противника и, какова скорость снаряда при достижении цели? (4620м, 740м/с)

31. Камень, упав с обрыва, достиг поверхности воды через 2с. Чему равна высота обрыва. Найдите модуль конечной скорости камня. (20м, 20м/с)

32. Эскалатор метро движется со скоростью 0,75 м/с. Найти время, за которое пассажир переместится на 20 м относительно Земли, если он сам идёт в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчёта, связанной с эскалатором. (20 с)

33. Два поезда движутся навстречу друг другу со скоростями 72 и 54 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 14 с. Какова длина второго поезда? (490 м)

34. Лодка движется перпендикулярно к течению воды со скоростью 4,0 м/с. С какой скоростью движется лодка относительно берега, если скорость течения воды равна 3,0 м/с? (5 м/с)

35. Какова скорость точек земной поверхности на широте Санкт- Петербурга (60°) при суточном вращении Земли? (230 м/с)

36. Скорость точек экватора Солнца при его вращении вокруг своей оси равна 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек экватора. (25,3 суток; 5,7 мм/с²)

37. С какой скоростью автомобиль должен проходить середину выпуклого моста радиусом 40 м, чтобы центростремительное ускорение равнялось ускорению свободного падения? (20 м/с)

38. По данным таблицы составьте задачи и решите их.

№	R, м	T, с		, Гц	V, м/с
1	0,5	2	?	?	?
2	0,1	?	?	?	10
3	?	?	10	?	5
4	2,0	?	?	0,25	?
5	?	0,02	?	?	30