
Практическая работа №2 «Тригонометрические функции»
ЦЕЛЬ РАБОТЫ:
Корректировать знания, умения и навыки в теме: «Тригонометрические функции».
Закрепить и систематизировать знания по теме.
Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: калькуляторы, таблицы по теме «Тригонометрия».
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1.Изучить условие заданий для практической работы и решить их.
2.Оформить отчет о работе.
-
Вариант
1. Выразите величину угла
2.Отметьте на единичной окружности точку
 .
Покажите на чертеже значения
.
Покажите на чертеже значения
 и
и
 ,
если
,
если
 равно
равно3.Определите знак числа:
4.Вычислите:
а) в радианной мере:
б) в градусной мере:
А)
Б)
А)
Б)
1



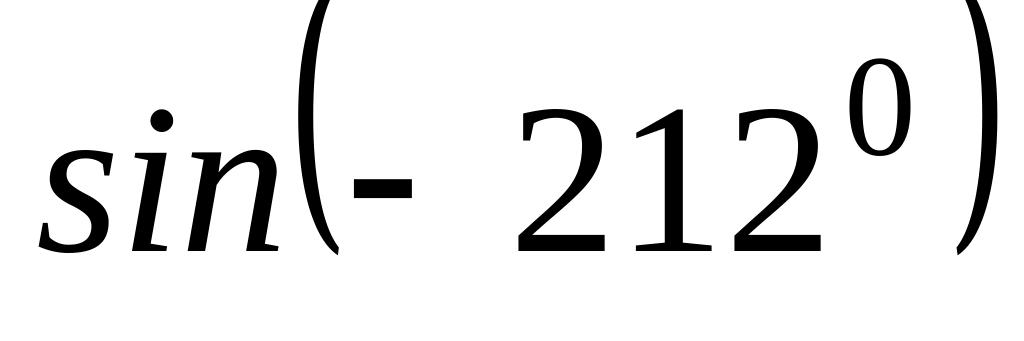


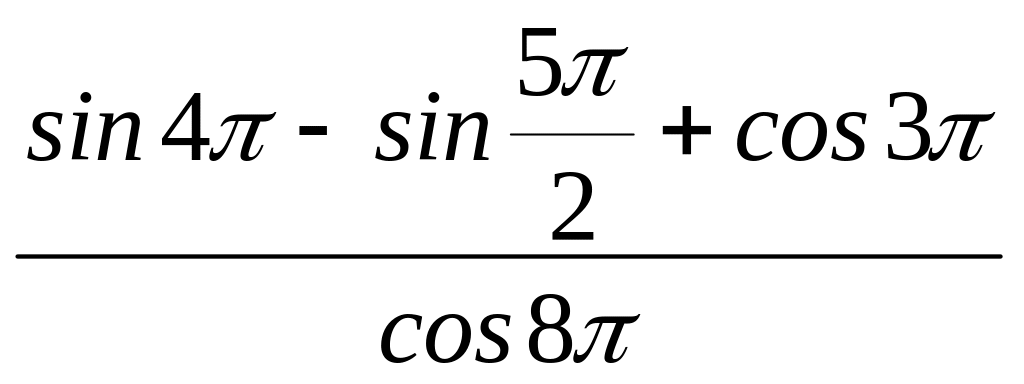
2
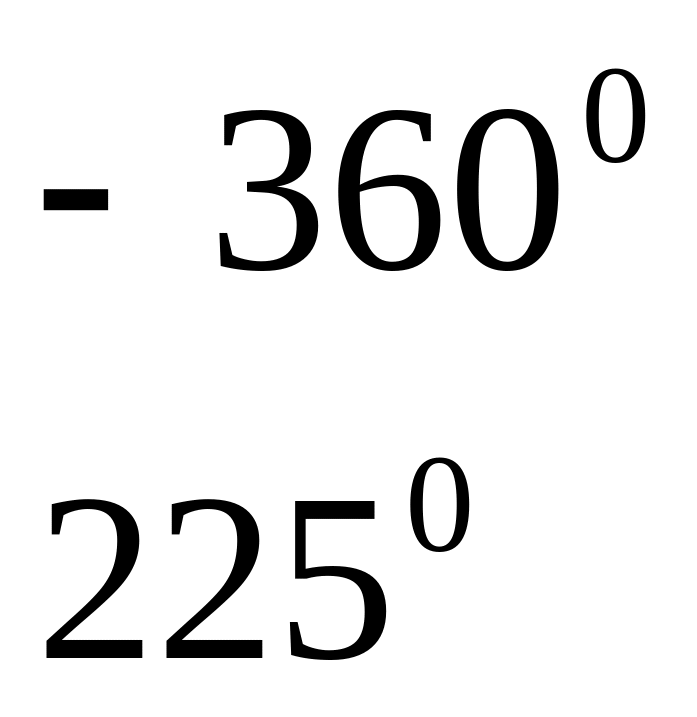

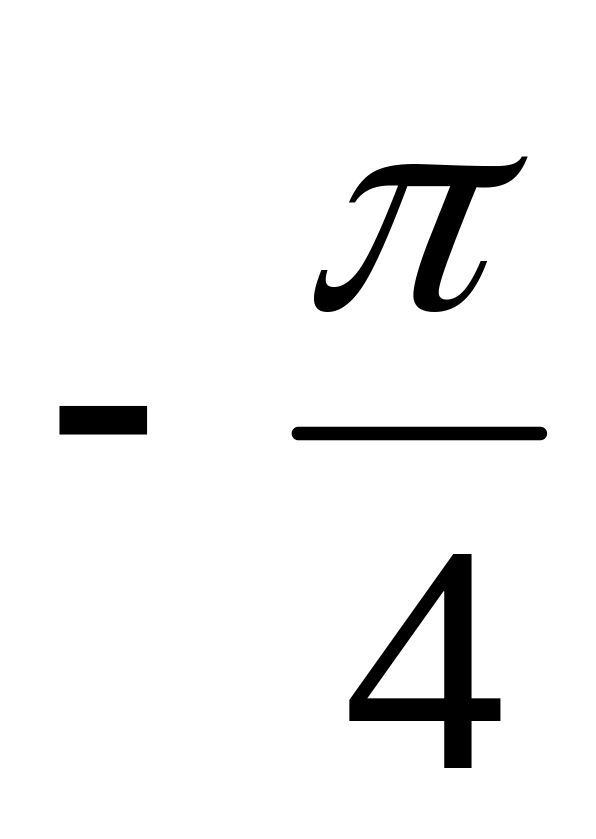
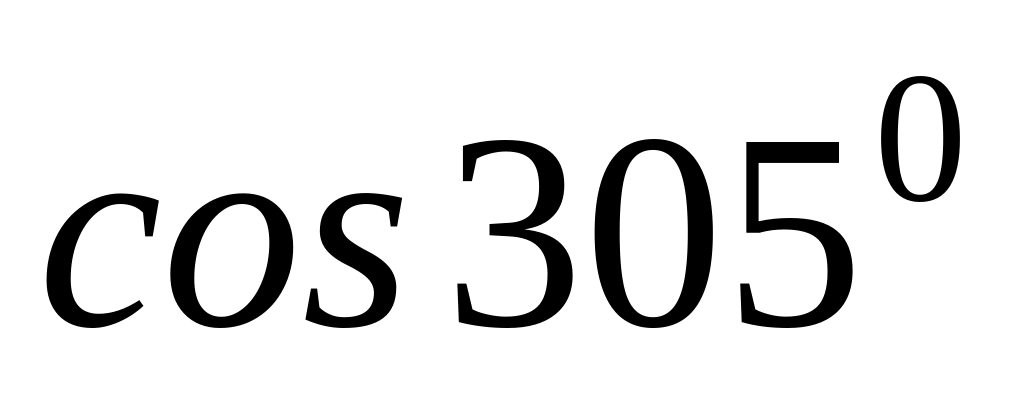
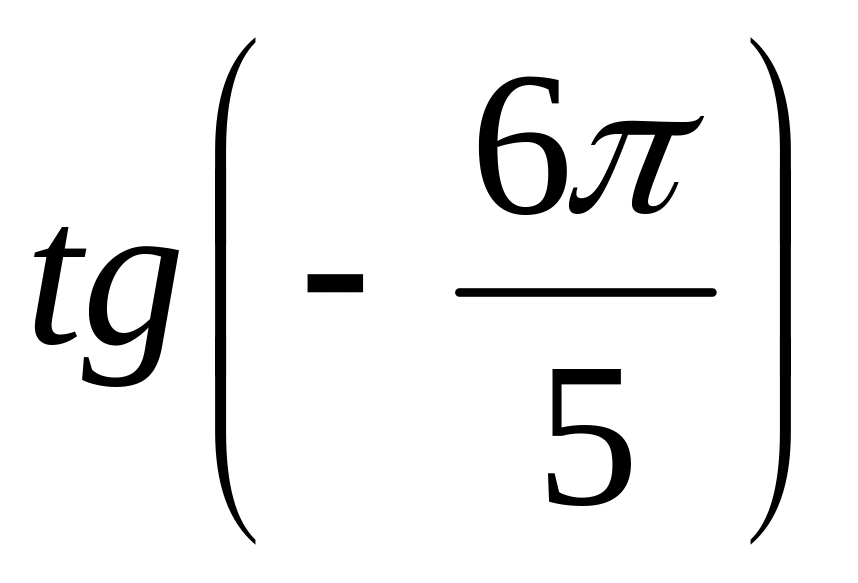
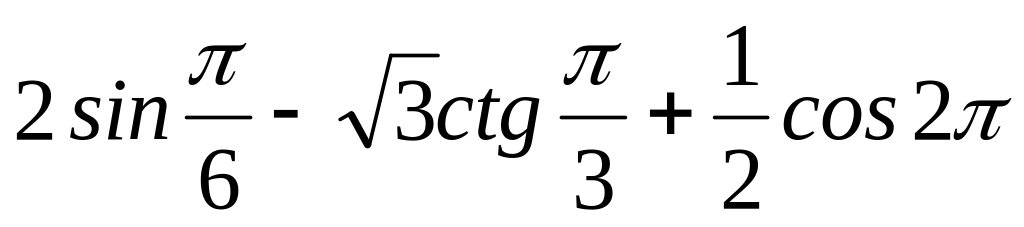

3
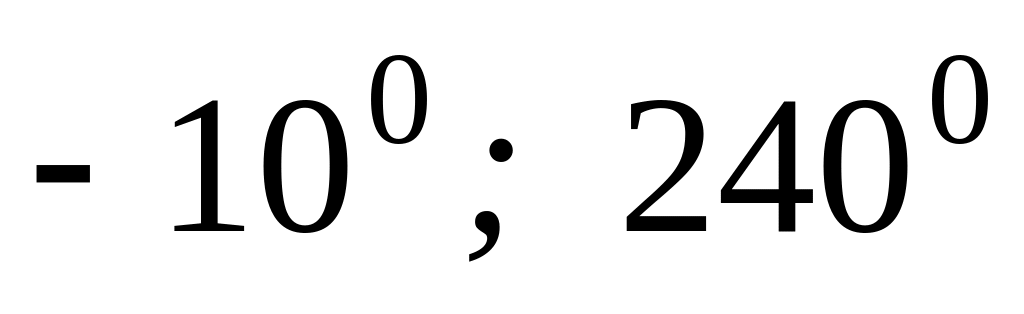
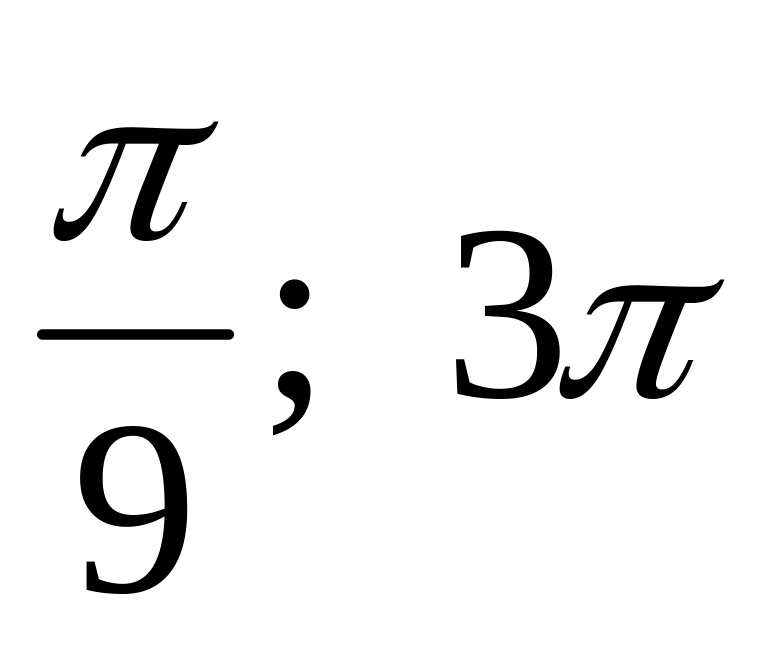
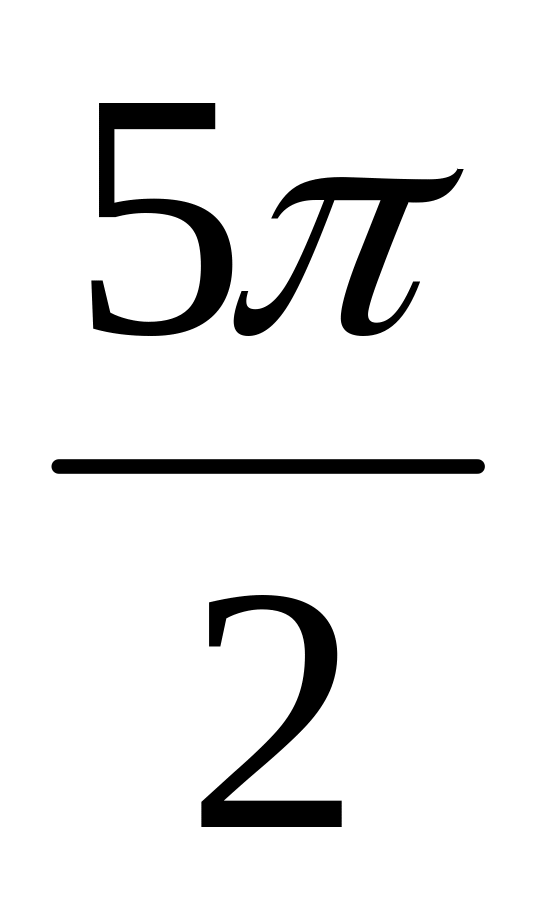
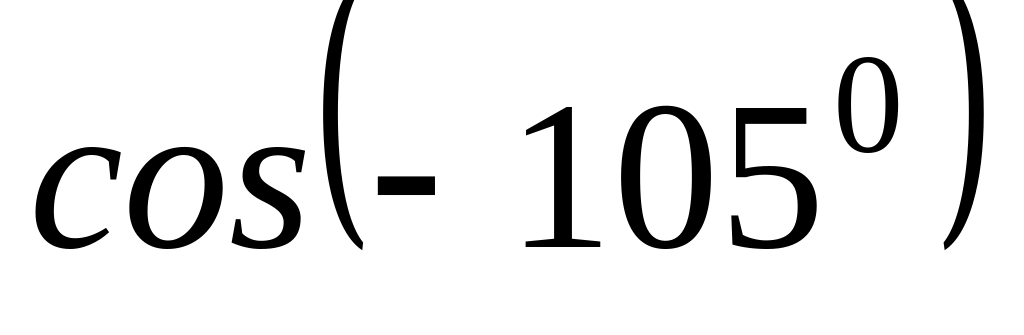
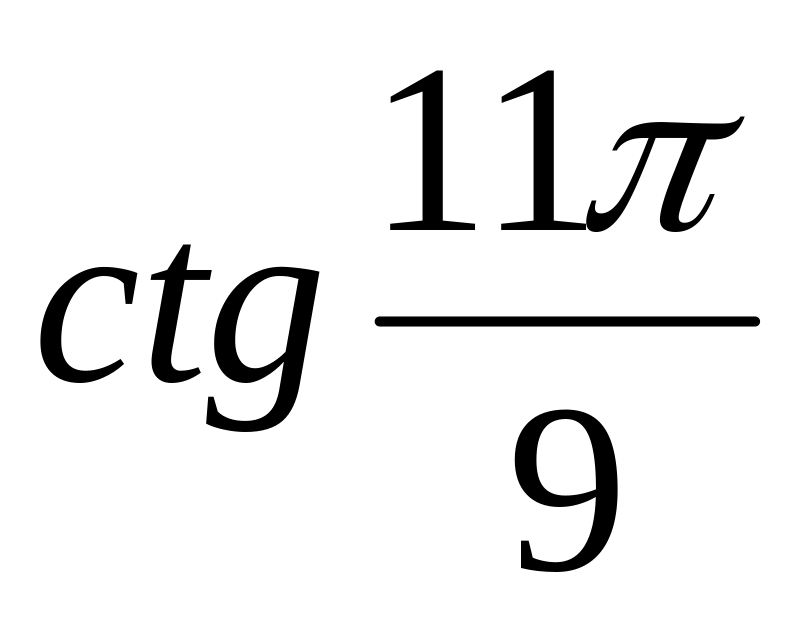
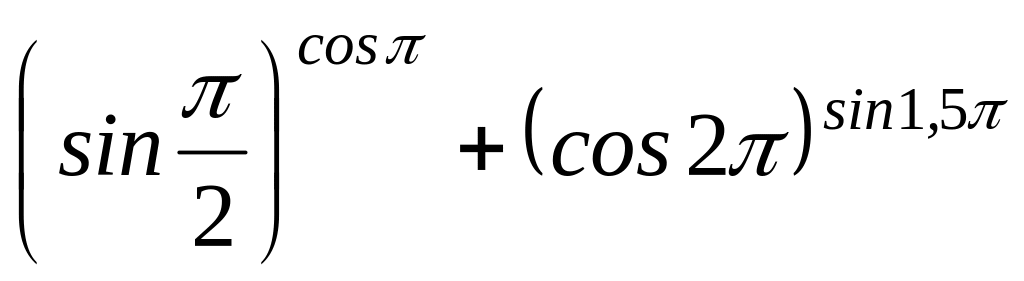

4


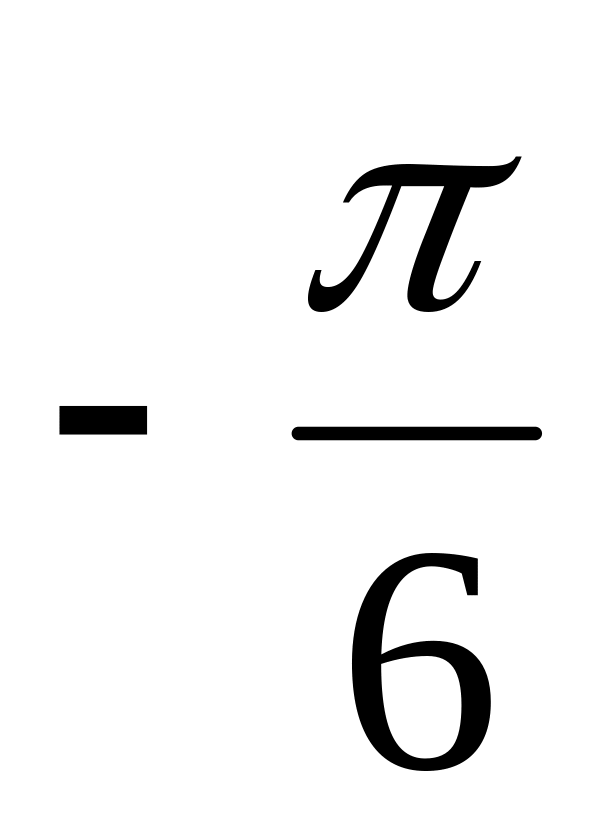
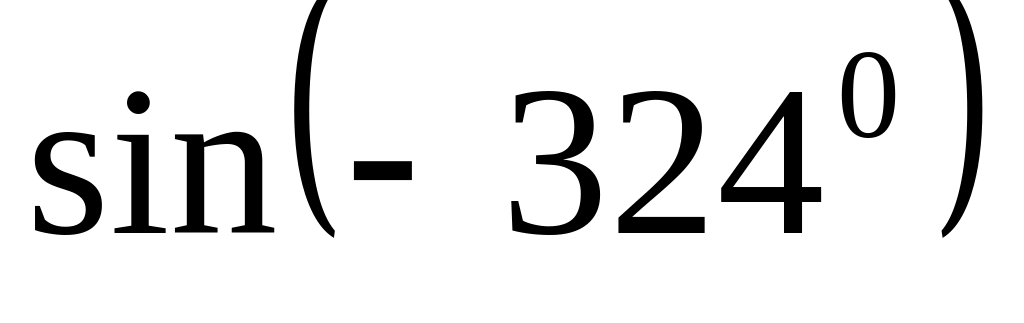



5
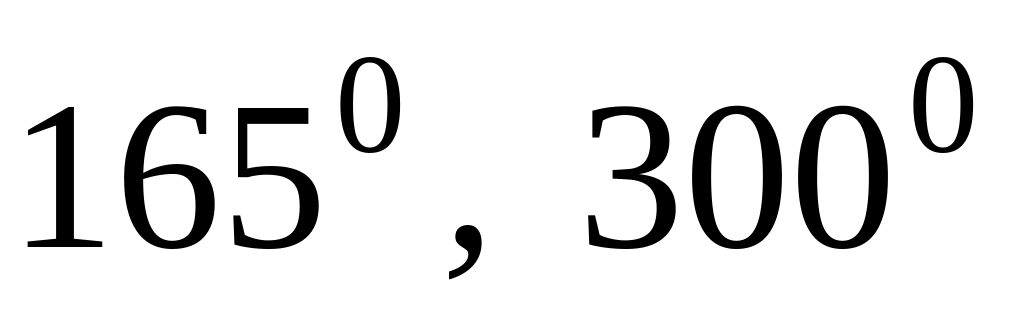
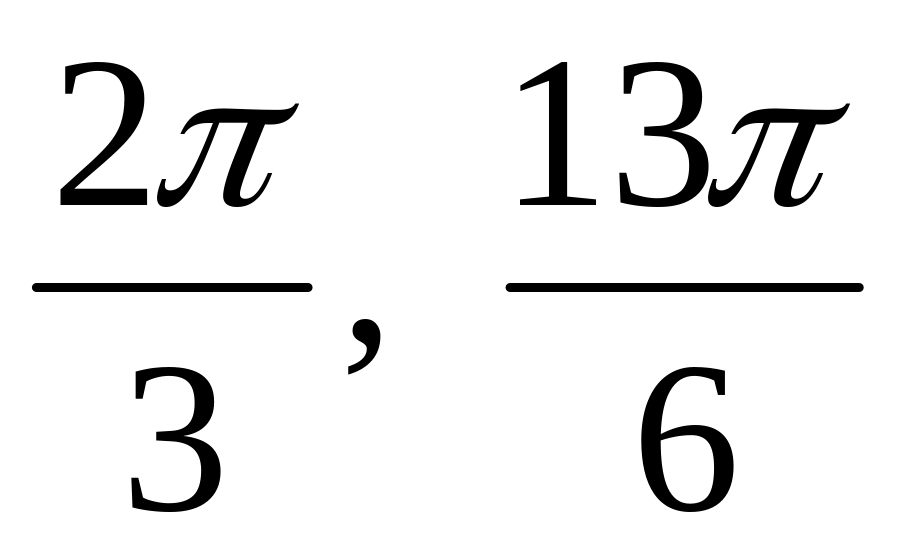
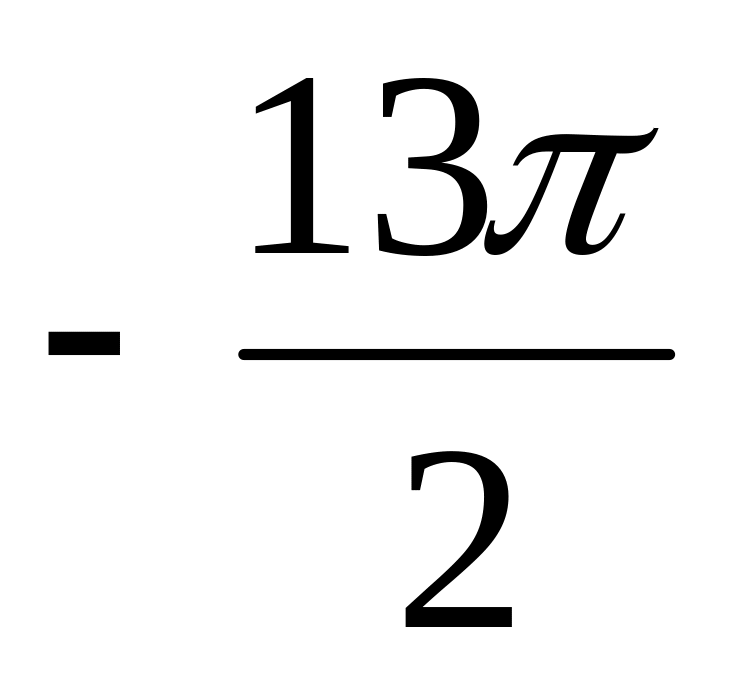
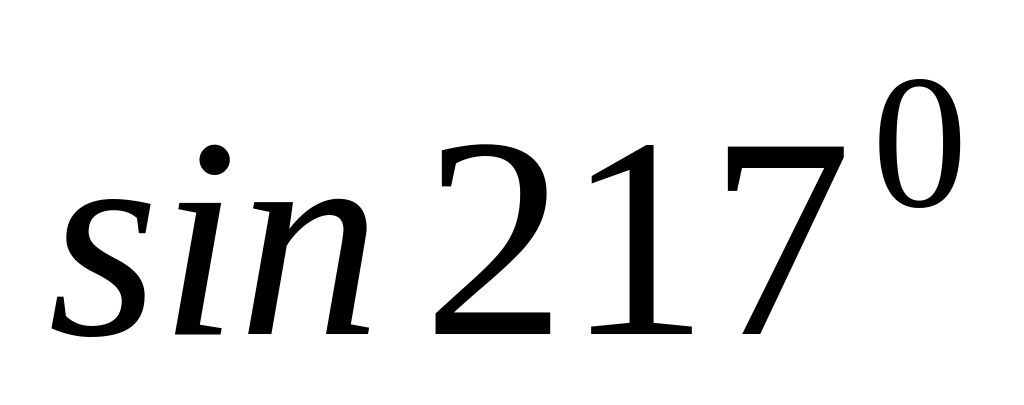
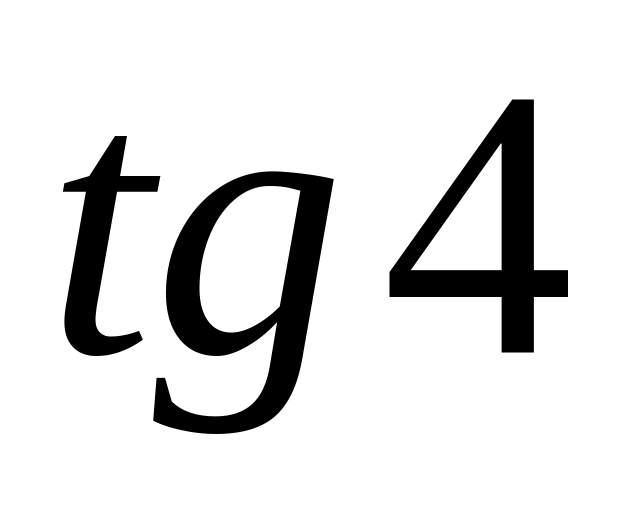

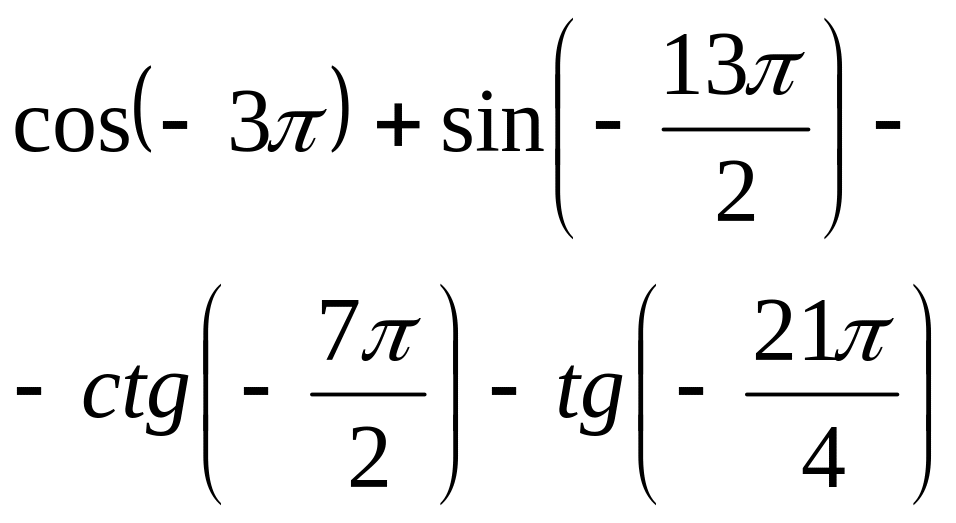
6
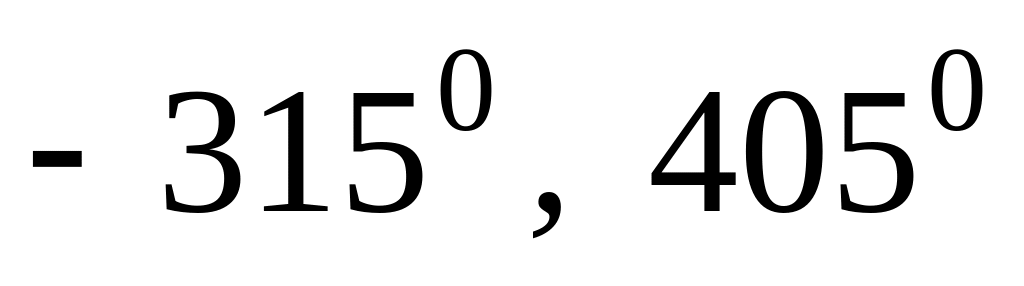
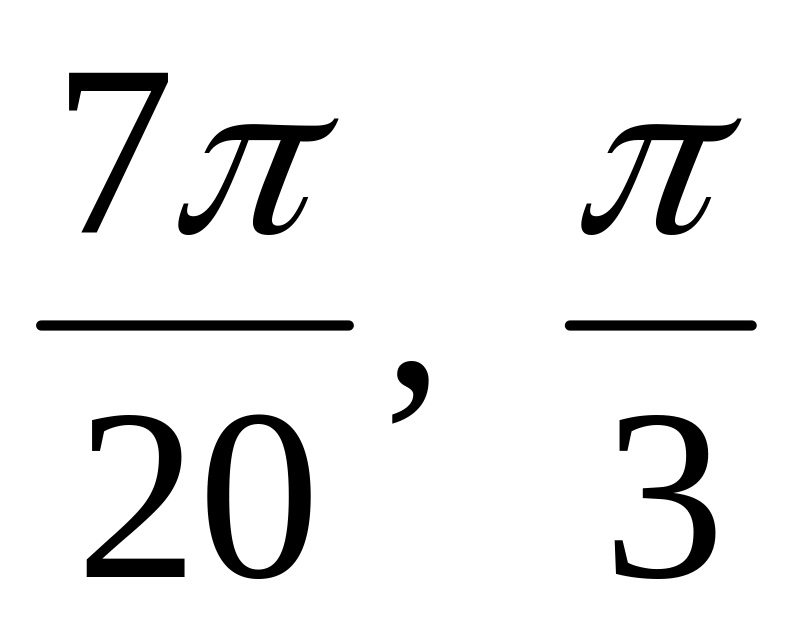
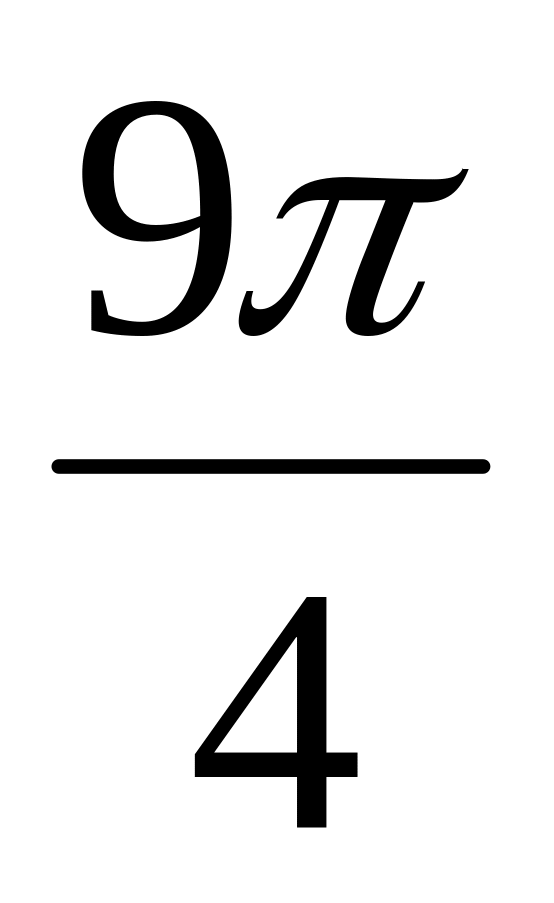

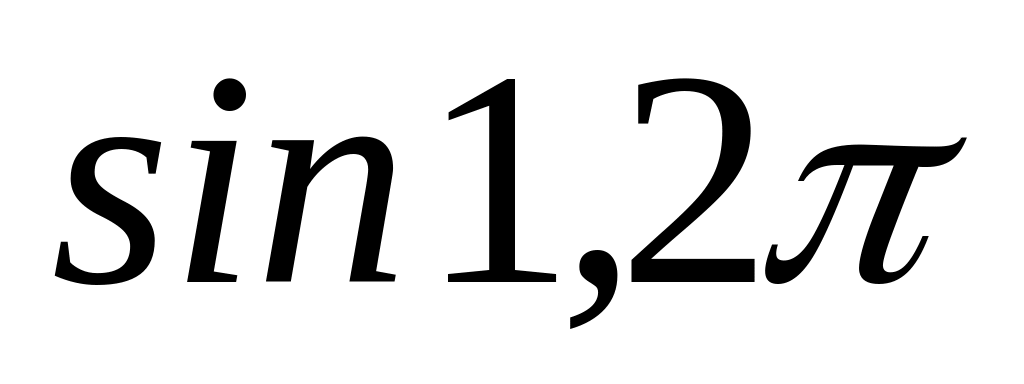
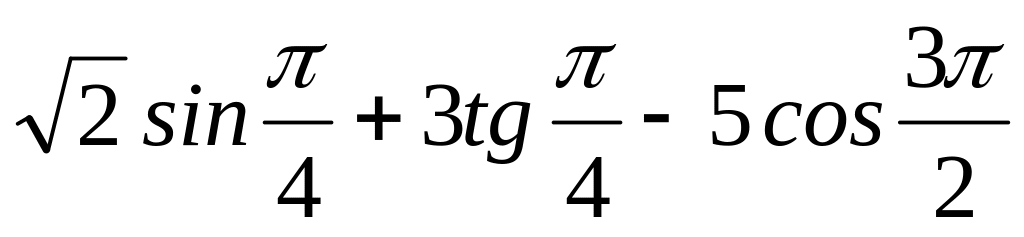
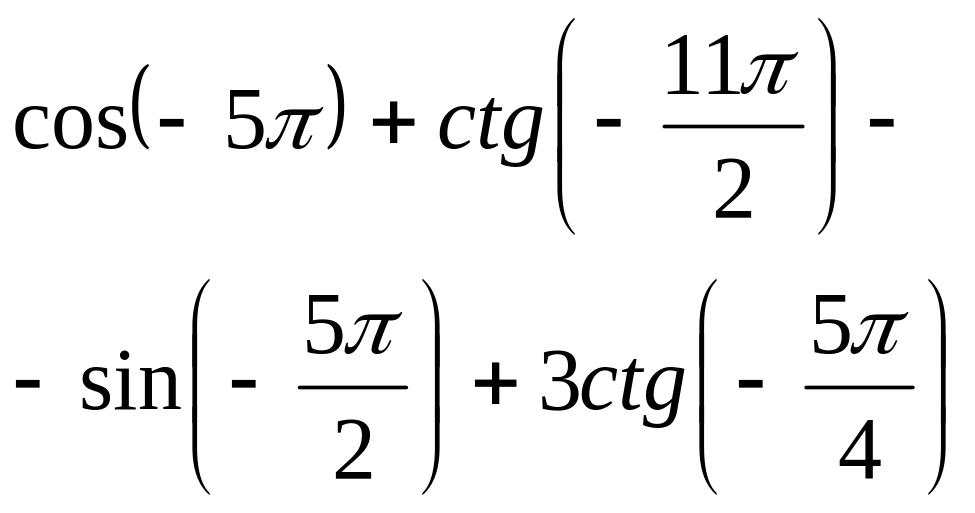
Вариант
5.Найдите значение тригонометрической функций
6.Преобразуйте выражения:
1
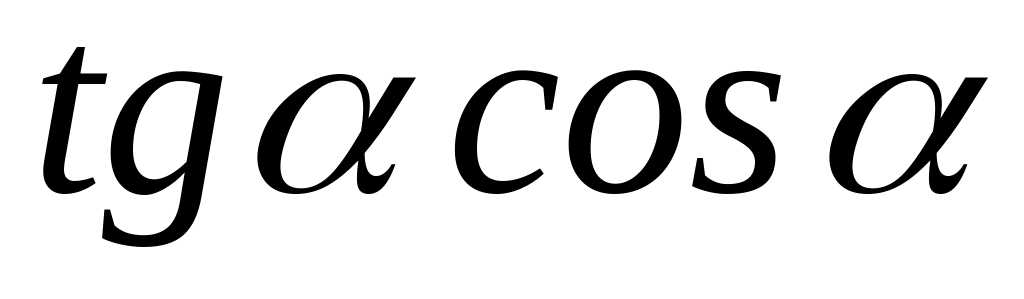
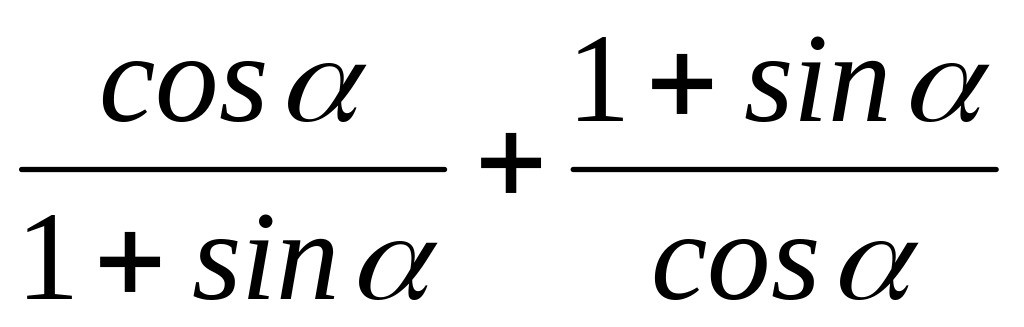
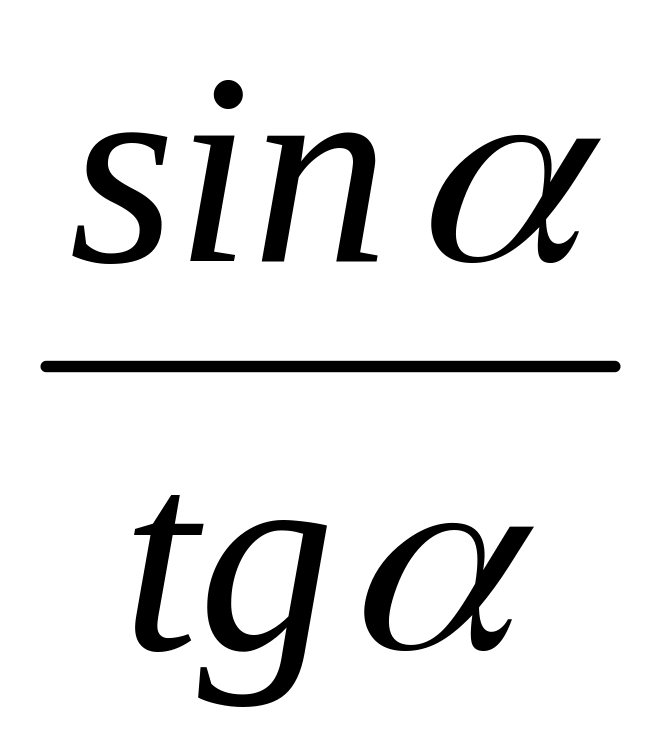
2
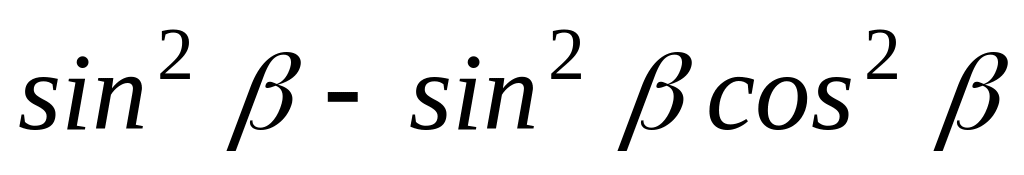
3
4
5
6
Тренировочный раздел
Тема: «Основные тригонометрические формулы»
Основное тригонометрическое тождество
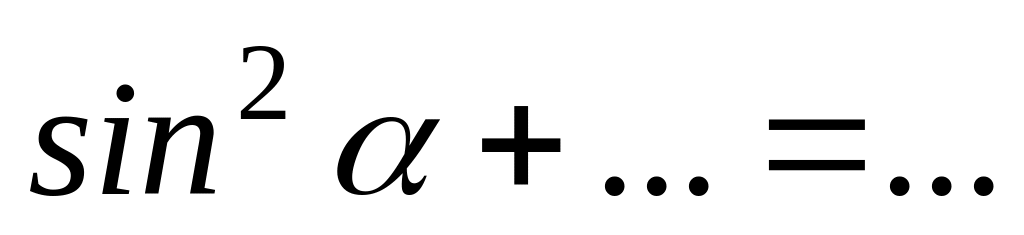 выполняется при любых значениях
.
выполняется при любых значениях
.Упростите выражения: а)
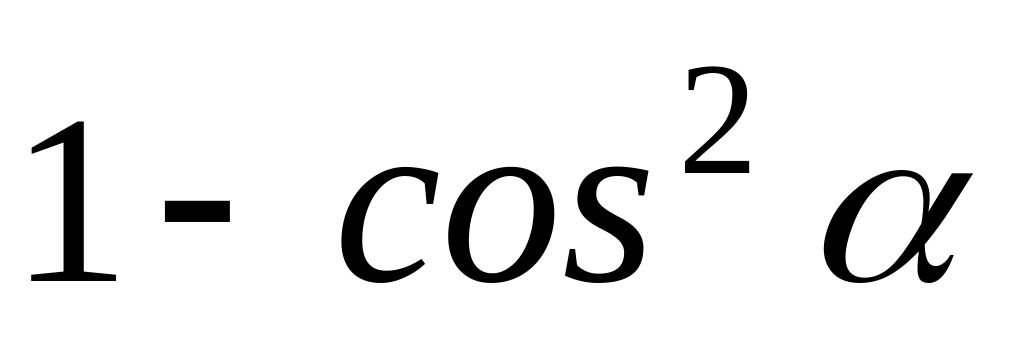 ;
б)
;
б)
 .
.Следствием из основного тригонометрического тождества является формула, выражающая через :
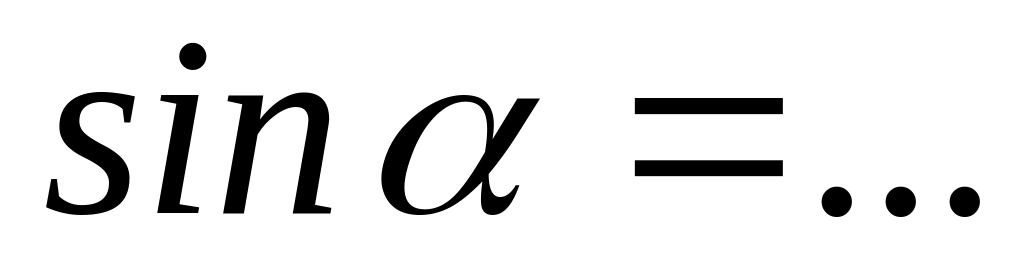 .
., если известно, что
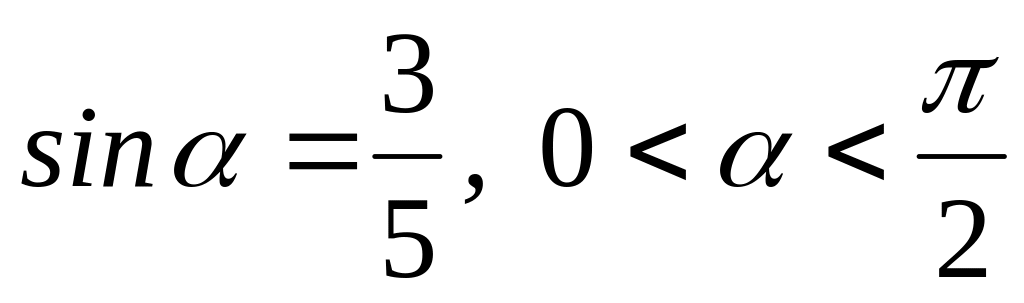 .
.Тангенсом угла называется отношение ... угла к его ...:
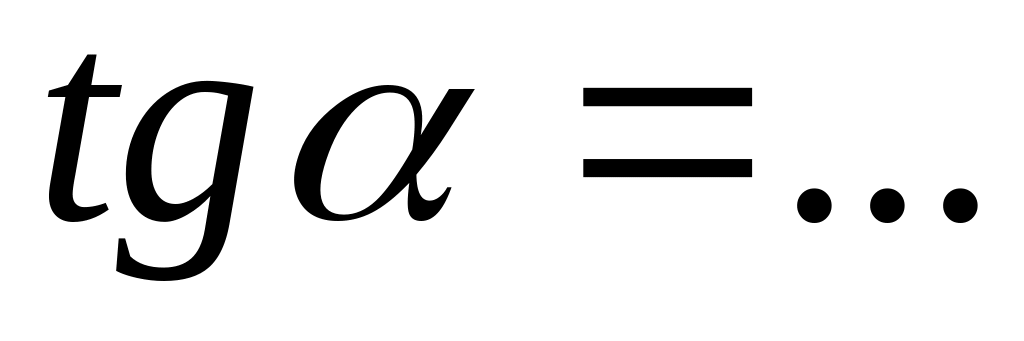 .
.Из определения тангенса и котангенса следует:
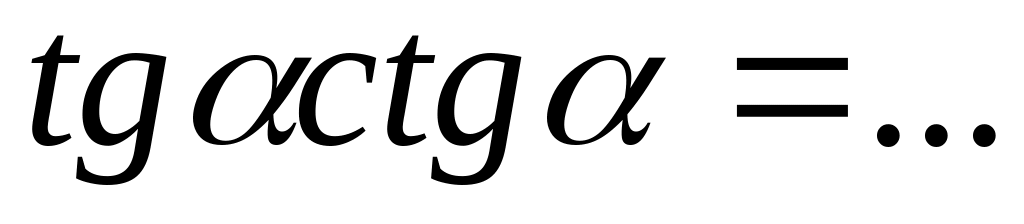 .
.Соотношение между тангенсом и косинусом одного и того же угла
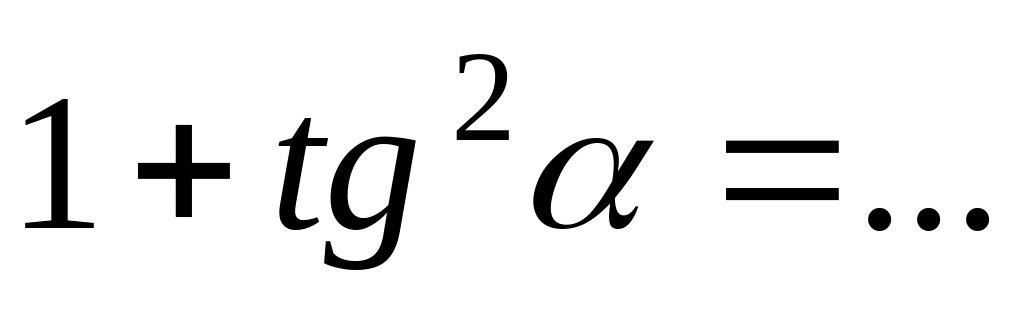
Формула
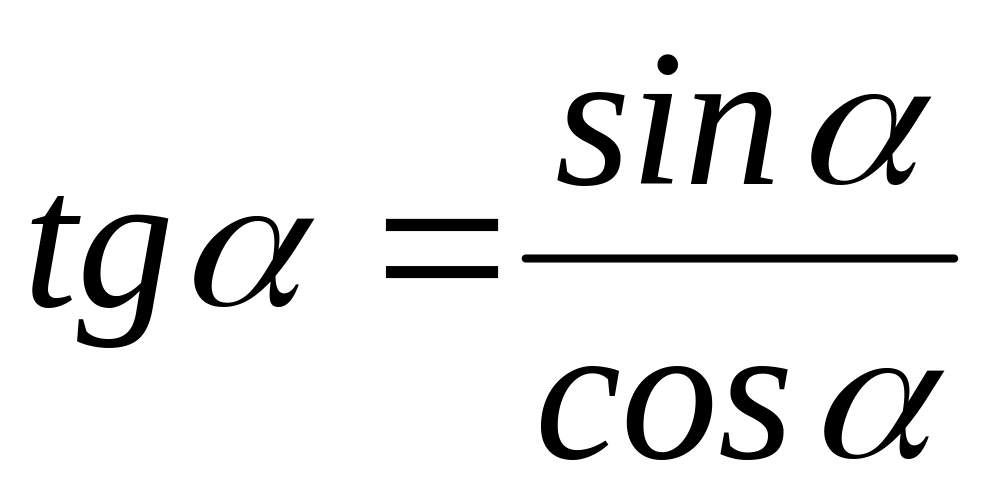
а); б) ; в).
Упростите: а); б)
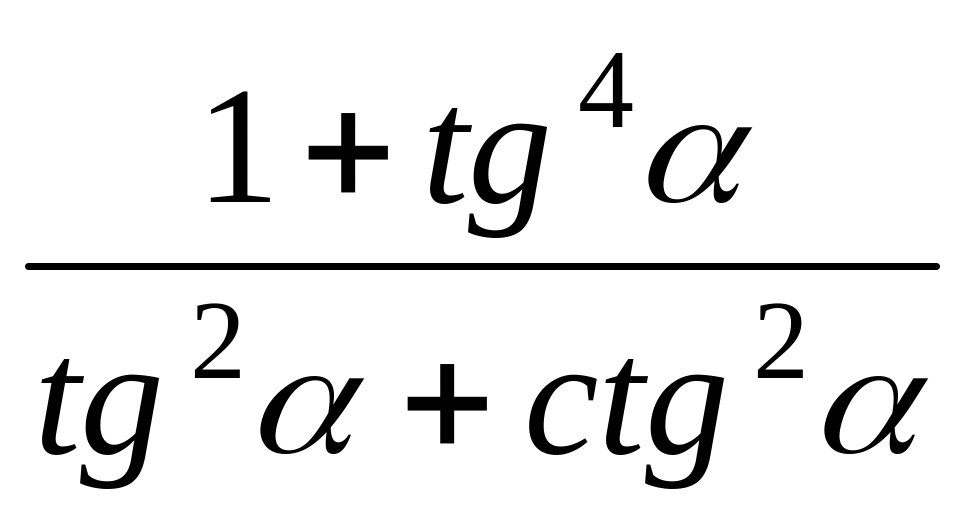 .
.
Докажите тождество:
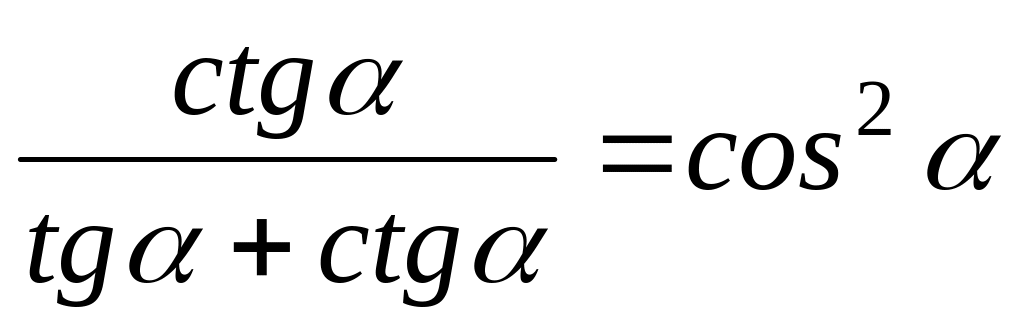 .
.
Тема: «Формулы приведения»
З
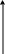 наки
тригонометрических функций:
наки
тригонометрических функций:
 y
y
y
y
II I II I

 x
x
x
x
0 0
III IV III IV
знаки синуса знаки тангенса
Четность и нечетность тригонометрических функций:
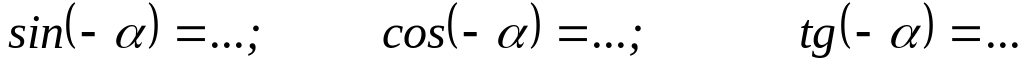 .
.
Вывод: четной функцией является ....
Найдите значения выражений: а)
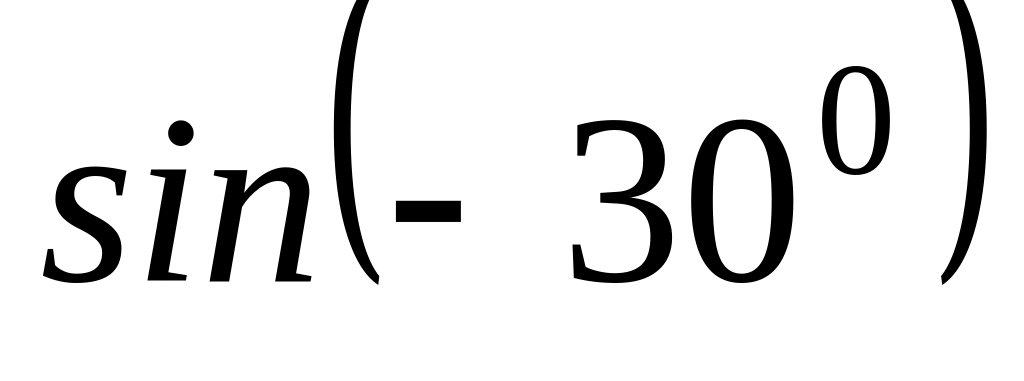 ;
б)
;
б)
 ;
в)
;
в)
 .
.Тригонометрические функции углов вида
 могут быть выражены через функции угла
с помощью формул приведения:
могут быть выражены через функции угла
с помощью формул приведения:
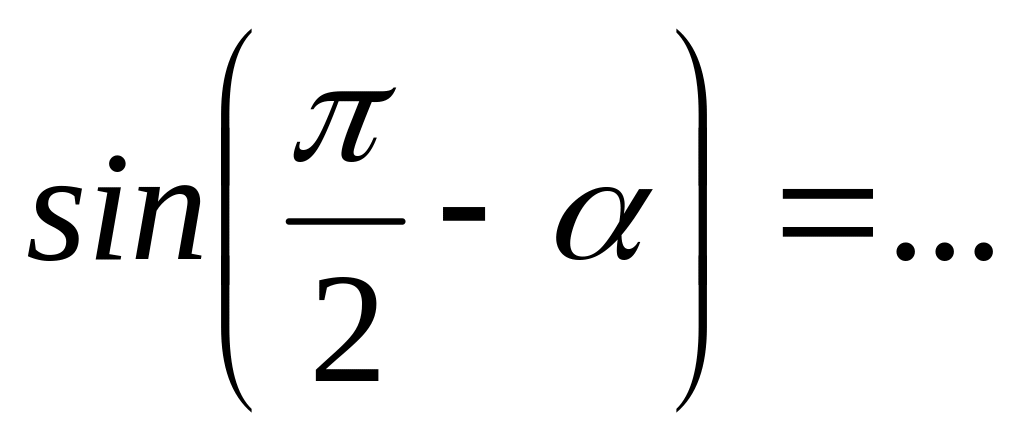 ;
;
 ;
;
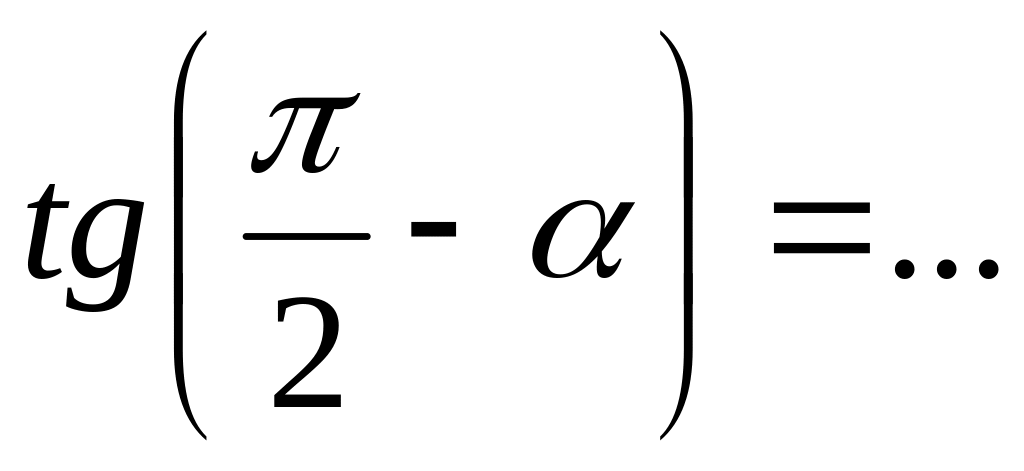 ;
;
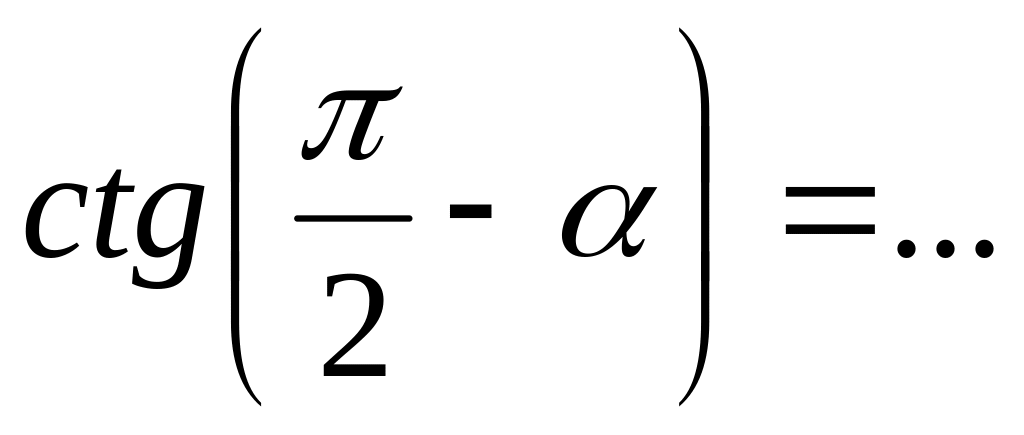 ;
;
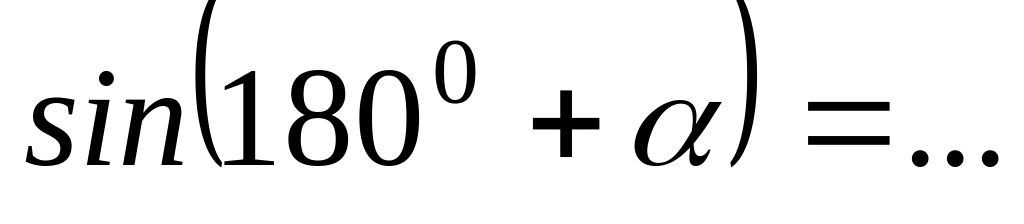 ;
;
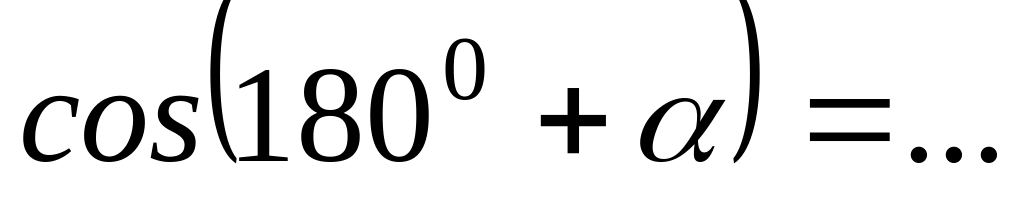 ;
;
 ;
;
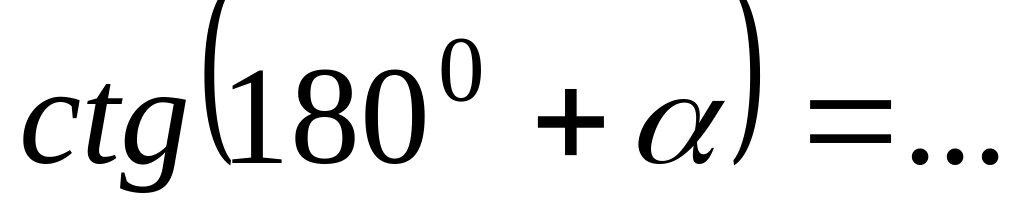 ;
;
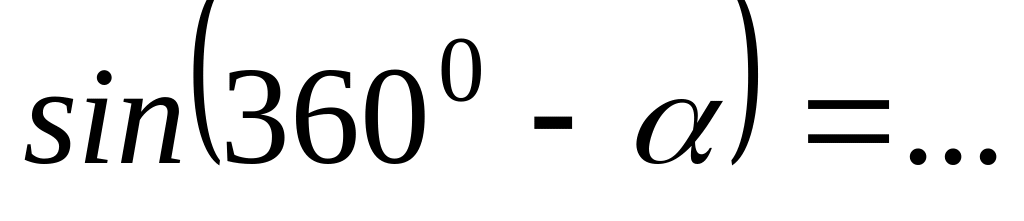 ;
;
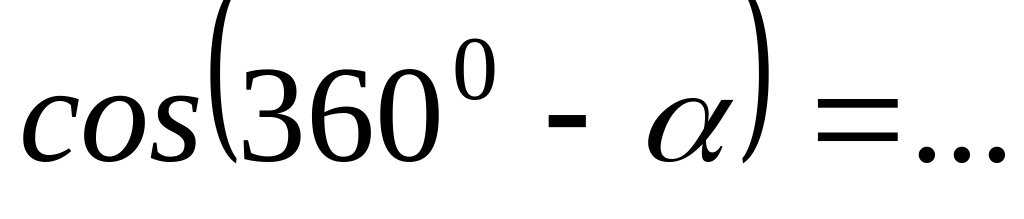 ;
;
 ;
;
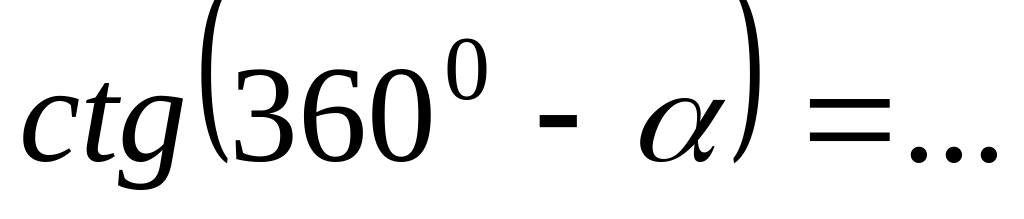 ;
;
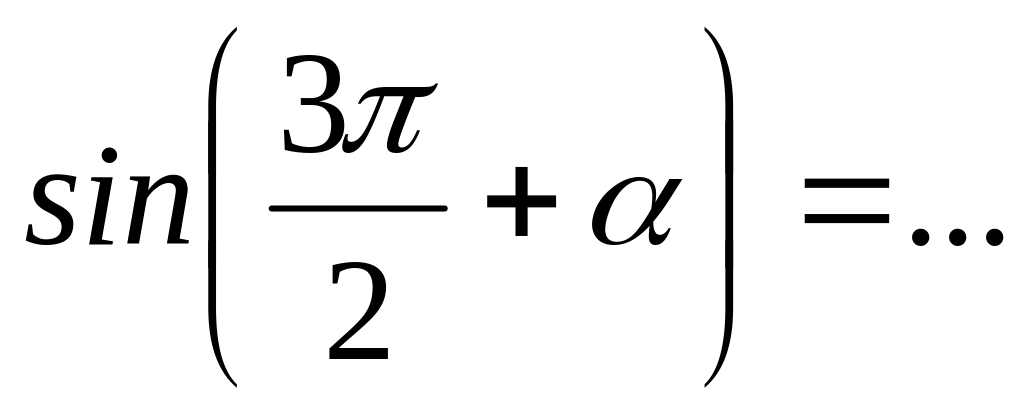 ;
;
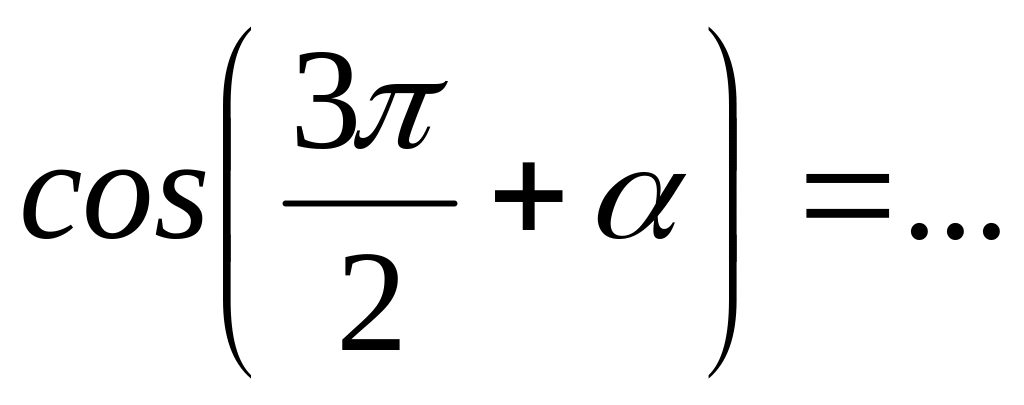 ;
;
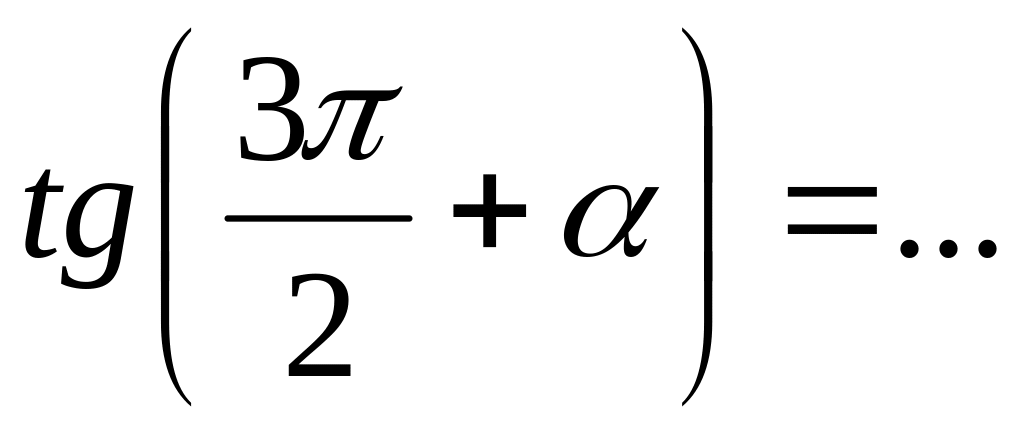 ;
;
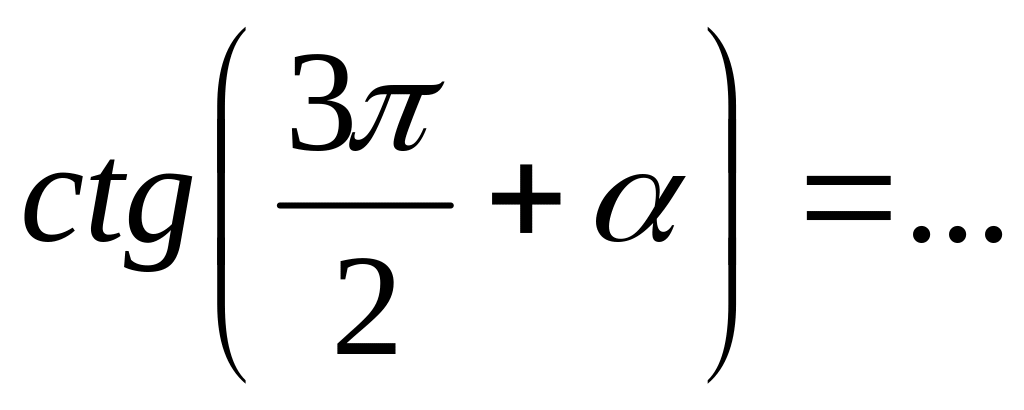 .
.Вычислите: а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
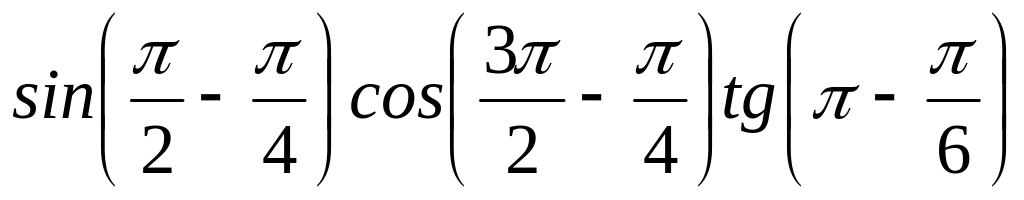 ;
;
д)
![]() .
.
Тема: «Формулы сложения»
Для любых
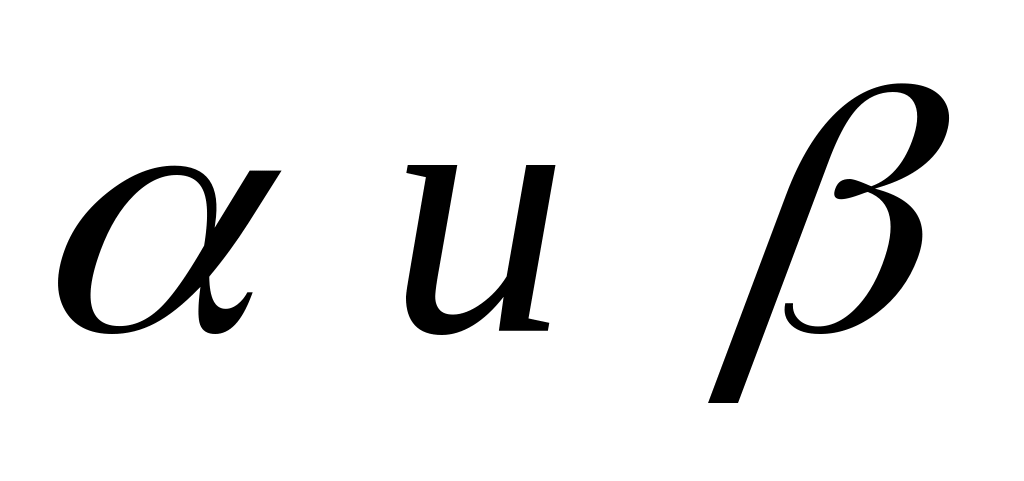 справедливы равенства: а)
справедливы равенства: а)
 ;
;
б)
![]() ;
в)
;
в)
![]() .
.
Вычислите: а)
 ;
б)
;
б)
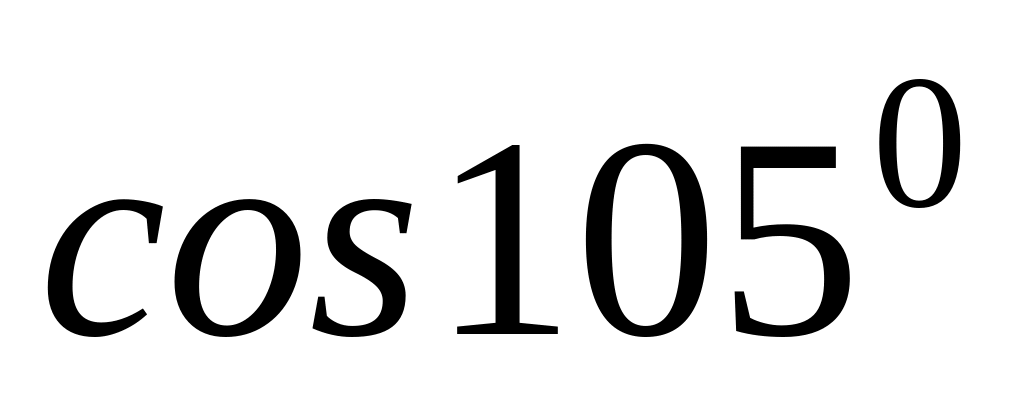 .
.Упростите: а)
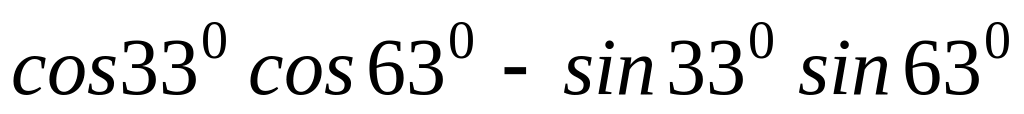 ;
б)
;
б)
 ;
;
в)
![]() ;
г)
;
г)
![]() .
.
Тема: «Формулы двойного угла»
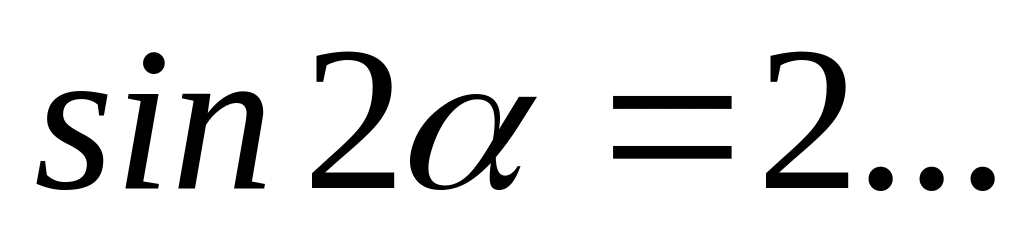 .
.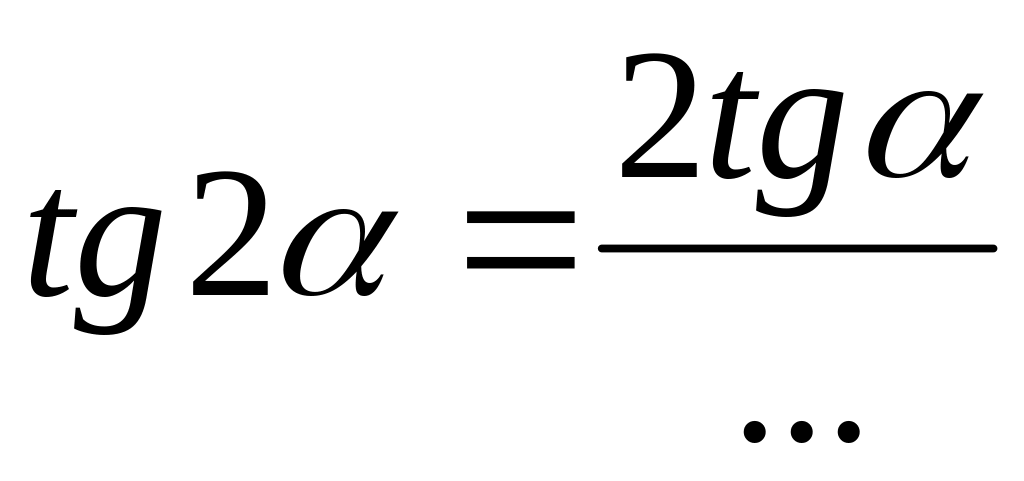 .
.Упростите: а)
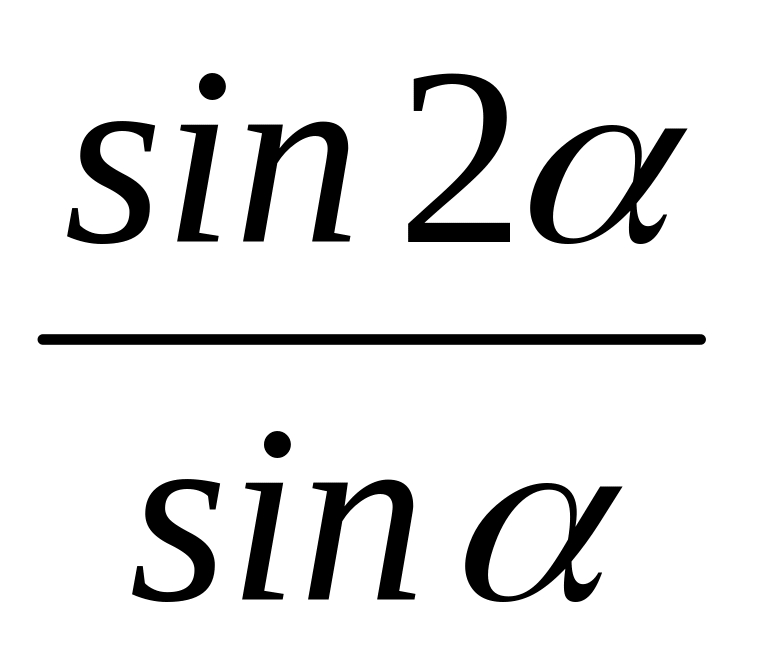 ;
б)
;
б)
 .
.Вычислите: а)
 ;
б)
;
б)
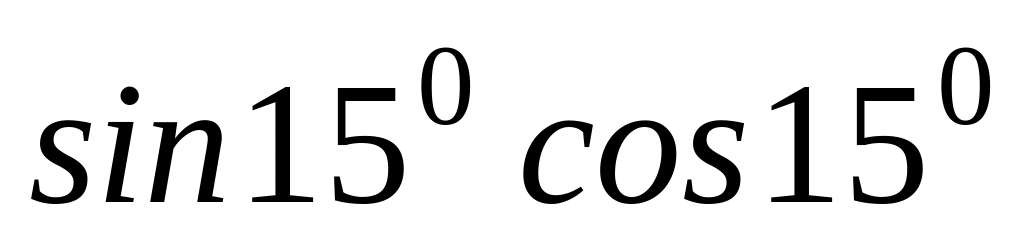 ;
в)
;
в)
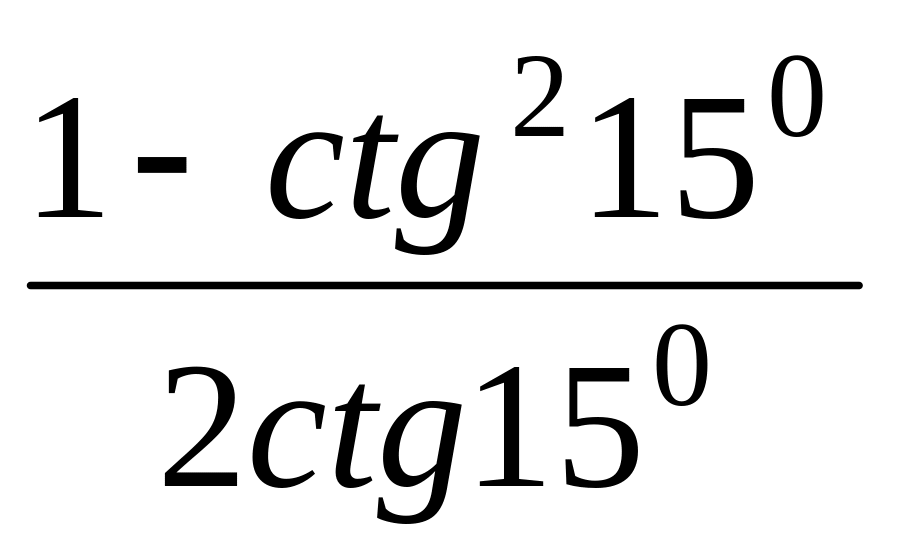 .
.
Тема: «Формулы суммы и разности тригонометрических функций»
Формула суммы синусов двух углов:
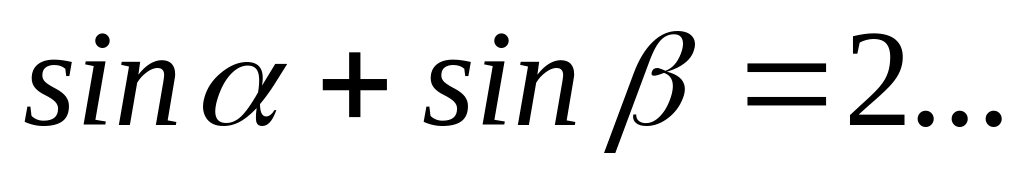 .
.Формула разности косинусов двух углов:
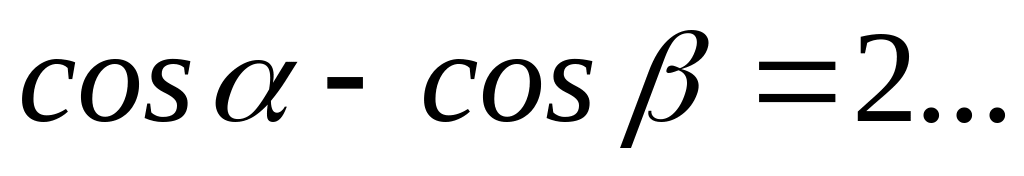 .
.Формула суммы тангенсов двух углов:
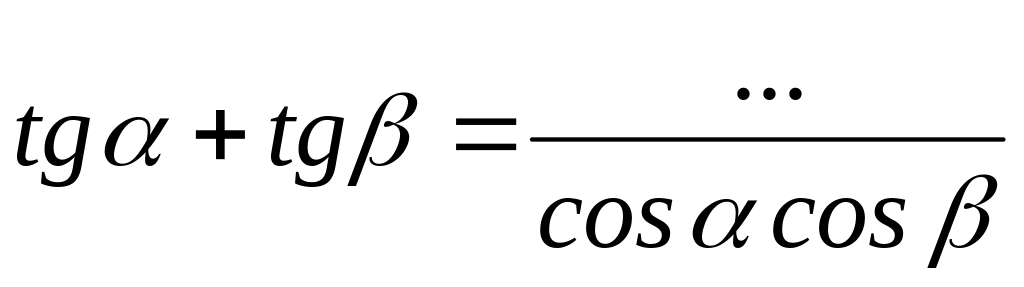 .
.Преобразуйте в произведения: а)
 ;
б)
;
б)
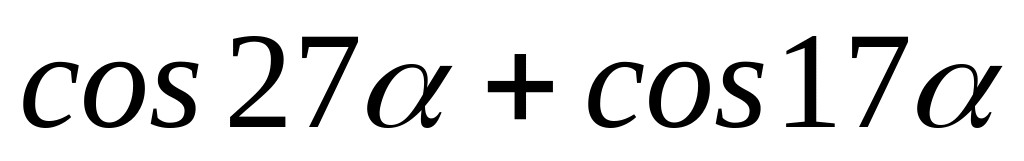 ;
в)
;
в)
 ;
;
г)
![]() .
.
Упростите: а)
 ;
б)
;
б)
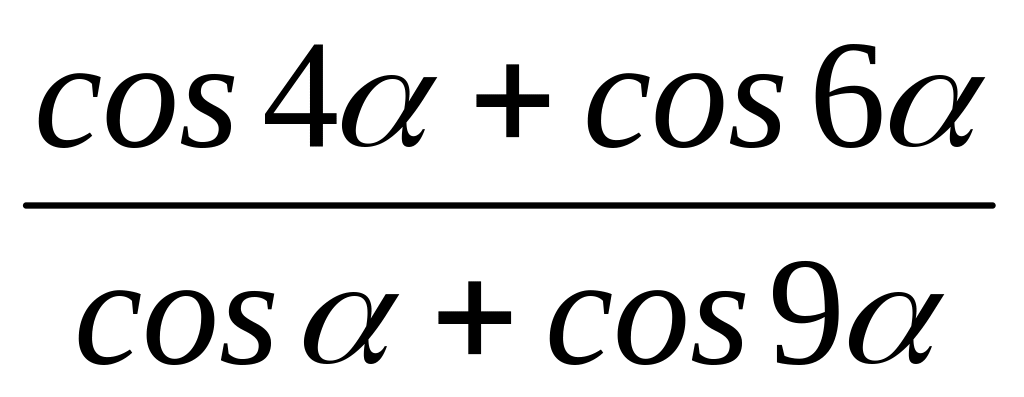 ;
в)
;
в)
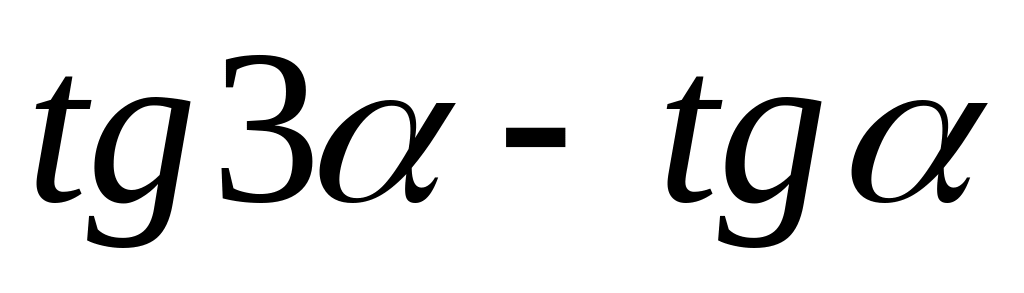 .
.Докажите тождества: а)
 ;
б)
;
б)
 .
.Докажите, что
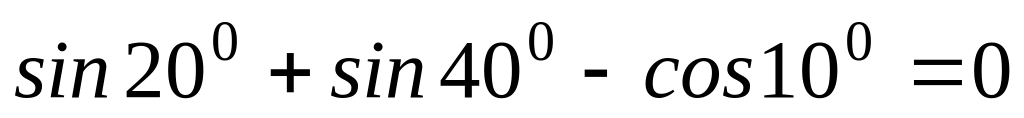 .
.
