
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
- •Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
ВАРІАНТ 1
Розв’язати систему лінійних алгебраїчних рівнянь за допомогою формул Крамера та матричним способом:

Дослідити систему рівнянь на сумісність і у випадку сумісності розв’язати її методом Гауса:
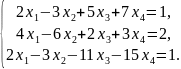
Задано вершини трикутника
 :
:
 Скласти
чи знайти:
Скласти
чи знайти:
рівняння сторін трикутника,
рівняння перпендикуляра, проведеного із
 на
на
 ,
,відстань від точки
 до
сторони
до
сторони
 ,
,рівняння медіани, проведеної з точки
 ,
,координати точки
 ,
симетричної
точці
відносно
,
симетричної
точці
відносно

Задано координати вершин піраміди



 .
Знайти:
.
Знайти:
довжину відрізка
 ,
,рівняння прямої ,
кут
 ,
,площу трикутника ,
об’єм піраміди
 ,
,довжину висоти, опущеної з вершини
 на
площину
,
на
площину
,рівняння висоти
 ,
,кут між прямою
 і
площиною
.
і
площиною
.
Звести рівняння до канонічного вигляду і визначити його геометричний образ

Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
ВАРІАНТ 2
Розв’язати систему лінійних алгебраїчних рівнянь за допомогою формул Крамера та матричним способом:

Дослідити систему рівнянь на сумісність і у випадку сумісності розв’язати її методом Гауса:

Задано вершини трикутника :
 Скласти
чи знайти:
Скласти
чи знайти:
рівняння сторін трикутника,
рівняння перпендикуляра, проведеного із на ,
відстань від точки до сторони ,
рівняння медіани, проведеної з точки ,
координати точки , симетричної точці відносно
Задано координати вершин піраміди



 .
Знайти:
.
Знайти:
довжину відрізка ,
рівняння прямої ,
кут ,
площу трикутника ,
об’єм піраміди ,
довжину висоти, опущеної з вершини на площину ,
рівняння висоти ,
кут між прямою і площиною .
Звести рівняння до канонічного вигляду і визначити його геометричний образ

Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
ВАРІАНТ 3
Розв’язати систему лінійних алгебраїчних рівнянь за допомогою формул Крамера та матричним способом:

Дослідити систему рівнянь на сумісність і у випадку сумісності розв’язати її методом Гауса:

Задано вершини трикутника :
 Скласти
чи знайти:
Скласти
чи знайти:
рівняння сторін трикутника,
рівняння перпендикуляра, проведеного із на ,
відстань від точки до сторони ,
рівняння медіани, проведеної з точки ,
координати точки , симетричної точці відносно
Задано координати вершин піраміди



 .
Знайти:
.
Знайти:
довжину відрізка ,
рівняння прямої ,
кут ,
площу трикутника ,
об’єм піраміди ,
довжину висоти, опущеної з вершини на площину ,
рівняння висоти ,
кут між прямою і площиною .
Звести рівняння до канонічного вигляду і визначити його геометричний образ

Розрахунково-графічна робота “лінійна та векторна алгебри, аналітична геометрія”
ВАРІАНТ 4
Розв’язати систему лінійних алгебраїчних рівнянь за допомогою формул Крамера та матричним способом:

Дослідити систему рівнянь на сумісність і у випадку сумісності розв’язати її методом Гауса:

Задано вершини трикутника :
 Скласти
чи знайти:
Скласти
чи знайти:
рівняння сторін трикутника,
рівняння перпендикуляра, проведеного із на ,
відстань від точки до сторони ,
рівняння медіани, проведеної з точки ,
координати точки , симетричної точці відносно
Задано координати вершин піраміди

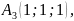
 .
Знайти:
.
Знайти:
довжину відрізка ,
рівняння прямої ,
кут ,
площу трикутника ,
об’єм піраміди ,
довжину висоти, опущеної з вершини на площину ,
рівняння висоти ,
кут між прямою і площиною .
Звести рівняння до канонічного вигляду і визначити його геометричний образ

