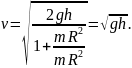ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ФИЗИКЕ
для студентов факультета экономики и управления
Лектор – Бекетов В.Г.
2014 – 2015 учебный год
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КЛАССИЧЕСКОЙ МЕХАНИКЕ
Порядок решения задачи на уравнение траектории
Задача. Даны законы поступательного
движения тела по осям
и
:
,
.
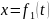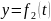Найти уравнение траектории
.
Решение.
Из первого или из второго уравнения,
где это проще, выражаем время
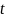и подставляем в другое уравнение. Если
время находится под знаком синуса или
косинуса, то выражаем из первого и
второго уравнени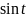й
и
и используем формулы тригонометрии.
Порядок решения прямой задачи механики
Задача. Тело массы
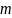движется поступательно и прямолинейно
по закону
,
м. Найти силу, импульс и кинетическую
энергию тела в заданный момент времени
(в частности, в момент изменения
направления движения).
Решение.
Сначала находим зависимость скорости тела от времени
потом зависимость ускорения от времени
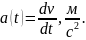
В момент изменения направления движения тело останавливается. Время остановки находим из условия
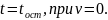
Все стальные величины найдем по второму закону Ньютона и другим формулам.
Задача. Тело с моментом инерции
вращается по закону
,
м. Найти момент силы, момент импульса и
кинетическую энергию тела в заданный
момент времени (в частности в момент
изменения направления движения).
Решение.
Сначала находим зависимость угловой скорости тела от времени
потом зависимость углового ускорения от времени
Время остановки находим из условия
Все стальные величины найдем по второму закону Ньютона и другим формулам.
Порядок решения обратной задачи механики
Задача. Тело массы
начинает двигаться (
из точки с координатой
под действием силы
.
Найдите скорость и координату тела в
некоторый момент времени
.
Решение.
Из условия задачи можно найти ускорение тела:
Для решения задачи используем формулы определения скорости и ускорения тела, из которых путем взятия определенного интеграла можно будет найти искомые зависимости и величины:
Так как начальная скорость
равна нулю,
Итак
Задача. Маховик с заданным моментом
инерции
начал вращаться
под действием момента сил
.
Найдите его угловую скорость, момент
импульса и кинетическую энергию в
некоторый момент времени
.
Решение.
Из условия задачи можно найти угловое ускорение тела:
Зависимость угловой скорости от времени находим, как и в предыдущей задаче:
Момент импульса и кинетическую энергию считаем по формулам:
Задача. Кинетическая энергия
вращающегося маховика зависит от времени
по закону:
,
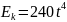Дж. Найдите его момент импульса и
вращающий момент сил через время t
= 2 c после начала движения. Момент инерции
маховика равен 20 кг·м2.
Решение.
Используем формулу кинетической энергии
вращающегося тела
и подставим в условие задачи:
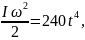
Откуда
Найдем зависимость углового ускорения от времени:
Найдем угловую скорость через время t
= 2 c после начала движения:
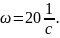
Момент импульса тела
Найдем угловое ускорение через время
t = 2 c после начала движения:
Вращающий момент сил
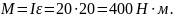
Ответ: 400 Дж∙с, 400 Н∙м.
Задача. Найдите линейное ускорение
цилиндра, если он скатывается без
скольжения с наклонной плоскости с
углом наклона
= 300 к горизонту. Масса цилиндра
m = 3 кг, его момент инерции равен
2 кг·м2, радиус R = 0,8 м.
Ускорение
принять равным 9,8 м/с2. Ответ:
2,4 м/с2.
Решение.
Исходя из условия задачи, мы знаем, что линейное ускорение цилиндра будет направлено вниз вдоль наклонной плоскости, и что при этом он будет вращаться по часовой стрелке, и при этом его угловое ускорение также будет направлено по часовой стрелке. Сделаем рисунок.
или
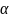
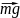
На цилиндр действуют два
тела: Земля и наклонная плоскость.
Активной
силой является сила, с которой Земля
действует на цилиндр. Эта сила есть сила
тяжести
.
Она направлена вертикально вниз. Эта
сила тяжести имеет две проекции (две
составляющие):
,
перпендикулярную наклонной
плоскости, и
,
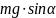направленную вниз вдоль наклонной
плоскости. Сила тяжести
оказывает двойное действие на цилиндр:
прижимает его к наклонной плоскости
перпендикулярно ей с силой
и стаскивает его вдоль наклонной
плоскости с силой
.
Ответ – реакцию на эти две составляющие дает наклонная плоскость. В ответ на прижимающую силу наклонная плоскость действует с силой нормальной реакции , направленной противоположно прижимающей силе. Прижатый к наклонной плоскости цилиндр по условию не скользит вдоль наклонной плоскости. Это потому, что в ответ на стаскивающую силу наклонная плоскость действует на цилиндр с силой трения покоя , направленной вдоль наклонной плоскости в противоположном направлении.
Применим уравнение второго закона Ньютона в векторной форме:
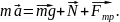
Исходя из условия задачи, мы знаем, что линейное ускорение цилиндра будет направлено вдоль наклонной плоскости, перпендикулярно наклонной плоскости ускорения нет. Поэтом запишем уравнение второго закона Ньютона в проекции на ось, совпадающую с направлением ускорения, то есть вдоль наклонной плоскости вниз. Это первое уравнение справа от рисунка.
Этого уравнения недостаточно для
решения задачи, поскольку в нем две
неизвестных величины:
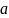и
.
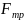Это естественно, потому что цилиндр еще
и вращается. Поэтому запишем уравнение
второго закона Ньютона для вращательного
движения в проекции на направление
вращения. Это второе уравнение справа
от рисунка.
Появилось новая неизвестная
величина – угловое ускорение
.
Формула связи между угловым и линейным
ускорением (третье уравнение справа от
рисунка) замкнет систему уравнений.
После преобразований, сделанных справа от рисунка, мы получили решение задачи, то есть нашли формулы для расчета линейного ускорения цилиндра.
Если цилиндр полый, применим формулу
для момента инерции полого цилиндра
Получим для расчета ускорения
Задача. Катушка висит на нити, которая намотана на эту катушку. Нить расположена строго вертикально. Катушка расположена строго горизонтально. Масса катушки 25 г, ее момент инерции равен 3,6∙10-6 кг∙м2. Радиус катушки равен 1,5 см. Катушка, вращаясь, движется с ускорением вниз. При этом нить не скользит по катушке. Найдите ускорение катушки. Ускорение свободного падения примите равным 9,8 м/с2. Ответ: 6,0 м/с2.
Решение.
Исходя из условия задачи, мы знаем, что линейное ускорение цилиндра будет направлено вертикально вниз, и что при этом он будет вращаться по часовой стрелке, и при этом его угловое ускорение также будет направлено по часовой стрелке. Сделаем рисунок.
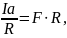
или
На цилиндр действуют два тела: Земля и нить. Активной силой является сила, с которой Земля действует на цилиндр. Эта сила есть сила тяжести . Она направлена вертикально вниз. Сила тяжести тянет цилиндр вертикально вниз. Цилиндр при этом растягивает нить.
В ответ на свое растяжение нить действует на цилиндр с силой реакции , направленной вдоль нити вертикально вверх.
Применим уравнение второго закона Ньютона в векторной форме:
Исходя из условия задачи, мы знаем, что линейное ускорение цилиндра будет направлено вертикально вниз. Поэтому запишем уравнение второго закона Ньютона в проекции на ось, совпадающую с направлением ускорения, то есть вертикально вниз. Это первое уравнение справа от рисунка.
Этого уравнения недостаточно для
решения задачи, поскольку в нем две
неизвестных величины:
и
.
Это естественно, потому что цилиндр еще
и вращается. Поэтому запишем уравнение
второго закона Ньютона для вращательного
движения в проекции на направление
вращения. Это второе уравнение справа
от рисунка.
Появилось новая неизвестная величина – угловое ускорение . Формула связи между угловым и линейным ускорением (третье уравнение справа от рисунка) замкнет систему уравнений.
После преобразований, сделанных справа от рисунка, мы получили решение задачи, то есть нашли формулы для расчета линейного ускорения цилиндра.
Посчитаем величину линейного ускорения цилиндра:
Если цилиндр сплошной, применим формулу
для расчета момента инерции сплошного
цилиндра:
Получим для расчета ускорения
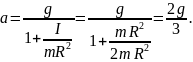
Задача. Найти скорость образовавшегося тела при абсолютно неупругом соударении двух шаров, если шары движутся или в одну сторону или навстречу друг другу.
Решение.
Предполагается, что при ударе шары
слипнутся, образовав одно тело с массой
.
При этом суммарный импульс тел
сохранится в соответствии с уравнением
Если шары до удара двигались в одном направлении, причем скорость первого догоняющего шара больше скорости второго шара, то проекция этого векторного уравнения на направление движения будет выглядеть так:
откуда
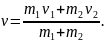
Если шары до удара двигались навстречу друг другу, то проекция этого векторного уравнения на направление движения первого шара будет выглядеть так:
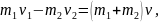
откуда
Если проекция скорости окажется отрицательной, то образовавшееся тело будет двигаться в сторону, противоположную движению первого шара до удара.
Задача. Пуля, масса которой 10 г и скорость 500 м/с, попадает в дверь ширины l = 120 см и застревает в ней на расстоянии a = 80 см от оси. Масса двери равна 60 кг. Найдите угловую скорость двери после попадания в нее пули (скорость пули перпендикулярна плоскости двери). Ответ: 0,14 1/с.
Решение.
Сделаем рисунок.
Летящая пуля обладает
импульсом
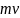и моментом импульса
относительно оси, на которой закреплена
дверь. Плечо импульса пули равно
.
Пуля, попав в дверь и застряв в ней, толкнет дверь. Но дверь закреплена на своей оси, и сила реакции, возникшая со стороны этой оси, подействует на дверь и поменяет суммарный импульс пули и двери. Однако у этой силы реакции нет плеча, поскольку она проходит через ось. Следовательно, эта сила не сможет создать вращающий момент.
Только момент внешних сил
может изменить суммарный момент импульса
пули и двери. И поскольку момент внешних
сил равен нулю сохраняется суммарный
момент импульса пули и двери. До удара
момент импульса был только у пули, а
после удара и у пули, и у двери. Причем,
поскольку пуля застряла в двери, вращаться
они будут с одной и той же угловой
скоростью
.
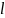
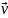
Запишем уравнение сохранения момента импульса:
где
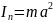– момент инерции пули (как материальной
точки на расстоянии
от оси),
– момент инерции двери.
Из этой формулы выразим угловую скорость:
Задача.
Найти новую угловую скорость вращения
легкого жесткого стержня при изменении
положения грузиков с массами
и
,
если задана первоначальная скорость
вращения. Или найти, во сколько раз
изменится угловая скорость вращения.
Решение.
Предполагается, что изменение положения грузов произошло без воздействия внешней силы, грузы взаимодействуют только со стержнем. В этом случае сохраняется момент импульса двух грузов (момент инерции и момент импульса стержня равны нулю, так как по условию он не имеет массы):
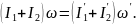
Моменты инерции грузов
считаем по формуле для материальных
точек на расстоянии
от оси (
:
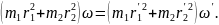
Теперь можно найти новую угловую скорость вращения стержня по формуле
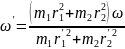
или отношение скоростей по формуле
Задача.
По горизонтальной поверхности катится
без скольжения цилиндр со скоростью
0,32 м/с. Масса цилиндра 126 г, его радиус
2,5 см, а момент инерции относительно
своей оси равен 6,5∙10-5
кг∙м2.
Найдите кинетическую энергию цилиндра.
Ответ:
.
Решение.
Кинетическая энергия
цилиндра складывается из кинетической
энергии его поступательного движения
со скоростью
и кинетической энергии его вращательного
движения с угловой скоростью
.
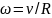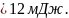
Если катящийся цилиндр сплошной, то его кинетическая энергия равна
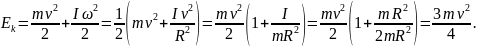
Если катящийся цилиндр полый, то его кинетическая энергия равна
Задача.
По наклонной плоскости с высоты 25 см
скатывается без скольжения цилиндр
массы 254 г. Радиус цилиндра 2,50 см, а момент
инерции относительно своей оси равен
1,3∙10-4
кг∙м2.
Начальная скорость цилиндра равна 0.
Найдите скорость цилиндра в конце
наклонной плоскости. Потерями энергии,
связанными с трением, можно пренебречь.
Ускорение свободного падения примите
равным 9,8 м/с2. Ответ:
.
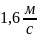Решение.
С уменьшением высоты положения цилиндра его потенциальная энергия в поле силы тяжести полностью превращается в кинетическую энергию, поскольку потерями энергии, связанными с трением, можно пренебречь.
Кинетическая энергия цилиндра складывается из кинетической энергии его поступательного движения со скоростью и кинетической энергии его вращательного движения с угловой скоростью (см. предыдущую задачу).
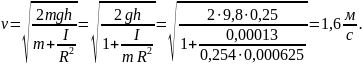
Если катящийся цилиндр сплошной, то его скорость в конце наклонной плоскости равна
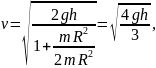
Если катящийся цилиндр полый, то его скорость в конце наклонной плоскости равна
