3.3 Розрахунок підшипників кочення

Розраховуємо підшипники кочення для ведучого вала. Попередньо для опори вала приймаємо роликові підшипники конічні [3.т.П.9 с.320] 27308А. Зміщення точки прикладення радикальної реакції відносно торця підшипника по формулі:

a₁ =

Відстань між точками прикладення активних і реактивних сил.

l₁ =70 мм F_r1 =1017,1 Н

l₂ =97 мм F_a1 =2794,4 Н

F_t1 =517 Н d₁ =72,5 мм

Виконуємо розрахункову схему вала-червяка.

Визначаємо опорні реакції вала від навантаження в зачіпці.

В горизонтальній площині в силу симетричності маємо:

R_zA =R_zB =

У вертикальній площині:

∑T_z =0

F_r1l₁-

Звідки

R_yB =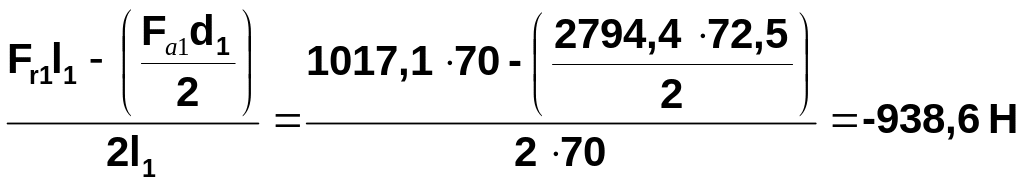

∑T_z =0

R_yA2l₁-F_r1l₁- /2l₁ =

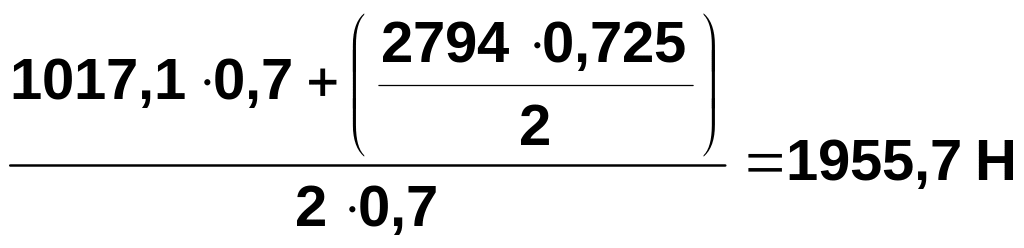
Перевірка

∑R_yA-F_r1+R_yB =1955,7-1017,1+(-938,6)=0

Сумарні радіальні реакції підшипників:

Для опори А

R_A =

Для опори В

R_B = 973,7 Н

Внаслідок виникаючої неспіввісності з’єднувальних валів редуктора та електродвигуна муфта навантажує вал допоміжною консольною силою F_к ,котра у випадку застосування муфти пружинно – втулочно - пальцевій знаходяться по виразу:

F_к =23

Визначаємо опорні реакції вала від консольного навантаження викликане муфтою:

∑T_A =0; R_BM·2l₁-F_kl₂ =0

R_BM =

∑T =0; R_AM·2l₁-F_k(2l₁-l₂)=0

R_AM =F_k

Визначаємо сумарні опорні реакції ведучого вала від навантаження в зачіпці та муфти. Розглянемо гірший випадок:

F_rA =R_A+R_AM =1972,8+284,4=2257,2 Н

F_rB =R_B+R_BM =973,7+116,4=1090,1 Н

Визначаємо базову довго тривалість прийнятого роликопідшипника 27308А.

Вихідні дані:

F_rA =2257,2 Н n₂ =1455 Y =0,72

F_rB =1090,1 Н C_r =69300

F_a1 =2794,4 Н e =0,83

Осьові складові:

F_ =0,83еF_rA =0,830,832257,2 =1555 H

F_ = 0,83еF_rB =0,830,831090,1 =751 H

Сума усіх осьових сил, діючих на опору А:

F_a1+F_-F_ =2794,4+751-15550, тому

F_aF_a1F_ =2794,4+751 =3545,4 H

F_a =F_ =751 H

Розрахунок ведемо по найбільш навантаженому підшипнику А. Та як

е =0,83

то X=0,4; Y=0,72

Еквівалентне динамічне навантаження

P_rA =(X·F_rA+Y·F_aA)K_б =(0,4·2257,2+0,72·3545,4)·1,3 =3789,3 Н

Базова довго тривалість підшипника 27308А.

L_h =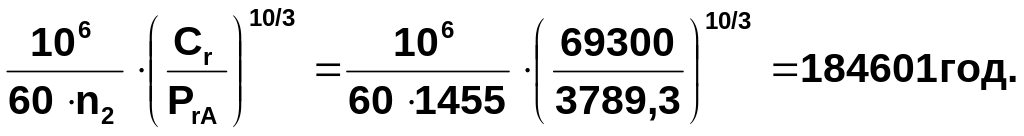

Відомий вал.

Для опор валу приймаємо роликопідшипники конічні середньої серії 7310.

Зсув точки прикладення радіальної реакції відносно торця підшипника:

а₂ =

Відстань між точками прикладення активних сил:

l₃ =53 мм F_t =5910 Н

l₄ =85 мм F_r2 =1017,1 Н

F_r =2151 Н F_a2 =517 Н

F_t2 =2794,4 Н d₂ =205,5 мм

У горизонтальній площині:

∑T_y =0; F_r·(l₄+2l₃)-R_zD2l₃-F_t2l₃ =0

R_zD =

∑T_y =0; F_rl₄+F_t2l₃-R_zC2l₃ =0

звідси:

R_zC =

Перевірка:

∑z =R_zC-F_t2-R_zD+F_r =3122-2794-2479+2151 =0

У вертикальній площині:

∑T_z =0; F_t(l₄+2l₃)-R_yD2l₃-F_r2l₃+F_a2d₂/2 =0

Звідси

R_yD=

= = =10642 Н

∑T_z' =0; F_tl₄+F_r2l₃+F_a2d₂/2-R_yC2l₃ =0

звідси

R_yC = = 5749 Н

Перевірка:

∑y =-F_t+R_yD+F_r2-F_yC =-5910+10642+1017-5749 =0

Сумарні реакції підшипників:

Для опори С

R_C =

Для опори D

R_D =

Знаходимо довго тривалість роликопідшипника 7310

Вихідні дані:

F_rC =R_C =6542 Н C_r =100000

F_rD =R_D =10927 Н e =0,310

F_a2 =517 Н Y =1,34

n₃ =80,83

Осьові складаючи по формулі:

F_C =0,83eF_rC =0,830,3106542 =1683 H

F_D =0,83eF_rD =0,830,31010927 =2812 H

Оскільки сума усіх осьових сил діючих на опору С додаткова

F_a2 +F_D -F_C =517+2812-1683 0

тоді розрахункова осьова сила до опори С

F_a2 +F_D -F_C =517+2812=3329 Н

Для опори D

F_CF_a F_D =1683-517-2812 0

Тому:

F_aD =F_D =2812 H

Із розрахунків одразу не бачимо, який з підшипників найбільш навантажений. Тому знаходимо еквівалентне динамічне навантаження на обидва підшипника.

Спочатку розглянемо підшипник С:

Так як е =0,310

Тоді X=0,4; Y =1,34. Еквівалентне динамічне навантаження

P_rC =(X·F_rC-Y·F_aC)K_б =(0,4·6542-1,34·3329)·1,3 =-2397,3 Н

Розглянемо підшипник D:

Так як 0,26<е =0,310

Тоді Y=0; X =1.

Еквівалентне динамічне навантаження

P_rD =F_rD·K_б =10927·1,3 =14205 Н

Знаходимо базову довго тривалість більш навантаженого підшипника D:

L_h =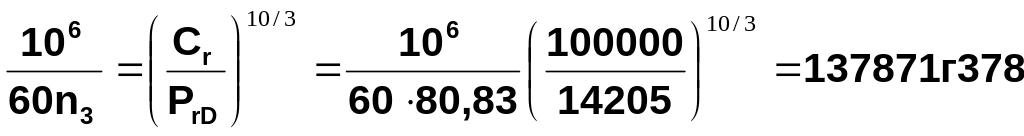

Даний підшипник підходить для встановлення на тихохідному влі.