
- •Э.Н. Сабуров
- •Основные положения теории конвективного теплообмена в однофазной среде
- •1.1 Основные понятия и определения
- •Температура потока, соответствующая среднемассовой энтальпии в сечении канала, определенная по формуле
- •1.2 Дифференциальные уравнения конвективного теплообмена
- •Уравнения неразрывности
- •1.2.2 Уравнения движения
- •1.2.3 Уравнение энергии
- •При стационарном поле температур
- •1.3. Дифференциальные уравнения конвективного теплообмена в безразмерном виде
- •1.4. Критерии, определяющие числа подобия и уравнения подобия конвективного теплообмена
- •1.5. Физические свойства теплоносителей и влияние их изменения от температуры на интенсивность конвективного теплообмена
- •1.6 Основные понятия и определения теории турбулентного движения
- •1.7 Тепловой пограничный слой
- •1.7.1 Основные понятия и определения
- •1.7.2 Ламинарный тепловой пограничный слой
- •Последний член равенства (1.279) по условию сплошности равен нулю. Тогда уравнение (1.274) представим так
1.3. Дифференциальные уравнения конвективного теплообмена в безразмерном виде
Для того чтобы выяснить условия подобия процессов конвективного теплообмена приведем дифференциальные уравнения конвективного теплообмена к безразмерному виду.
В качестве примера рассмотрим стационарный конвективный теплообмен вязкой жидкости, движущейся с умеренной скоростью и имеющей неизменные физические характеристики (ρ = const, μ = const, λ = const). Внутренние источники теплоты в движущейся жидкости отсутствуют. Температура и скорость невозмущенного (набегающего) потока соответственно равны Т0 и V0. Поверхность теплообмена имеет постоянную равномерно распределенную температуру Tc. Ее характерный линейный размер l0.
Для рассматриваемой задачи дифференциальные уравнения конвективного теплообмена и уравнение теплоотдачи имеют вид
(1.144)![]()
![]() .
(1.145)
.
(1.145)
Граничные условия задачи:
в области невозмущенного потока
![]() .
(1.146)
.
(1.146)
на поверхности теплообмена
![]() .
(1.147)
.
(1.147)
Для приведения
уравнений к безразмерному виду используем
метод масштабных преобразований. В
качестве масштаба длин выберем характерный
для исследуемого явления линейный
размер l0,
скоростей – характерную скорость V0,
массовых сил, отнесенных к единице массы
– ускорение силы тяжести, температуры
– избыточную температуру невозмущенного
(набегающего) потока
![]() Выразим величины, входящие в рассматриваемые
уравнения, в принятых масштабах. Они
примут безразмерный вид. Обозначим
безразмерные величины теми же буквами,
что и размерные, но с черточкой сверху.
Тогда можем записать
Выразим величины, входящие в рассматриваемые
уравнения, в принятых масштабах. Они
примут безразмерный вид. Обозначим
безразмерные величины теми же буквами,
что и размерные, но с черточкой сверху.
Тогда можем записать
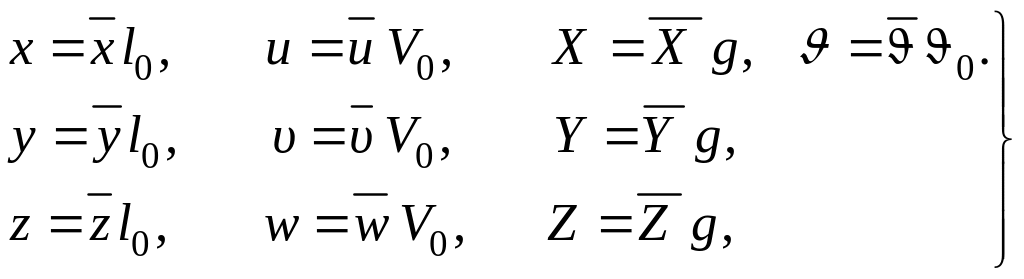 (1.148)
(1.148)
Уравнения Навье-Стокса после подстановки в них полученных соотношений и элементарных преобразований принимают вид
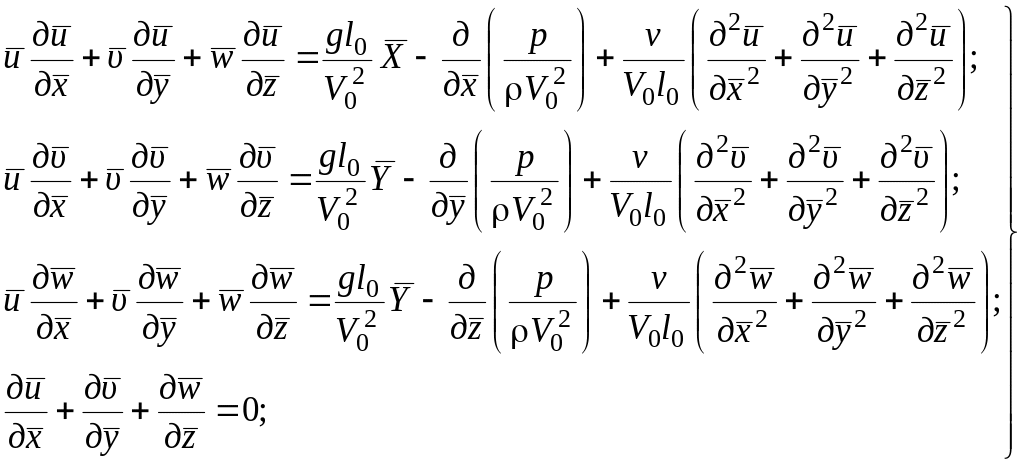 (1.149)
(1.149)
Используя общепринятые обозначения для безразмерных комплексов, полученные безразмерные уравнения (1.149) можно записать в виде
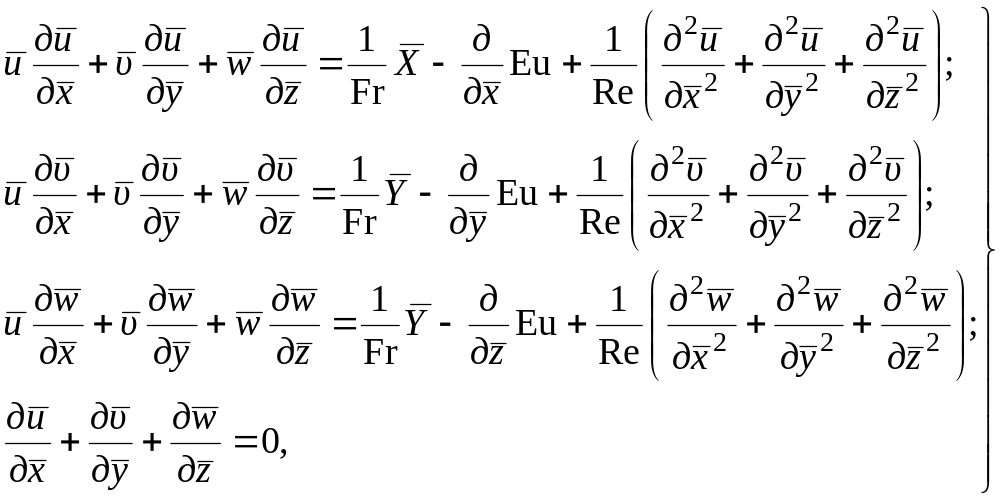 (1.150)
(1.150)
где
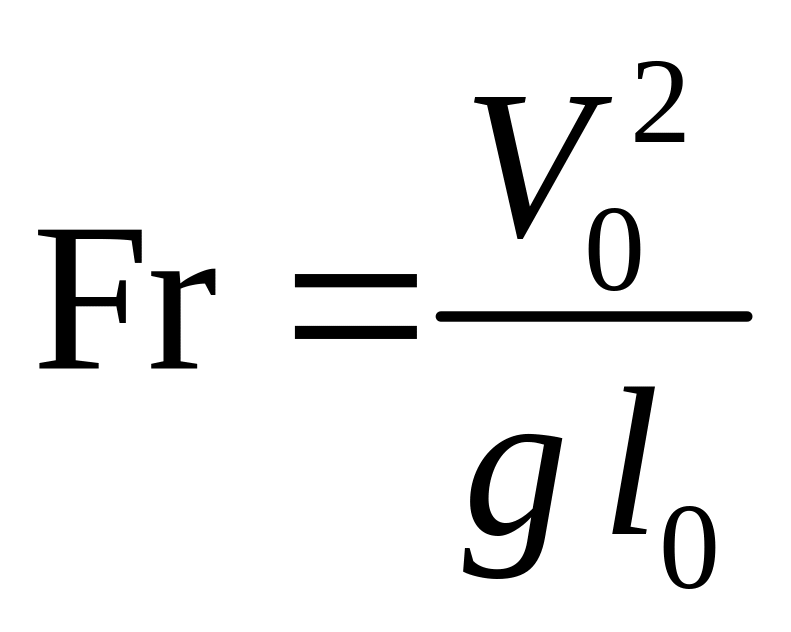 –
число Фруда (Froud
number);
–
число Фруда (Froud
number);
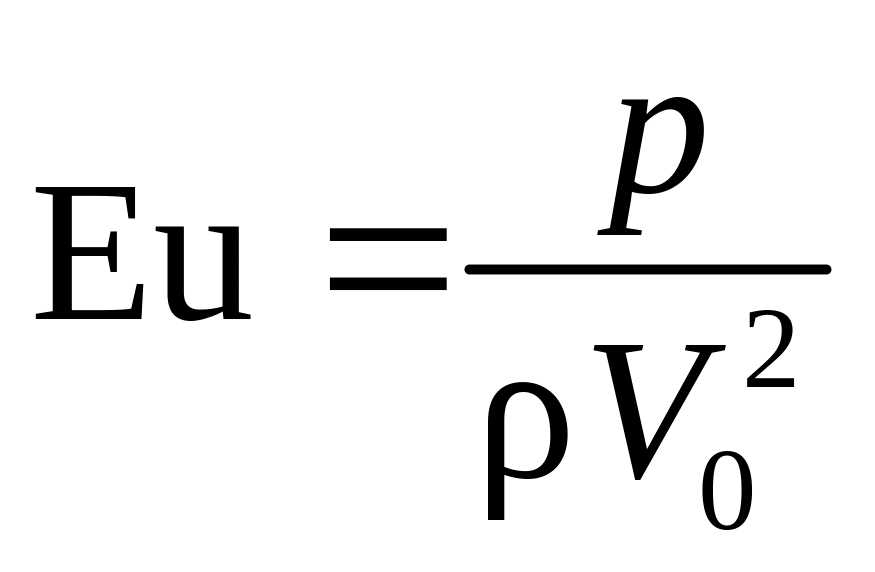 –
число Эйлера (Euler
number);
–
число Эйлера (Euler
number);
![]() – число Рейнольдса
(Reynolds
number).
– число Рейнольдса
(Reynolds
number).
Заметим, что
аналогичным образом можно привести к
безразмерному виду и уравнения (1.70),
(1.71). Так, если ось x
считать совпадающей по направлению с
![]() ,
то для стационарных условий уравнение
(1.67) можно записать следующим образом:
,
то для стационарных условий уравнение
(1.67) можно записать следующим образом:
![]() (1.151)
(1.151)
где
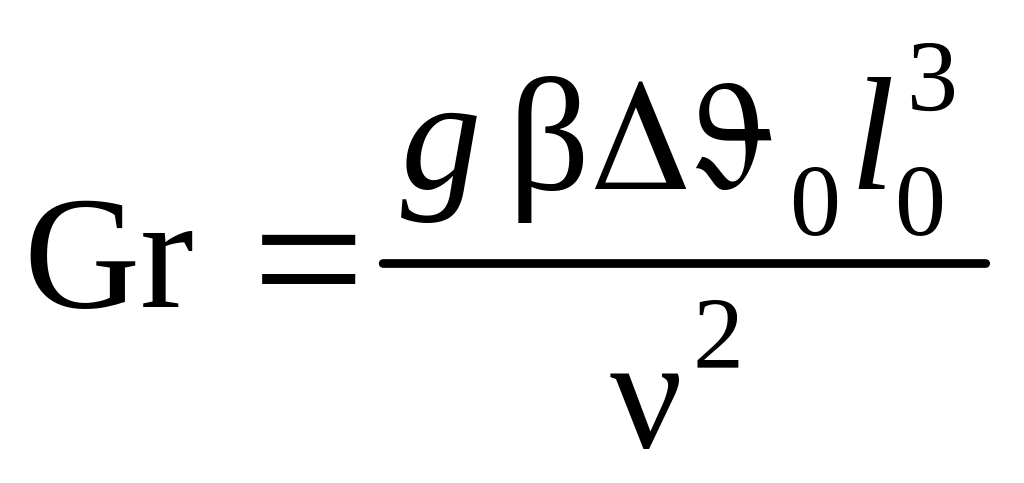 – число Грасгофа
(Grashof
number);
– число Грасгофа
(Grashof
number);
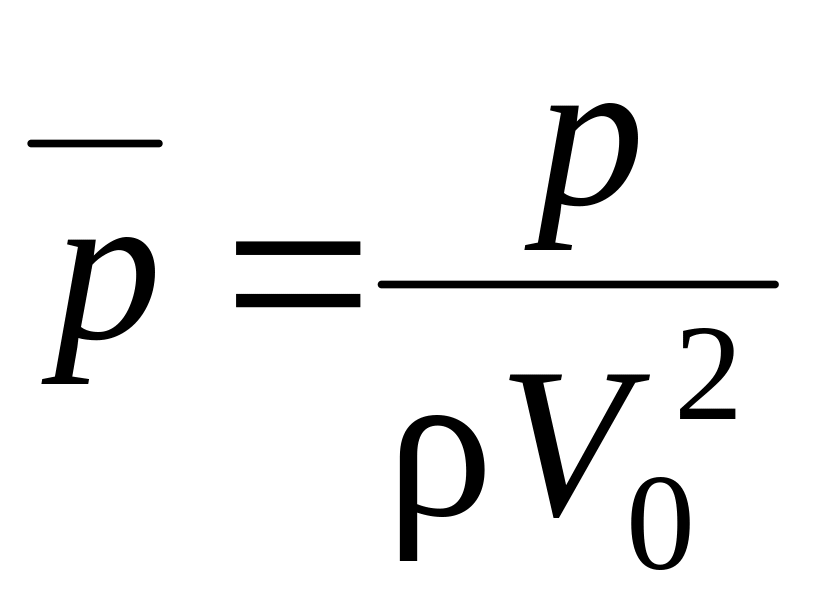 –
безразмерное
давление.
–
безразмерное
давление.
Уравнение теплоотдачи после подстановки в него размерных величин, выраженных через безразмерные и принятые масштабы, принимает вид
![]() .
(1.152)
.
(1.152)
Произведя перегруппировку членов уравнения (1.152), представляем его так
![]() .
(1.153)
.
(1.153)
Безразмерный комплекс, стоящий в левой части уравнения (1.153)
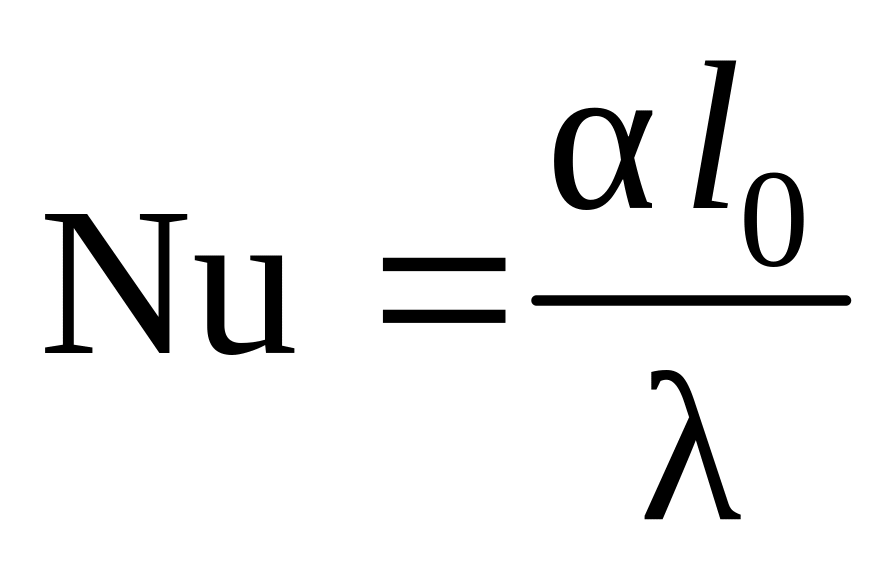 – число Нуссельта
(Nusselt
number).
– число Нуссельта
(Nusselt
number).
Поэтому уравнение теплоотдачи окончательно в безразмерном виде можем записать следующим образом:
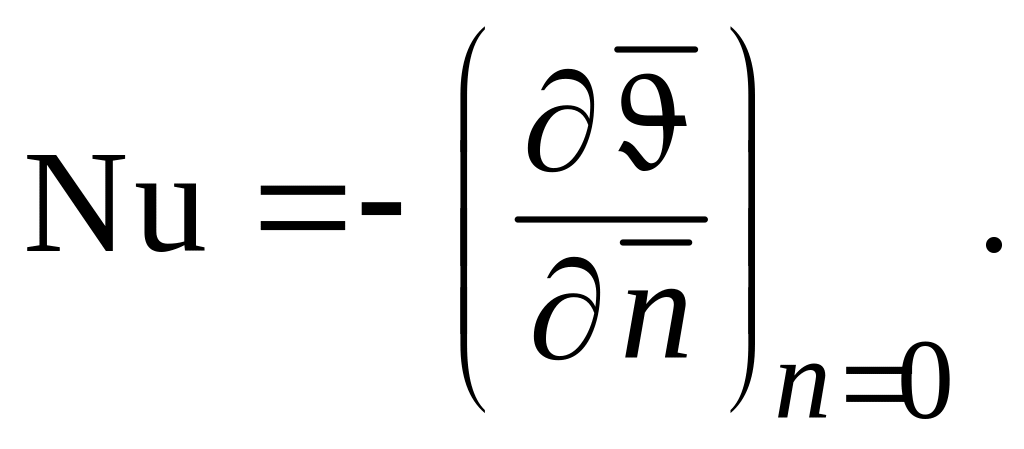 (1.154)
(1.154)
Аналогично к безразмерному виду приведем уравнение энергии, которое в результате примет вид
 (1.155)
(1.155)
или
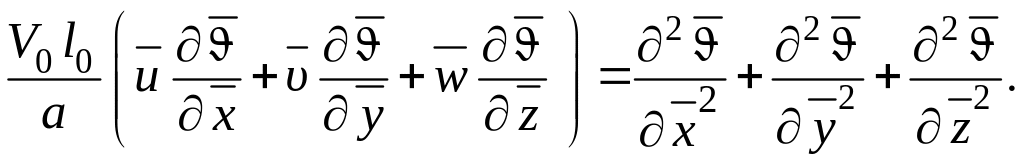 (1.156)
(1.156)
Безразмерный комплекс
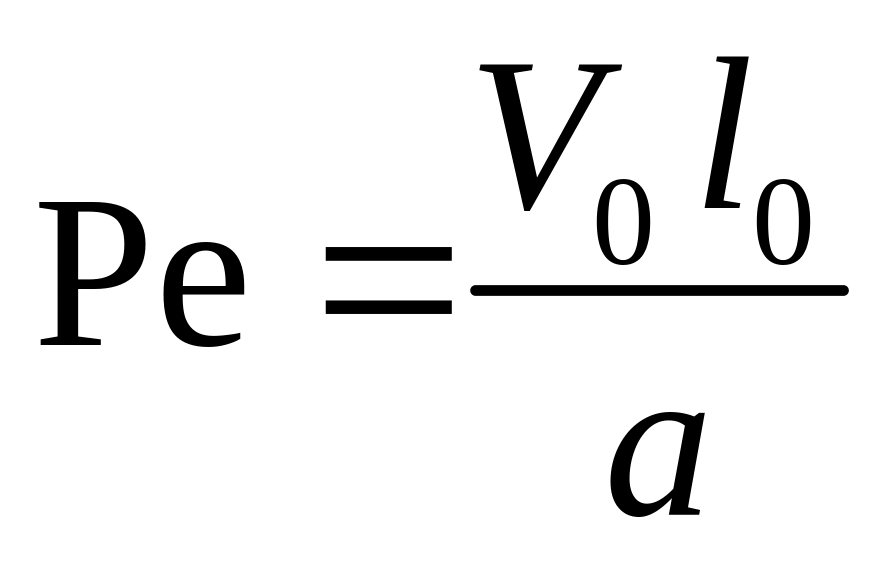 –
число Пекле (Peclet
number).
–
число Пекле (Peclet
number).
Окончательно уравнение энергии в безразмерном виде для рассматриваемого случая имеет вид
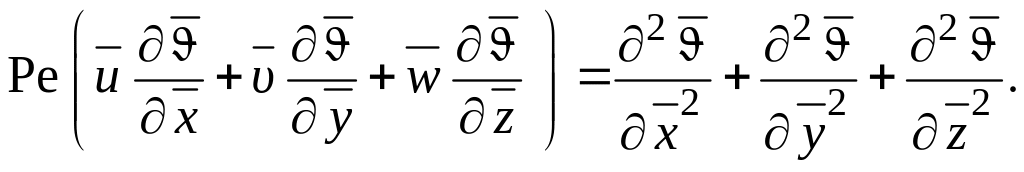 (1.157)
(1.157)
Таким образом, система дифференциальных уравнений конвективного теплообмена и теплоотдачи в безразмерном виде может быть представлена так
(1.158)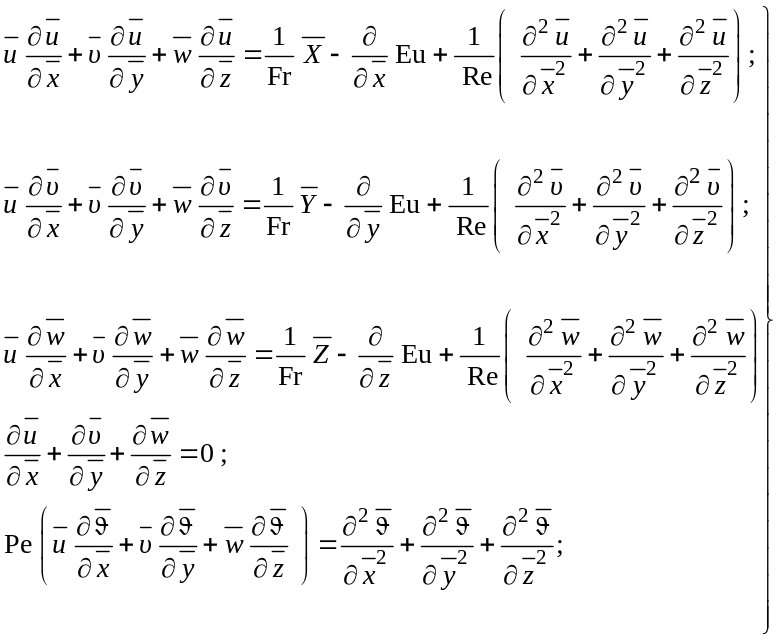
 (1.159)
(1.159)
В векторном виде эта система уравнений запишется следующим образом:
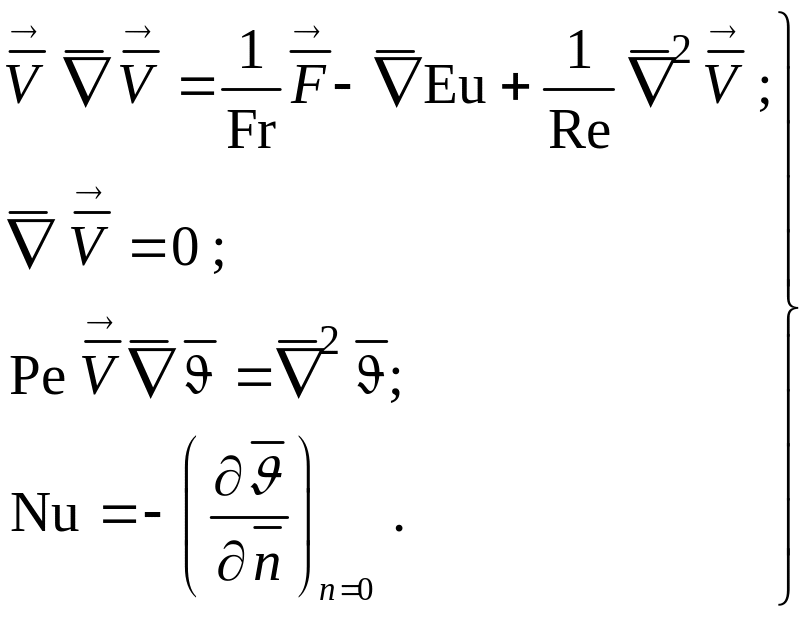 (1.160)
(1.160)
Как и раньше черточка над величиной показывает, что она безразмерная, стрелка показывает, что она векторная.
Граничные условия задачи также должны быть приведены к безразмерному виду. В рассматриваемом случае в безразмерном виде граничные условия имеют следующий вид:
в области невозмущенного потока
![]() (1.161)
(1.161)
на поверхности теплообмена
![]() (1.162)
(1.162)
Анализ полученной системы дифференциальных уравнений конвективного теплообмена и теплоотдачи в безразмерном виде показывает, что явления или процессы конвективного теплообмена будут подобны, если они описываются одной и той же системой дифференциальных уравнений, имеют подобные условия однозначности и численно одинаковые критерии подобия.
Fr = idem;
Re = idem;
Pe = idem.
К безразмерному виду могут быть приведены и уравнения, описывающие стационарное течение вязкой жидкости, находящейся под воздействием одновременно гравитационных и центростремительных массовых сил, в системе координат, вращающейся с постоянной угловой скоростью ω.
Используем в качестве масштабных характерные величины системы: l0 – линейный размер; V0 – скорость; ω0 – угловую скорость.
Тогда
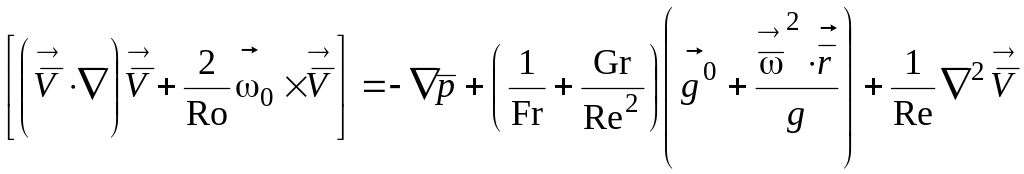 ;
(1.163)
;
(1.163)
![]() , (1.164)
, (1.164)
где
![]() - число Росби;
- число Росби;
![]() - число Фруда;
- число Фруда;
![]() - число Грасгофа;
- число Грасгофа;
![]() - орт угловой скорости вращения;
- орт угловой скорости вращения;
![]() -
орт ускорения силы тяжести;
-
орт ускорения силы тяжести;
![]() - центростремительное ускорение.
- центростремительное ускорение.
Для течения жидкости
в трубах характерным линейным размером
l0
является диаметр трубы
![]() ,
характерной скоростью
,
характерной скоростью
![]() - средняя скорость течения жидкости в
трубе
- средняя скорость течения жидкости в
трубе
![]() ,
характерной угловой скоростью – угловая
скорость вращения трубы
,
характерной угловой скоростью – угловая
скорость вращения трубы
![]() .
.
Второй член в левой части уравнения (1.147) учитывает влияние кориолисова ускорения. Его величина по сравнению с инерционными членами оценивается по значению числа Росби.
Безразмерный комплекс Ro – число Росби (Rosby number):
(1.165)
По физическому
смыслу число Росби*,
являющееся числом подобия, можно
определить как отношение конвективного
ускорения к ускорению Кориолиса**,
которое равно
![]() .
.
Влияние сил
Кориолиса на вынужденное течение
жидкости во вращающихся каналах будет
существенным при его сравнительно малой
интенсивности и значении числа Росби
![]() .
.
Член
![]() в правой части уравнения (1.163) характеризует
вклад центростремительного ускорения.
в правой части уравнения (1.163) характеризует
вклад центростремительного ускорения.
При величине центростремительного ускорения, намного превышающей значение ускорения силы тяжести, уравнение (1.163) целесообразно записать в виде
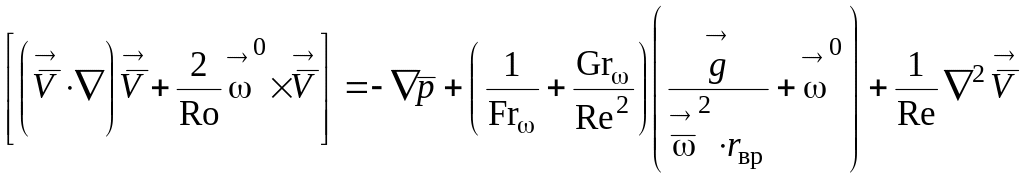 (1.166)
(1.166)
где
![]() - «вращательное» число Грасгофа,
- «вращательное» число Грасгофа,
![]() ; (1.167)
; (1.167)
![]() - «вращательное»
число Фруда,
- «вращательное»
число Фруда,
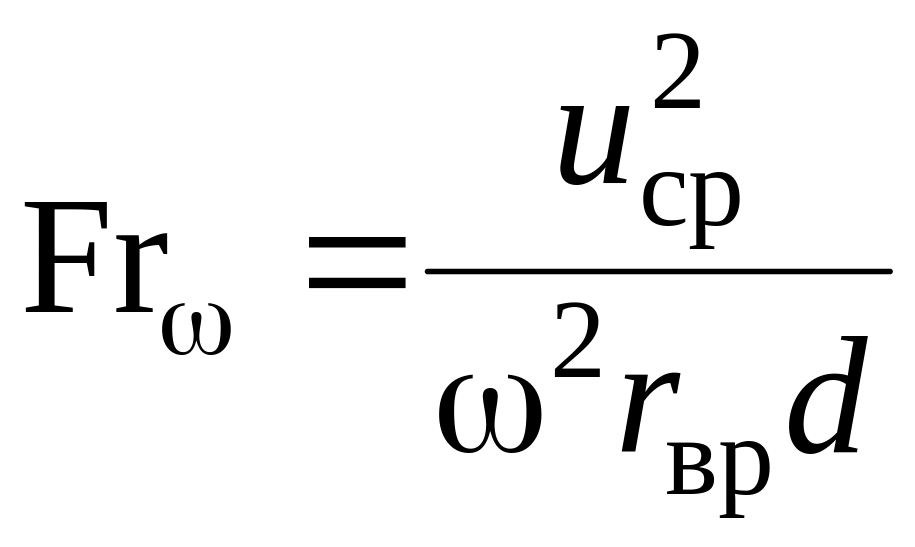 . (1.168)
. (1.168)
Из уравнений (1.163), (1.167) видно, что характер течения жидкости во вращающейся системе в общем случае определяется критериями Fr, Re, Gr, Ro или , Re, , Ro.
