Температура потока, соответствующая среднемассовой энтальпии в сечении канала, определенная по формуле

, (1.9)

называется среднемассовой температурой (bulk temperature).

Если теплоемкость с_p не зависит от температуры

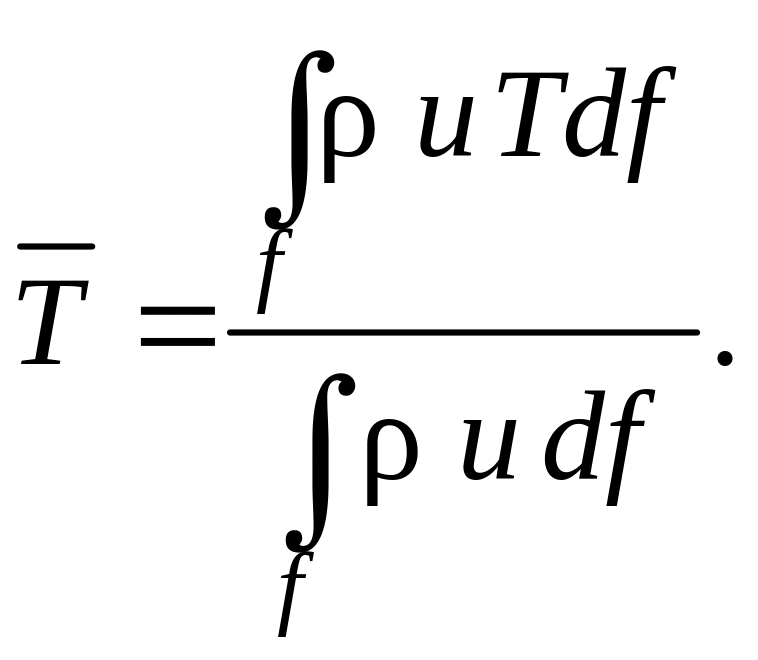(1.10)

Если ρ = const и c_p = const, то

(1.11)

В задачах конвективного теплообмена различают местный и средний температурные напоры.

Средний интегральный температурный напор

(1.12)

или

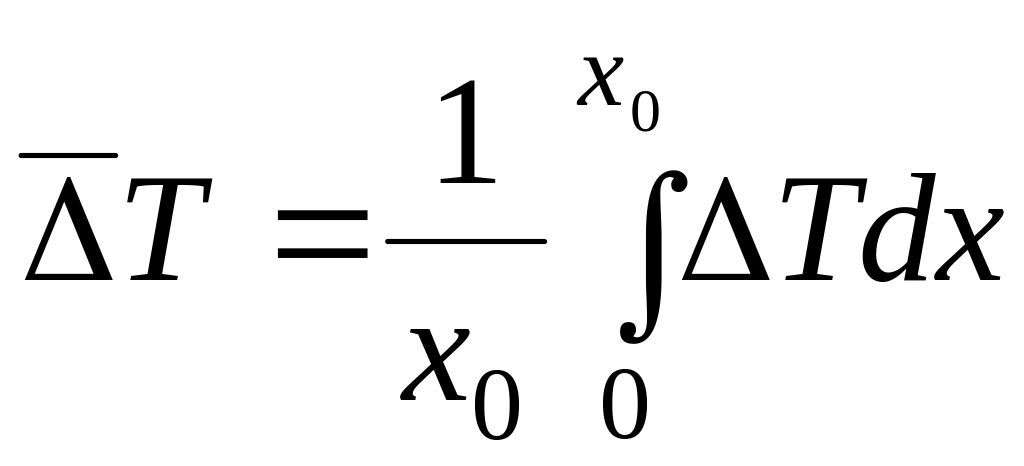, (1.13)

где ∆Т(F) или ∆Т(x) – местные температурные напоры.

Средний логарифмический температурный напор

, (1.14)

где ∆Т₁, ∆Т₂ – значения местного температурного напора в начале и в конце (по ходу потока теплоносителя) теплообменной системы.

Средний арифметический температурный напор

. (1.15)

Для элементарной поверхности закон Ньютона-Рихмана

d Q_c = α ∆ Td F, (1.16)

Величина

(1.17)

носит название местной (локальной) плотности теплового потока или тепловой нагрузки поверхности теплоотдачи.

Кроме местной плотности теплового расчета в расчетах используют и среднюю по поверхности плотность теплового потока.

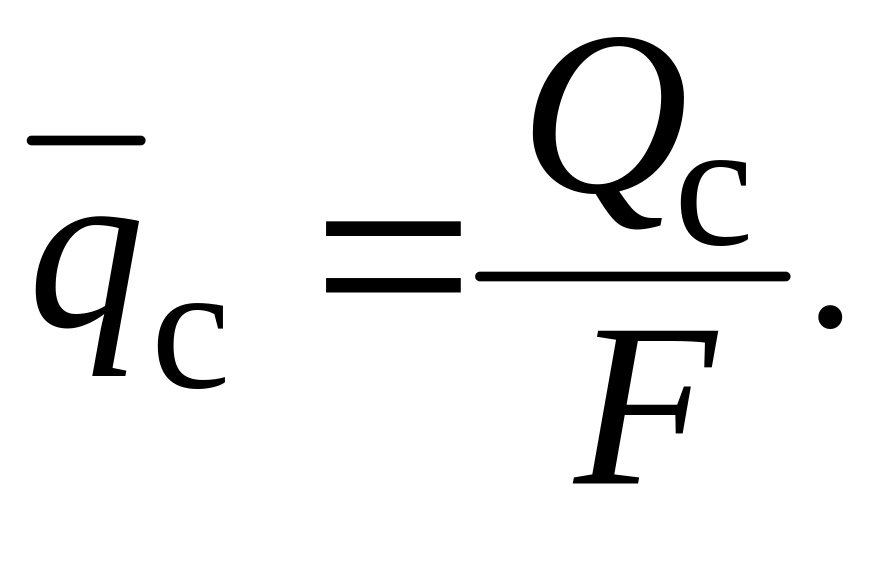(1.19)

Местный коэффициент теплоотдачи (local heat transfer coefficient) – коэффициент теплоотдачи в данной точке поверхности теплообмена, равный местной плотности теплового потока в этой точке, отнесенной к местному температурному напору

(1.20)

Размерность местного коэффициента теплоотдачи .

Средний коэффициент теплоотдачи (average heat-transfer coefficient) – коэффициент теплоотдачи равный тепловому потоку через поверхность теплообмена, деленному на средний температурный напор и площадь поверхности теплообмена

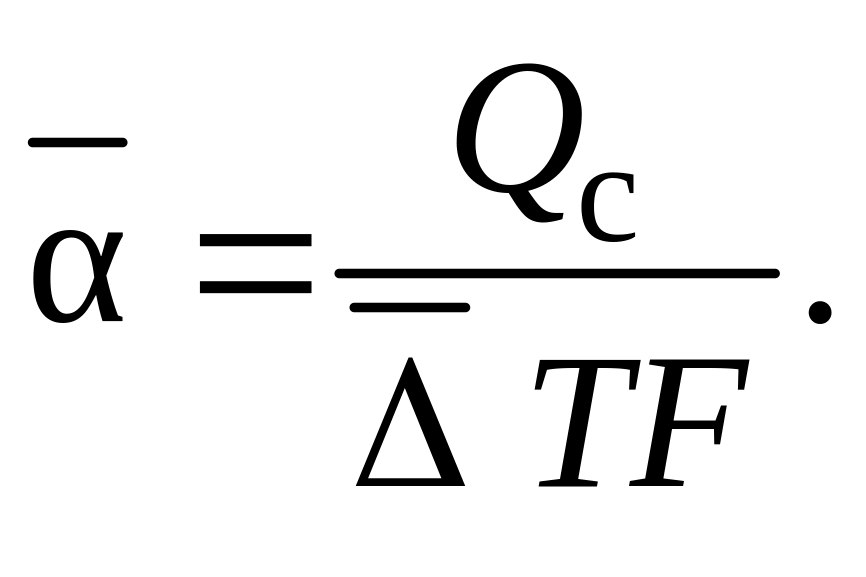(1.21)

Средний коэффициент теплоотдачи также имеет размерность Вт/(м²∙К).

Средний по поверхности коэффициент теплоотдачи и местные коэффициенты теплоотдачи могут быть связаны между собой

(1.22)

где F₀ – поверхность теплообмена, по которой проводится осреднение.

Если α является функцией лишь одной координаты, например x то формула (1.22) может быть упрощена

(1.23)

Если местный температурный напор ∆T является постоянной величиной по поверхности теплоотдачи, то формулы (1.22) и (1.23) примут вид

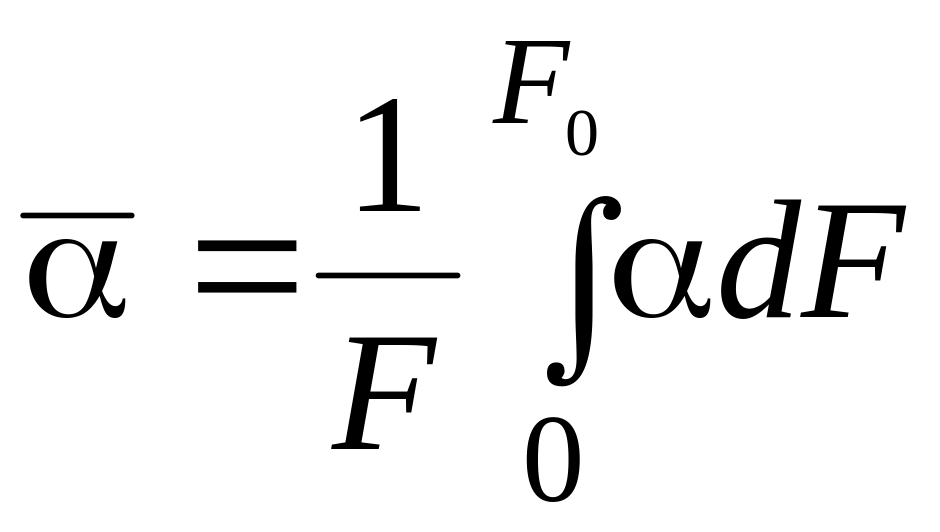; (1.24)

. (1.25)

Коэффициент теплоотдачи, как характеристика процесса теплоотдачи, определяющая ее интенсивность, зависит от многих факторов, оказывающих влияние на этот сложный процесс. В частности, α зависит от формы и размеров поверхности теплообмена, гидродинамических особенностей и характеристик движения среды, ее физических свойств и других факторов.

Из гидромеханики известно, что в непосредственной близости к обтекаемой потоком поверхности существует слой жидкости, в котором действует только молекулярный механизм переноса количества движения или импульса. Поперек этого слоя перенос теплоты осуществляется теплопроводностью, поэтому в соответствии с законом Фурье можно записать

(1.26)

где λ – коэффициент теплопроводности жидкости; n – внешняя нормаль к поверхности.

С другой стороны, согласно закону Ньютона-Рихмана,

q_c = α (T_c – T_ж). (1.27)

Поскольку оба уравнения определяют одну и ту же плотность теплового потока, можем записать

(1.28)

или

(1.29)

Равенства (1.28) и (1.29) описывают процесс теплоотдачи на границе, омываемой жидкостью поверхности теплоотдачи (стенки). Уравнение (1.29) называют уравнением теплоотдачи.