1.7.2 Ламинарный тепловой пограничный слой

Рассмотрим стационарный конвективный теплообмен вязкого потока с неизменными физическими характеристиками и умеренной скоростью. Внутренние источники теплоты в движущейся среде отсутствуют. Температура и скорость среды постоянные и во внешнем потоке соответственно равны Т₀ и U. Поверхность теплообмена (стенка) имеет постоянную и равномерно распределенную температуру Т_с. Характерный линейный размер поверхности l₀.

При принятой постановке задачи можно пренебречь кинетической энергией потока по сравнению с его энтальпией. Используем для анализа дифференциальное уравнение энергии, записанное в безразмерном виде.

Дифференциальное уравнение энергии для рассматриваемого случая записываем в безразмерном виде следующим образом:

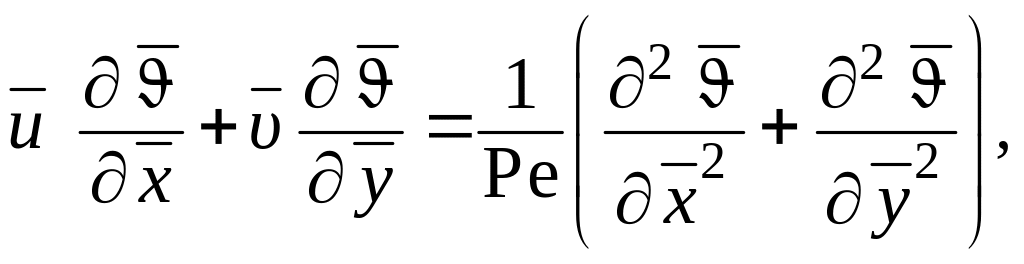(1.265)

Для дальнейших преобразований из физических соображений примем, что порядок толщины теплового пограничного слоя примерно равен порядку толщины гидродинамического пограничного слоя δ, O (δ_T) ≈ O (δ) (О – от латинского ordo – порядок). Причем в общем случае δ ≠ δ_T. Для безразмерных толщин и , где .

Оценим порядок членов исходного уравнения. В соответствии с ранее введенными понятиями (как и в уравнении движения в гидромеханике) считаем, что порядок продольной компоненты скорости в пограничном слое тот же, что и вне его, т.е. . Из тех же соображений для продольной и поперечной координат принимаем соответственно

Из уравнения сплошности

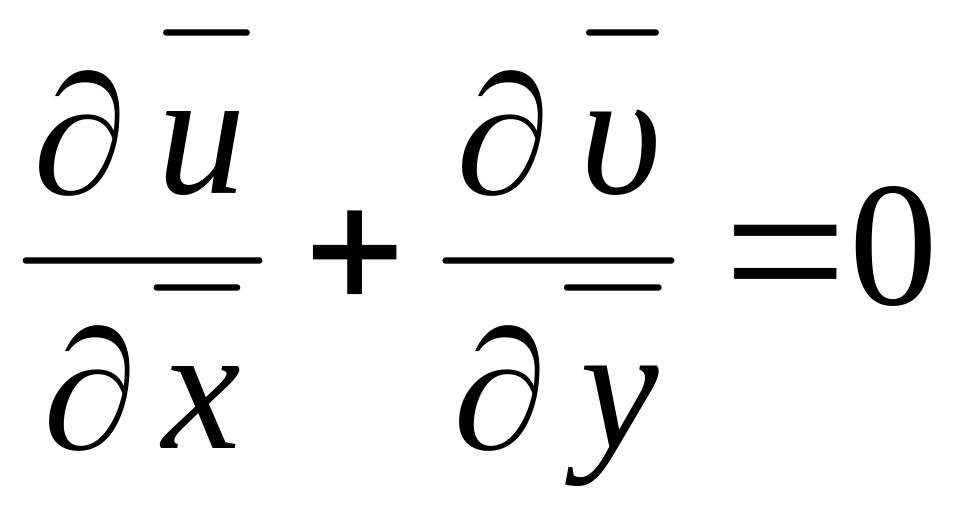(1.266)

следует, что

Порядки избыточных температур на поверхности теплообмена и внешнего потока примерно равны , поэтому

Для наглядности порядки членов исходного уравнения энергии запишем под каждым из них:

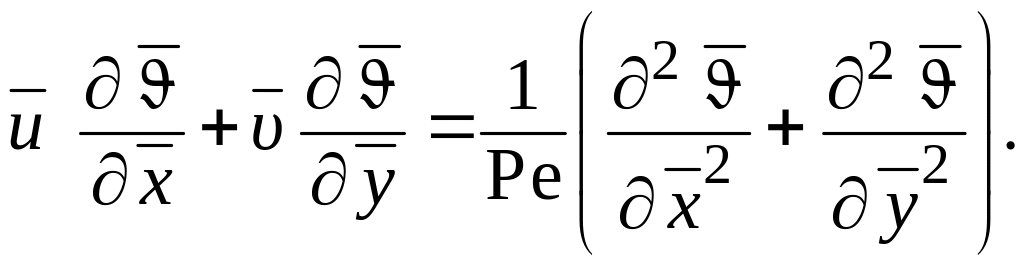
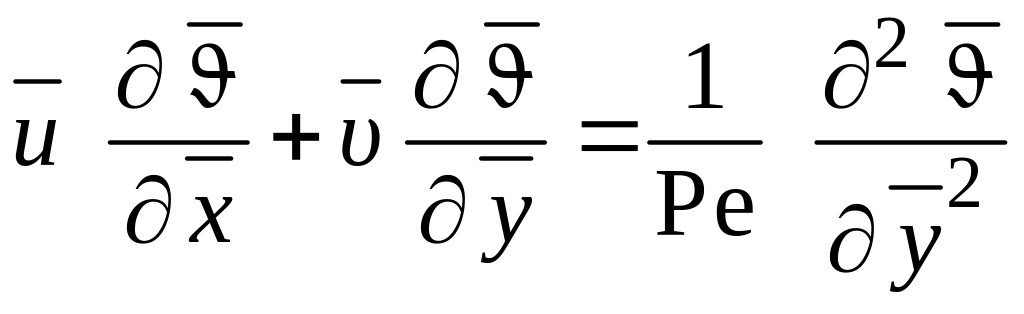. (1.267)

Полученное уравнение и является уравнением энергии для ламинарного пограничного слоя – уравнением ламинарного теплового пограничного слоя.

Порядок членов в его левой части равен единице, поэтому

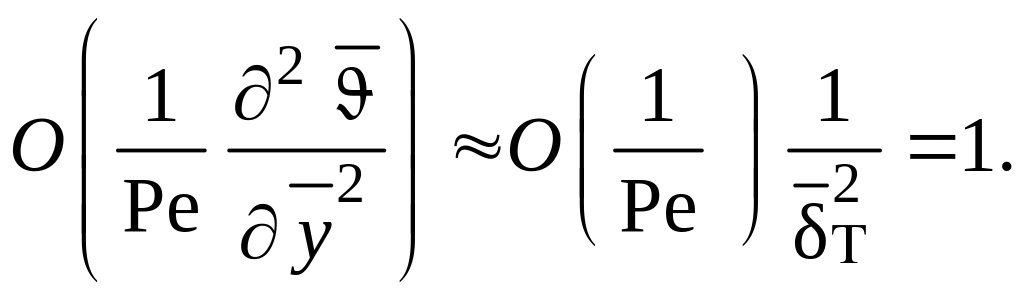(1.268)

Отсюда следует важное свойство ламинарного теплового пограничного слоя: толщина пограничного слоя есть величина порядка .

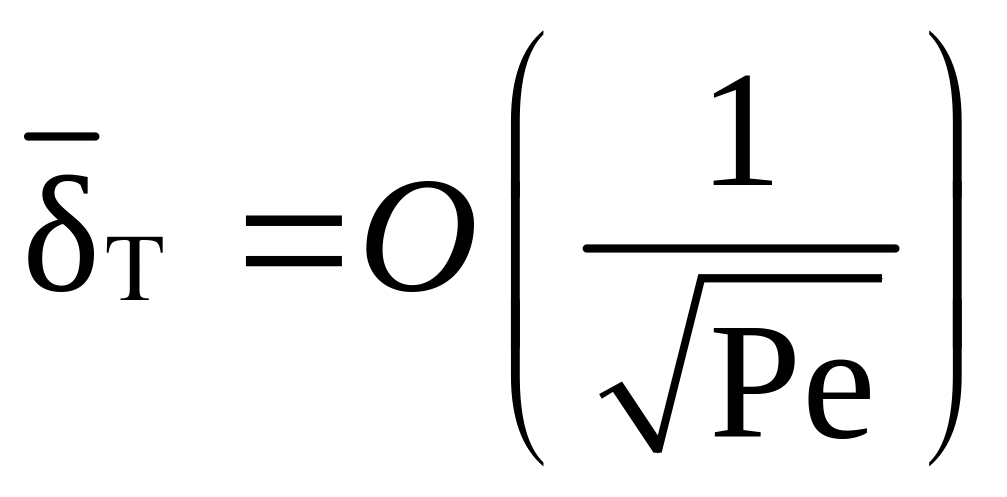. (1.269)

Напомним, что ранее для гидродинамического ламинарного пограничного слоя было установлено, что 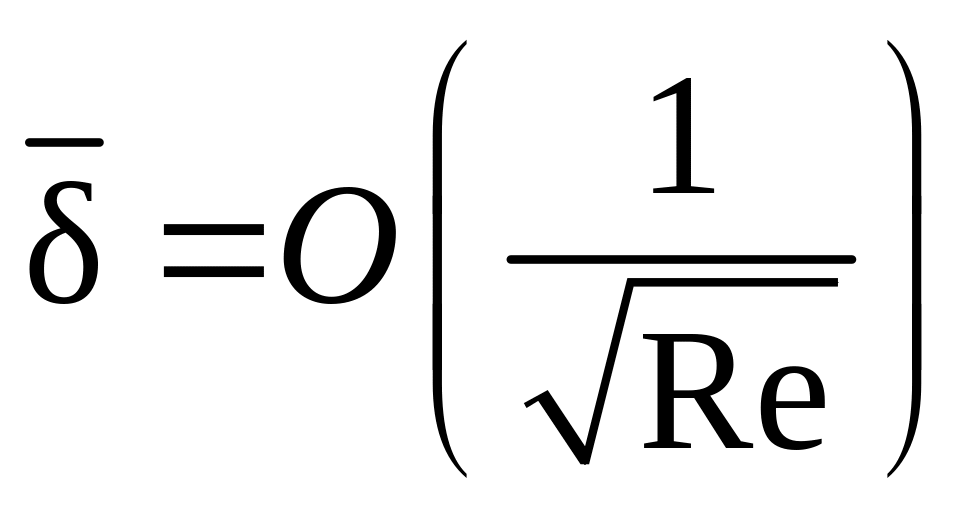(Re – число Рейнольдса). Поэтому

, (1.270)

или

, (1.271)

где Pr – число Прандтля.

На основании (1.271) можно утверждать, что соотношение между толщинами теплового и динамического ламинарных пограничных слоев определяется физическими свойствами среды, а критерий Прандтля является мерой этого соотношения. Таким образом, при Pr = 1 δ_T ≈ δ, при Pr > 1 δ_T < δ, при Pr < 1 δ_T > δ . Поскольку для капельных жидкостей обычно Pr ≥ 1, а для газов Pr ≈ 1 , то в приближенных технических расчетах можно считать, что δ_T ≤ δ.

Итак, уравнение энергии ламинарного теплового пограничного слоя в безразмерном виде может быть записано следующим образом:

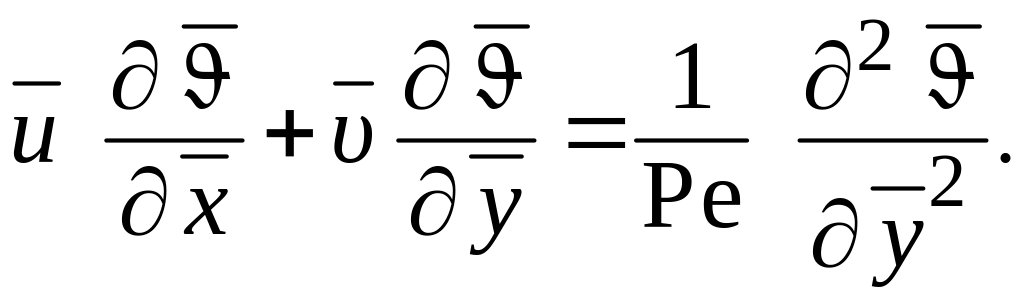(1.272)

Граничные условия при этом имеют вид

(1.273)

В размерном виде уравнение (1.272) и граничные условия (1.273) могут быть представлены так

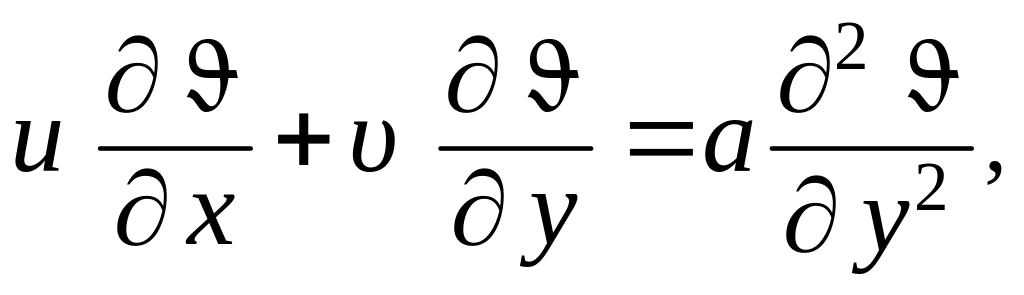(1.274)

(1.275)

Следует заметить, что характерным свойством теплового пограничного слоя является неизменность вдоль течения температуры на его внешней границе, т.е. постоянство ( ). Напомним, что для гидродинамического пограничного слоя в общем случае скорость на его внешней границе зависит от продольной координаты, т.е. .

Сопоставляя уравнения теплового и гидродинамического ламинарных пограничных слоев, можно заметить, что они будут иметь аналогичный вид в случае безградиентного движения потока, т.е. при 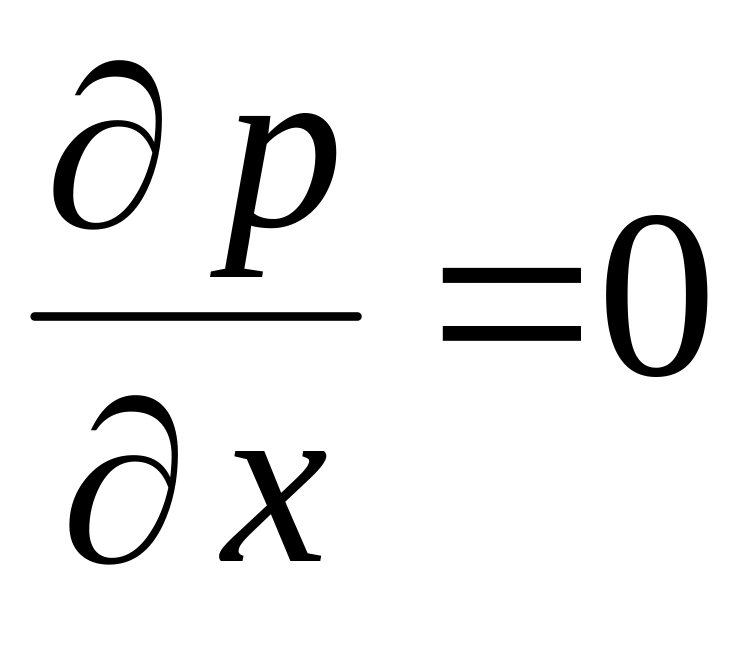(обтекание плоской поверхности). Оба уравнения (для гидродинамического пограничного слоя записываем только основное уравнение) могут быть представлены следующим образом:

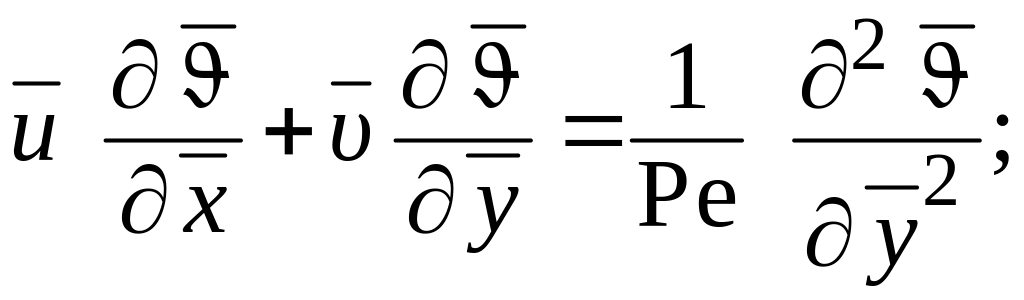(1.276)

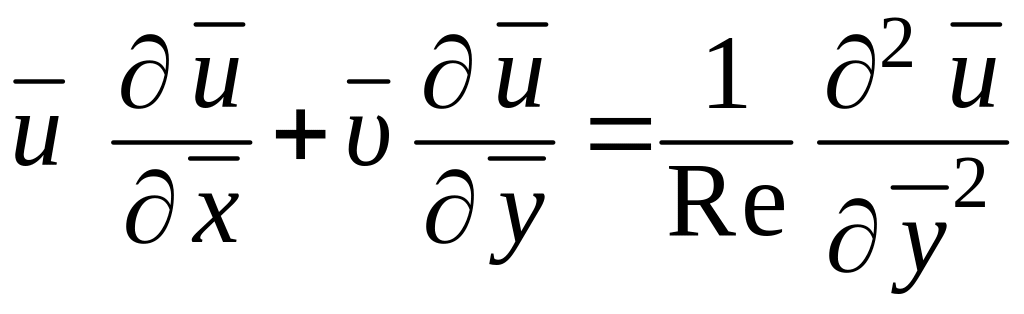. (1.277)

Граничные условия:

(1.278)

Отсюда видно, что при безградиентном течении число Пекле выступает аналогом числа Рейнольдса.

При приближенных методах решения задач теплового пограничного слоя, как и гидродинамического, используются не уравнения пограничного слоя, а интегральные соотношения.

Левую часть уравнения (1.274) записываем в виде

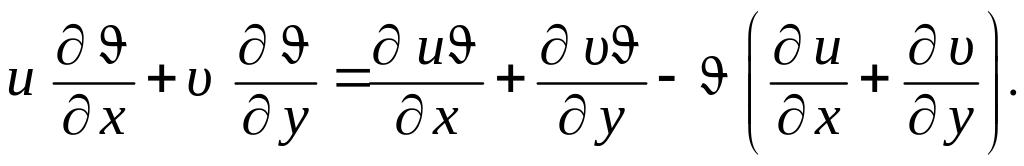(1.279)