4.5. Цепь с индуктивностью

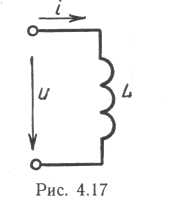
В электрической цепи (рис. 4.17) действию перемен­ного напряжения и создаваемого им тока противодей­ствует ЭДС самоиндукции e_L = — Ldi/dt. При этом в лю­бой момент времени ток имеет такое мгно­венное значение, при котором противодейст­вие равно действию, т. е. и= — е.

В моменты времени, когда ток достига­ет

амплитуды i = I_m, скорость его измене­ния

di/dt = O (ток перестал увеличиваться,

в следующий момент времени он

начнет уменьшаться), поэтому e_L=0_tu= — £/,=0.

Значит, синусоидальные напряжения и ток

сдвинуты по фазе на 90°.

Фактором, сдвигающим ток по фазе, является

ЭДС самоиндукции.

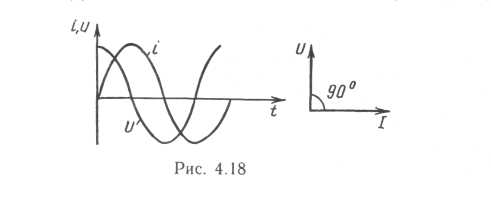
Изменение тока катушки индуктивности происходит за счет изменения напряжения. Появление напряжения — причина возникновения тока катушки. Поэтому на индуктивности ток отстает от напряжения на угол 90° (1) (рис. 4.18).

Примем i = I_m sin ωt . Тогда и = — e_L = Ldi/dt = Ld (I_m sin ωt) / dt = ωLI_m cos ωt = U_m sin ( ωt + 90°), что подтверждает положение (1) и дает выражение U_m = ωLI_m. Разделив его на √2, имеем U = ωLI ,

от­куда

I=U/(ωL)=U/X_L; (4.7)

X_L =ωL=2 πfL; X_L = U/I. (4.8)

Формула (4.7) отражает закон Ома для участка цепи с индуктивностью, а (4.8) позволяет рассчитать индук­тивное сопротивление.

По аналогии с емкостным сопротивлением значение индуктивного сопротивления нельзя относить к мгновен­ным значениям тока и напряжения.

При i = I_m di/dt = 0, поэтому e_L = — Ldi/dt = 0.

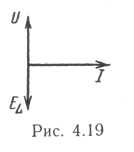
Зна­чит, ЭДС самоиндукции отстает от тока по фазе на 90° (рис. 4.19). Учитывая, что напряжение опережает ток по фазе на угол 90°, делаем вывод, что в цепи с индуктивностью напряжение и ЭДС самоиндукции находятся в противофазе, т. е. ЭДС самоиндукции уравновешивает действие напряжения (2).

Мгновенное значение мощности р=иi в цепи с индуктивностью непрерывно изменя­ется.

Подобно конденсатору, индуктивность обменивается энергией с источником так, что средняя мощность за период (активная мощность) равна нулю, а реактивная индуктивная мощность Q_L, подобно реактивной емкостной мощности, равна амплитудному значению мгновенной мощности:

Q_L==UI = I²X_L.

4.6. Цепь при последовательном соедине­нии активного и индуктивного сопротив­лений

Расчеты цепей переменного тока проводят не для мгновенных, а для действующих значений токов и напря­жений, которые в дальнейшем будем называть ток и на­пряжение.

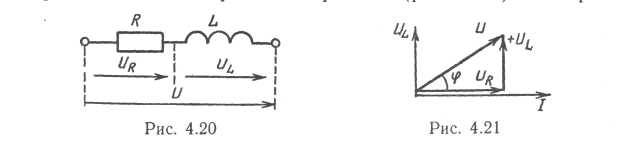
Для цепи переменного тока справедливо положение (3). При этом создаваемые током падения напряже­ний U_R = IR и U_l = IXl совместно противодействуют напряжению источника.

Если бы U_R и U_L совпадали по фазе, то U=U_R+Ul = 140 В. Докажем, что они не совпадают по фазе, при помощи векторной диаграммы (рис. 4.21). Построение диаграммы начинаем с вектора тока, так как он одинаков для обоих участков.

К нему пристраиваем век­тор U_R , совпадающий по фазе с током на активном сопро­тивлении (см. рис. 4.10), и вектор U_L, опережающий ток по фазе на 90° на индуктивном сопротивлении (см. рис.4.18). Получаем, что векторы U_R и U_L сдвинуты между собой по фазе на 90°. Складывая их, находим резуль­ тирующее напряжение цепи:

U= U²_R+ U² _L (4.9)

В цепи, имеющей, кроме индуктивного, активное сопро­тивление, напряжение опережает ток на угол, значение которого меньше, чем 90°(1).

Из уравнения (4.9) U=√I² R² + √I² X² _L = I√R² + √X² _L = IZ,

где Z – полное сопротивление цепи:

Z = R ² + X ² _L ; (4.10)

I=U/Z. (4.11)

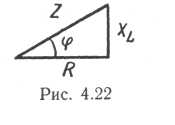
Формула (4.11) отражает закон Ома, а (4.10) позво­ляет вычислять полное сопротивление цепи. Разделив стороны треугольника напряжений (выраженные в едини­цах напряжения) (рис. 4.21) на ток, получаем треуголь­ник сопротивлений (рис. 4.22), из которого

R= Z cos φ; X_L = Z sin φ. (4.12)

Активная мощность рассматриваемой цепи P = I²R, реактивная

Ql = I²X_l. Полная мощность цепи S = I²Z.

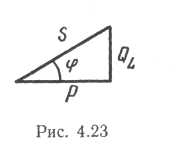
У множив стороны треугольника напряжений (выра­женные в единицах напряжения) на ток, получаем тре­угольник мощностей (рис. 4.23), из которого

S = UI, S = P² + Q²_L ; (4.13)

P = S cosφ = UI cosφ; (4.14)

Q = S sin φ == UI sin φ. (4.15)

За единицу активной мощности принят ватт (Вт), реактивной — вольт-ампер реактивный (вар), полной — вольт-ампер (В • А).

Из формул (4.12), (4.15) можно определить cosφ или sinφ , а затем угол φ, который является углом сдвига фаз между током и напряжением. Этот угол можно также найти из рис.4.21, 4.22, 4.23. Во всех треугольниках он одинаковый, так как треугольники подобные.