4.3. Цепь с активным сопротивлением

В электрической цепи (рис. 4.9) действию перемен­ного напряжения и и создаваемого им тока оказывает противодействие падение напряжения iR на активном сопротивлении, т. е. в любой момент времени и = iR.

В соответствии с положением (2) активное сопротивление численно равно падению напряжения, создаваемому током один ампер и оказывающему про­тиводействие этому току. Падение напряжения, созда­ваемое мгновенным значением тока i, равно

u = iR, амплитудным значением тока I_m, U_m = I_mR, действую­щим значением тока I, U = IR. Отсюда

i = u/R; I_m = U_m/R; I=U/R.

Эти формулы отражают закон Ома для мгновенных, амплитудных и действующих значений тока и напря­жения.

Примем фазу тока аi = ωt, i = I_m sinωt (рис. 4.10).

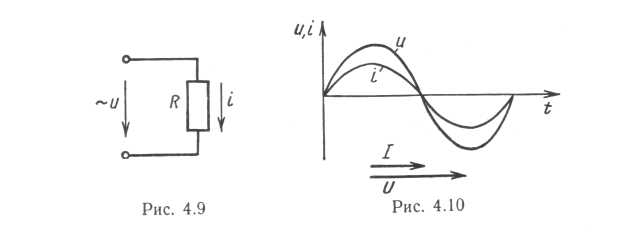
Тогда u = iR = I_mR sin ωt = U_m sin ωt , т. е. фаза напря­жения равна фазе тока: а_и = ωt = a_i. На активном сопро­тивлении ток и напряжение совпадают по фазе (1).

4.4.Цепь с емкостью

В электрической цепи (рис. 4.14) действию перемен­ного напряжения и оказывает противодействие падение напряжения на конденсаторе и_с, создаваемое током. При этом мгновенное значение тока i, изменяющее заряд конденсатора q, такое, что создаваемое этим зарядом напряжение конденсатора в любой момент времени урав­новешивает действие напряжения цепи, т. е. и_с=и.

В моменты времени, когда конденсатор полностью заря­жен, и_с = и_т, i = 0 (ток перестал заряжать конденса­тор, в следующий момент времени конденсатор будет разряжаться). Значит, синусоидальный ток и напряжение сдвинуты по фазе на 90°. Фактором, сдвигающим по фазе ток, является напряжение электрического поля за­рядов конденсатора.

Изменение напряжения на обкладках конденсатора происходит за счет изменения тока. Ток — причина возникновения напряжения конденсатора, напряжение — следствие. Поэтому на емкости ток опережает напряже­ние по фазе на угол 90° (1) (рис. 4.15).

Примем и = U_msinωt. Используя формулы (2.1) и (1.6), получаем

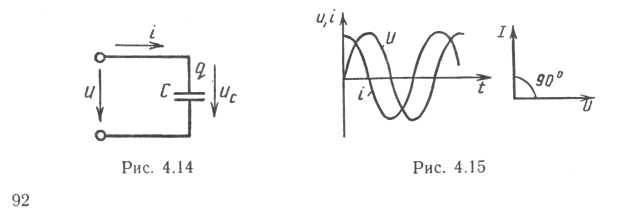
i = dq/dt = Cdu/dt = Cd(U_m sin ωt)/dt = ωCU_m cos ωt =I_m sin (ωt + 90°), что подтверждает по­ложение (1) и дает выражение I_m = U_mωC. Разделив его на √2, имеем I = UωС, откуда I = U/X_C , где

Xс = 1/(ωС).

I=U/X_C; (4.5)

Х_с = 1/(ωС)= 1 /(2πfС); Х_с = U/I. (4.6)

Формула (4.5) отражает закон Ома для участка цепи с емкостью, а (4.6) позволяет рассчитать емкостное сопротивление.

В формуле (4.5) значение Х_с относится к действую­щим значениям тока и напряжения. Для мгновенных значений тока эту формулу применить нельзя, так как, например, в моменты времени, когда конденсатор раз­ряжен, q = 0, и = 0, i = I_m (рис. 4.15), а по фор­муле получилось бы i = и/Хс = 0/Х_с = 0, что непра­вильно.

В цепи с емкостью мгновенное значение мощ­ности р = ui непрерывно изменяется по графику pit) (рис. 4.16).

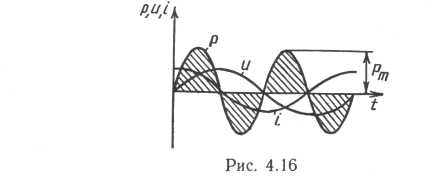
При зарядке конденсатор потребляет энергию, при разрядке отдает ее назад в цепь, поэтому среднее зна­чение мощности за период (т. е. активная мощность) равно нулю. Для количественной характеристики интен­сивности обмена энергией между источником и конден­сатором введено понятие реактивной мощности Q_c , которая равна максимальному значению мгновенной мощности

p= иi = U_m sin ωt ·I _m cos ωt = U_m I_m /2 · sin 2ωt = UI sin 2ωt = Q_c sin 2ωt , т.е.

Q_c =UI = I² X_c