
- •Математика
- •Оглавление
- •Введение
- •1. Введение в математический анализ
- •1.1. Способы задания функций
- •1.2. Способы образования функций
- •1.3. Предельные процессы переменной X
- •1.4. Предел функции. Бесконечно малые и бесконечно большие функции
- •1.6. Раскрытие неопределенностей вида
- •1.8. Непрерывность и разрывы функции
- •2. Дифференциальное исчисление функций одной переменной
- •2.1. Понятие производной
- •2.2. Правила дифференцирования. Дифференциал функции
- •2.3. Производные высших порядков
- •2.4. Правило Лопиталя
- •2.5. Уравнение касательной и нормали
- •2.6. Исследование функций на монотонность (возрастание, убывание) и экстремум
- •2.7. Нахождение наименьшего и наибольшего значений функции
- •2.8. Исследование графиков функций на выпуклость, вогнутость и перегиб
- •2.9. Полное исследование функций и построение графиков
- •Список рекомендуемых источников
- •Приложение
1.2. Способы образования функций
Самыми простыми среди явно заданных функций являются 16 функций:
1) y = С — постоянная;
2) y = xn — степенная (n 0);
3) y = ax — показательная (a > 0, a 1);
4) y = loga x — логарифмическая (a > 0, a 1);
5) y = sin x, y = cos x, y = tg x, y = ctg x, y = sec x, y = cosec x — тригонометрические;
6) y = arcsin x, y = arccos x, y = arctg x, y = arcctg x, y = arcsec x, y = arccosec x — обратные тригонометрические функции.
Эти функции называют основными элементарными функциями. Свойства и графики этих важных функций изучают в курсе математики средней школы. Эти сведения желательно повторить. Для этого можно использовать школьные учебники, а также [2, § 14].
Из основных элементарных функций, как из «кирпичиков», образуют множество новых функций. Для этого используют различные способы. Рассмотрим некоторые из них.
1. Образование функций с помощью арифметических операций (+, –, , :), например:
а) y = 3 sin x + 4 tg x – 5 lg3x + arcsin x;
б) Pn(x) = a0xn + a1xn-1 + …+ an-1x + an — многочлен степени n;
в) гиперболические функции:
![]() —
гиперболический
синус;
—
гиперболический
синус;
![]() —
гиперболический
косинус;
—
гиперболический
косинус;
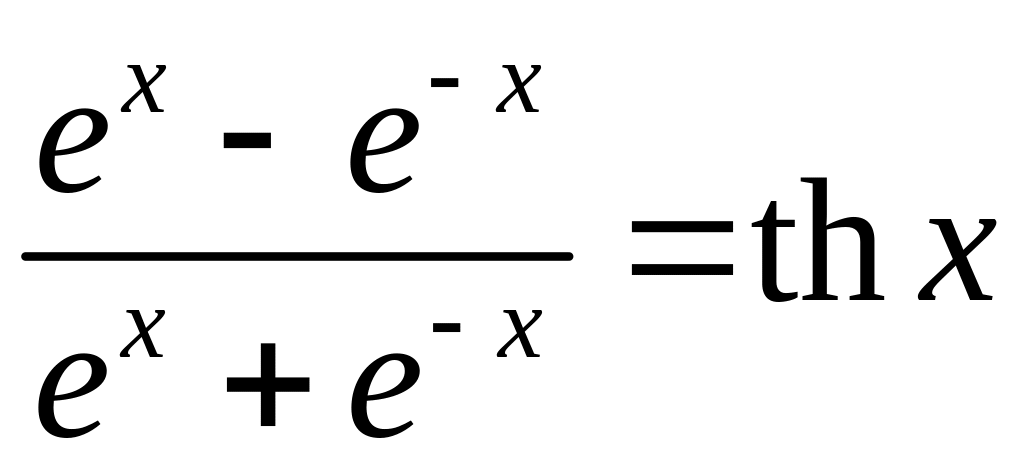 —
гиперболический
тангенс;
—
гиперболический
тангенс;
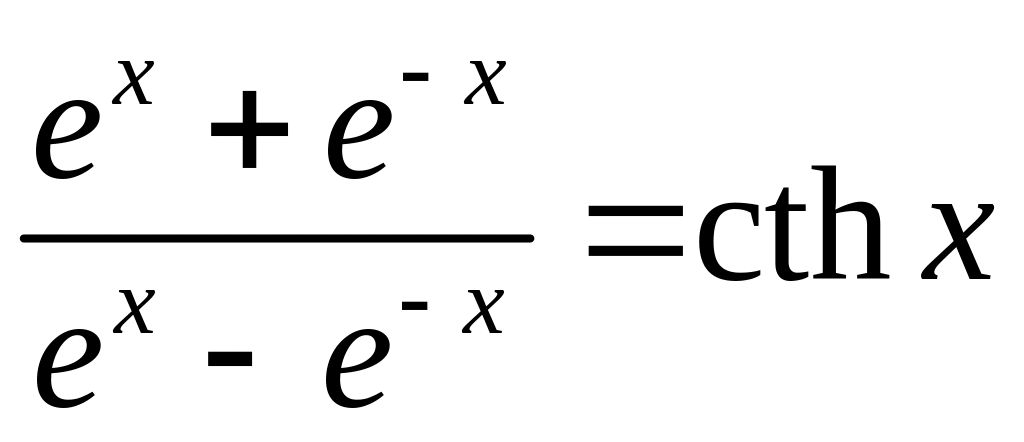 — гиперболический
котангенс.
— гиперболический
котангенс.
Заметим, что гиперболические функции получены с помощью арифметических операций из показательной функции аx при a = e.
2. Образование функций с помощью повторного взятия функции:
y = f((x)). (1)
Такую функцию называют сложной функцией или функцией сложного аргумента. Например, сложными будут функции:
y = sin 3x, y = arctg (lg x), y = lg (x2 + 1), (2)
а их аргументами, соответственно, 3x, lg x, x2 + 1.
3. Образование функций с помощью нескольких аналитических выражений, например
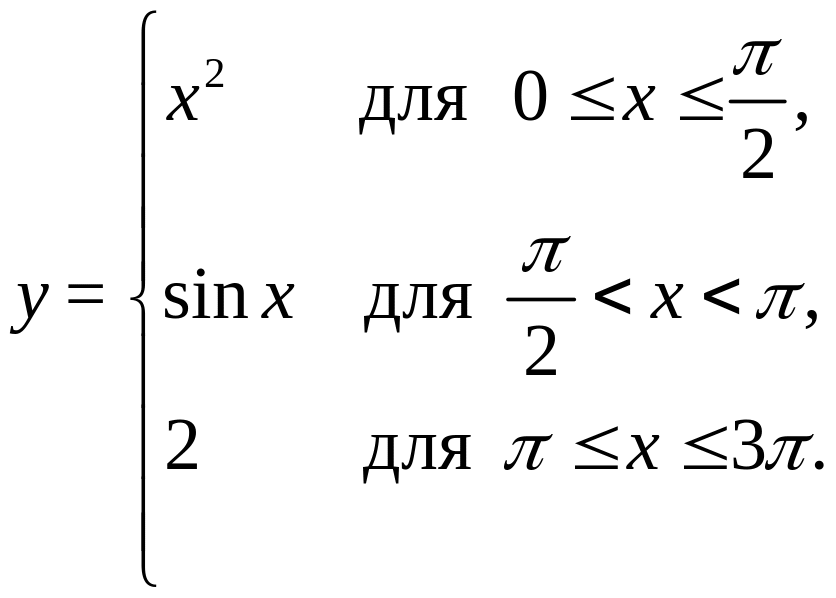 (3)
(3)
Эта функция в области D(y) = [0; 3] задана тремя различными аналитическими выражениями.
При образовании функций могут использоваться и другие, кроме перечисленных выше, операции, например, дифференцирование и интегрирование, а также бесконечное число таких операций. Из множества подобных функций выделяют наиболее простые — те, которые получены из основных элементарных функций с помощью конечного числа арифметических операций и операций взятия функций от функций и которые записаны одним аналитическим выражением. Такие функции называют элементарными. Например, элементарными будут многочлены, гиперболические функции, функции (1) и (2), а функция (3) не будет элементарной, так как она задана не одним аналитическим выражением.
1.3. Предельные процессы переменной X
При изменении переменной величины x иногда можно выделить характерную особенность в ее поведении: монотонное возрастание или убывание, неограниченное приближение к постоянному числу и т.п. Если переменная величина x (например, время) неограниченно возрастает и при этом остается положительной, то такое поведение величины x символически будем обозначать как x +. Таким образом, символическая запись x + будет означать, что x неограниченно возрастает и в процессе изменения станет и останется больше любого сколь угодно большого числа М > 0. Итак, x + — это один из предельных процессов поведения переменной x. Аналогично понимаются другие предельные процессы:
x –,
x | x| +,
x a — x неограниченно приближается к числу а,
x
a
–
0
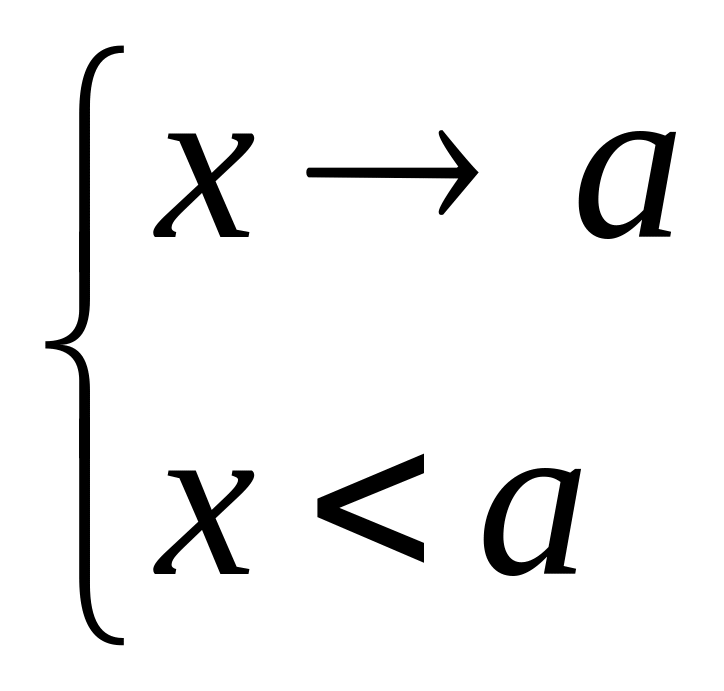 — x
неограниченно приближается к а
слева;
— x
неограниченно приближается к а
слева;
x
a
+ 0
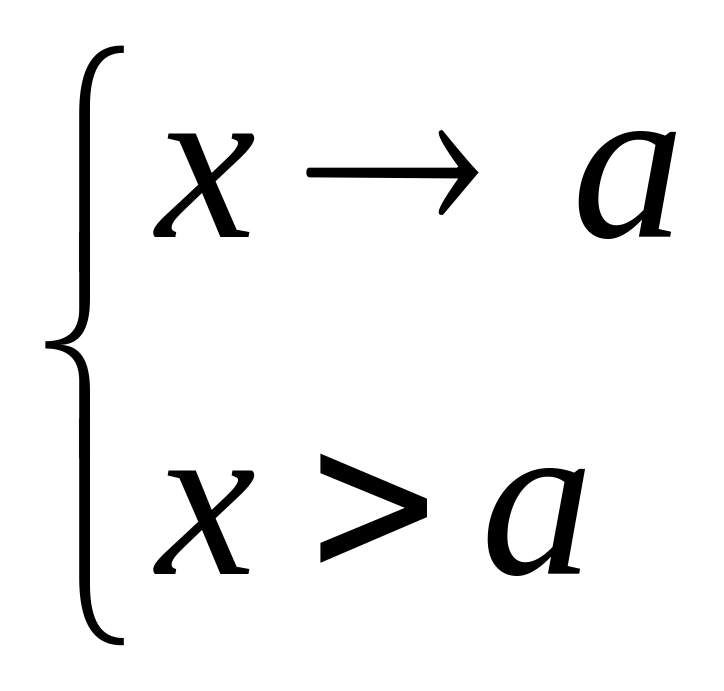 —
x
неограниченно приближается к а
справа.
—
x
неограниченно приближается к а
справа.
