Расчет прочности нормальных сечений

Продольная рабочая арматура в рёбрах принята в соответствии с заданием класса А400, расчётное сопротивление R_s=350 МПа (таблица Приложения «В»). Сечение тавровое с полкой в сжатой зоне представлено на рисунке 5; расчетная ширина полки b´_f = B = 1525 мм; h′_ƒ =50мм, h₀ = h – a = 350 – 55 = 295 мм .

Рисунок 5 – Расчётное сечение продольного ребра по прочности

Полагая, что нейтральная ось лежит в полке, α_m и ξ будут равны:

;

;

Проверка условия:

x = h₀ = 0,114 295 = 33.61мм < h_f=50 мм;

_<

Площадь сечения продольной арматуры:

Принимаем продольную арматуру 222 А400+220 А400 с А_s= 1388 мм² (+10.3%) по два стержня в каждом ребре.

Расчёт нормальных сечений к продольной оси элемента по деформационной модели

Расчет по прочности производят из условий:

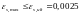
Деформации в продольной арматуре в предельном состоянии при двузначной эпюре деформаций согласно гипотезе плоских сечений равны:

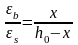откуда, ,

где: х – фактическая высота сжатой зоны бетона:

где: х₁ – высота сжатой зоны при прямоугольной эпюре напряжений, полученная при расчёте по предельным усилиям. Используя расчёты, выполненные выше (х₁=33.61 мм, h₀=295 мм), и задавшись , проверим предельные деформации в бетоне:

- деформации в бетоне не превышают предельных.

Расчет прочности наклонных сечений на поперечную силу

Поперечная сила на грани опоры Q_max = 92,3 кН. В каждом продольном ребре устанавливается по одному каркасу с односторонним расположением двух рабочих стержней диаметром d = 22 мм (рис.3,5). Диаметр поперечных стержней из условия требований свариваемости должен быть не менее 0,25 диаметра продольной арматуры. В данном случае принимаем поперечные стержни диаметром d_sw= 6 мм > 0,25∙22 = 5,5 мм из арматуры класса А240,

A_sw1=28,3 мм²; расчетное сопротивление R_sw = 170 МПа. При A_sw1=28,3 мм² и n = 2 (на оба ребра) имеем: A_sw = n A_sw1=228,3 = 56,6 мм².

Бетон класса В15 (R_b = 8,5 МПа; R_bt = 0,75 МПа; коэффициент условий работы бетона γ_b1=1,0 т.к. кратковременная нагрузка составляет более 10% от всей временной нагрузки).

Предварительно принятый шаг хомутов:

S_w1 = 75 мм (S_w1 ≤ 0,5h₀ = 0,5 ∙ 295 = 147,5мм; S_w1≤300мм)

S_w2= 200мм (S_w2 ≤ 0,75h₀ = 0,75 ∙ 295 = 222 мм; S_w2≤500мм)

Прочность бетонной сжатой полосы из условия:

, то есть прочность полосы обеспечена.

Интенсивность хомутов определяется по формуле (13) [10]:

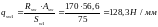
Поскольку q_sw1 = 128,3 Н/мм > 0,25R_вt·b = 0,250,75185 =34,69 Н/мм – хомуты учитываются в расчете и значение М_b определяется по формуле:

Самая невыгодная длина проекции наклонного сечения C определяется из выражений:

Поскольку , значение С определяется по формуле:

> 3h₀=295=885 мм,

Принято С = 3h₀ = 885мм.

Длина проекции наклонной трещины С₀ принимается не более С и не более 2h₀. В данном случае с₀ = 2h₀ = 2  295 = 590 мм. Тогда

.

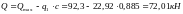Проверяем условие (8) [10]:

кН > (+6,5%),

т.е. прочность наклонных сечений обеспечена

Проверка требования:

> S_w1=100 мм.

т.е. требование 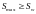выполнено.