1.3 Расчёт приближенным методом Циглера – Никольса

А) (вручную)

В 1942 году Циглер и Никольс впервые предложили следующую последовательность настройки регуляторов.

Предполагаемый коэффициент затухания ψ =0,7...0,8. Динамика объекта регулирования неизвестна.

Сначала настраивают регулятор как П-регулятор, увеличивая коэффициент усиления P до достижения незатухающих колебаний, т.е.достижения границы устойчивости.

Фиксируют как критические период колебаний Tкр и достигнутый коэффициент усиления Pкр .

Определяют оптимальные настройки регуляторов:

П-регулятора P = 0,55 Pкр.

ПИ-регулятора P = 0,45 Pкр и I опт =0,54 * Ркр / Ткр

ПИД-регулятора соответствует P= 0,6 Pкр, I = 1,2*Ркр/Ткр и D = 0,075*Ркр*Ткр.

Предложенная Циглером и Никольсом методика дает хорошие осредненные результаты.

Недостаток – необходимость выведения системы на границу устойчивости, наличия системы регистрации.

Б) (аналитически)

В соответствии с этим методом расчёт настроек ПИ- или ПИД- регуляторов проводят в два этапа:

• расчет критической настройки пропорциональной составляющей С1кр (С0 = 0, С2 = 0 ), при которой АСР будет находится на границе устойчивости и соответствующую ей критическую частоту

• определение по С1кр и оптимальных настроек С0, С1, С2, обеспечивающих степень затухания

З ная передаточную функцию объекта С1кр и ωкр можно определить аналитически:

Тогда, решая систему уравнений, получим:

Оптимальные настройки регуляторов находятся по формулам (P=C1, I=C0, D=C2):

П – регулятор С1 = 0,5∙С1кр . (1.5)

ПИ – регулятор С1 = 0,5∙С1кр ; (1.6)

С0 = 0,086∙С1кр . .

П ИД – регулятор С1 = 0,6∙С1кр ;

C0 = 0,192∙С1кр∙ωкр ; (1.7)

Метод Циглера —Никольса лежит в основе многих методов настройки дискретных ПИД – регуляторов.

Метод Циглера–Никольса

Задача 1

Расчитать систему автоматического регулирования температуры мазута в смешивающем теплообменнике. Мазут подогревается паром с помощью барботера. Температура регулируется подачей пара в барботер. Расход мазута остается неизменным.

Передаточная функция по каналу регулирования равна

Функциональная схема представлена на рисунке 1.3

Рисунок 1.3 - Схема регулирования температуры

Решение:

АСР представляет собой одноконтурную АСР . Температура регулируется путем изменения расхода пара

Структурная схема представлена на рисунке 1.4

Рисунок 1.4 – Структурная схема АСР регулировки температуры

Для расчёта параметров ПИД -регулятора , и воспользуемся формулами из таблицы 1.2:

где: - мнимая и реальная части обратной расширенной амплитудно-фазовой характеристики объекта соответственно.

Пусть колебательность системы равна 0.221, что соответсвует степени затухания порядка 0.75.

Далее, задаваясь значениями , построим поверхность равной степени затухания, так как регулятор имеет три параметра настройки. Для этого составим программу в Matlab через меню File (см. рисунок ниже)

.

Рисунок – Выбор пункта меню для создания m-файла

Программа для расчёта настроек ПИД-регулятора на ЭВМ имеет следующий вид:

****************************************************************************

function Z

i=0;% вспомогательные переменные цикла

j=0;

w=0.01; % заданная частота

m=0.221;% заданная колебательность системы

while j<19

j=j+1;

C22(j)=j/5 ; % задаем значения произвольно для С2

i=0;

while i<19

p=(-m+1i)*w*i; i=i+1; %замена переменной через частоту «омега» и колебательность m

A=4*exp(-p*4)/(80*p*p+18*p+1); %передаточная функция

A0=1/A; %находим обратную передаточную функцию

C1(j,i)=m*imag(A0)-real(A0)+2*m*w*C22(j); %кодируем формулу, взятую из таблицы для С1

C0(j,i)=w*i*(m^2+1)*(imag(A0)+w*C22(j));% кодируем формулу для С0

C2(j,i)=C22(j); %запоминаем значение С2

end

end

surfl(C1,C2,C0),%grid;

colorbar

********************************************************************************

В результате расчета получаем поверхность равной степени затухания изображенной на рисунке 1.5.

Рисунок 1.5 – Поверхность равной степени затухания

Любая точка лежащая на этой поверхности соответствует степени затухания . Задаваясь значением С2=3, получим сечение этой поверхности ( смотри рисунок 1.6). Для этого модифицируем скрипт программы:

*********************************************************************************

function ZZ

i=0;% вспомогательные переменные цикла

j=0;

w=0.01; % заданная частота

m=0.221;% заданная колебательность системы

C2=3;% фиксируем C2 = 32

while j<19

j=j+1;

p=(-m+1i)*w*j; %замена переменной через частоту «омега» и колебательность m

A=4*exp(-p*4)/(80*p*p+18*p+1); %передаточная функция

A0=1/A; %находим обратную передаточную функцию

C1(j)=m*imag(A0)-real(A0)+2*m*w*C2; %кодируем формулу, взятую из таблицы для С1

C0(j)=w*j*(m^2+1)*(imag(A0)+w*C2);% кодируем формулу для С0

end

plot(C1,C0);

****************************************************************************

На этом сечении выберем настройки С1иС0.

Рисунок 1.6 – Сечение поверхности равной степени затухания плоскостью С2=3

Многочисленные промышленные опыты настройки регуляторов показывают, что следует выбирать С0 и С1 лежащие несколько правее максимума кривой заданного затухания (рисунок 1.6).

В данном расчете наиболее благоприятным переходным процессом является процесс при следующих настройках ПИД-регулятора С2=3 С0 = 0,0475 и С1 = 0.03652

Модель системы представлена на рисунке 1.7, а переходной процесс, полученный в результате моделирования на рисунке1.8.

Рисунок 1.7 – Модель системы регулирования температуры

Рисунок 1.8– переходной процесс в системе регулирования температуры

В результате проведенных операций мы рассчитали систему регулирования на заданную степень затухания

Задача 2

Дана автоматическая система регулировки уровня функциональная схема которой представлена на рисунке1.9

Рисунок1.9 – Функциональная регулировки уровня

Исходные данные:

,

где k = 0.7 ;=2; Т2 = 5 ; Т1 = 11.

Требуется рассчитать настройки ПИД регулятора.

Решение:

АСР уровня представляет собой одноконтурную АСР. Структурная схема представлена на рисунке1.10

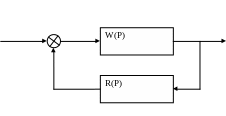
Рисунок 1.10 – Структурная схема АСР регулировки уровня

Передаточная функция объекта имеет следующий вид:

Для определения критической настройки регулятора все настройки регулятора приравнивают к нулю, а затем постепенно добавляя значение С1, выводят систему автоматического регулирования на грань устойчивости. Настройка, при которой система будет находиться на грани устойчивости и будет являться критической.

Определим настройки ПИД – регулятора с помощью программы выполненной в Матлабе.

Листинг программы:

function PID

w = 0.01

tau=2;

K=0.7;

i=0;

while i<=1000

p=(+1i)*w*i; i=i+1;

W=K/(55*p*p+16*p+1)*exp(-tau*p);

A =W;

AO(i)= real(A);

A1(i)=imag(A);

if A1(i)>0

wkr=w*i; C1kr=-1/AO(i); i=500001;

end

end

i=10

plot(AO,A1)

C1 = 0.6*C1kr

C0 = 0.192*C1kr*wkr

C2 = 0.471*C1kr/wkr

wkr=wkr

C1kr=C1kr

Полученные настройки ПИД - регулятора:

С1=7.5546;

С0=0.9186;

С2=15.6;

кр кр=0.38.

С1кр=12.591

Модель системы представлена на рисунке 1.11

Рисунок 1.11 – Модель системы регулирования уровня

Переходная характеристика, полученная в результате моделирования, представлена на рисунке1.12

Рисунок 1.12– переходная характеристика

Время регулирования согласно графика переходного процесса составляет 45с.

Перерегулирование составит:

А фактическая степень затухания:

Таким образом, в результате проведенных операций, мы рассчитали систему регулирования на заданную степень затухания , что соответствует теоретическим характеристикам метода Циглера-Никольса. Обратите внимание, несмотря на то, что степень затухания «хорошая», а перерегулирование все таки остается недопустимым, то есть выше 30%.

В заключении воспользуетесь

Контрольные вопросы

1. Какие критерии качества используют при расчете одноконтурных АСР?

2. Дайте определение степени затухания переходного процесса.

3. Дать определение расширенной частотной характеристики.

4. В чем заключается суть метода расчета с помощью расширенных частотных характеристик?

5. Пояснить расчет одноконтурной АСР методом незатухающих колебаний.

6. Записать значение передаточных функций ПИ и ПИД регуляторов.