Самостоятельная работа № 1

Тема: «Нахождение приближенного значения величины, вычисление погрешности приближений»

Цель: научиться находить погрешности вычислений;

научиться округлять числа;

Для выполнения данной работы студент должен знать:

1. определение абсолютной и относительной погрешностей;

2. правило округления и записи приближенных чисел.

Уметь:

1. использовать формулы погрешностей при проведении вычислений;

2. использовать правила округления и записи приближенных чисел.

Ход работы:

1. Изучите краткое содержание материала и выпишите следующие формулы:

1. абсолютной погрешности;

2. предельной абсолютной погрешности;

3. относительной погрешности;

4. предельной абсолютной погрешности.

2. Выпишите определения верных и значащих цифр;

3. Повторите правила округления чисел.

Краткое содержание материала

1. Приближенное значение величины. Абсолютная и относительная погрешности

В процессе вычислений весьма часто приходится иметь дело с приближенными числами. Пусть А — точное значение некоторой величины, называемое в дальнейшем точным числом А. Под приближенным значением величины А, или приближенным числам, называется число а, заменяющее точное значение величины А. Если а < А, то а называется приближенным значением числа А по недостатку. Если а > А, — то по избытку. Например, 3,14 является приближенным значением числа π по недостатку, а 3,15 — по избытку. Для характеристики степени точности данного приближения пользуются понятием погрешности или ошибки.

Погрешностью Δа приближенного числа а называется разность вида

Δа = А — а, (1.1)

где А — соответствующее точное число.

Определение. Абсолютной погрешностью А приближенного числа а называется абсолютная величина погрешности этого числа

Δ = |А — а|. (1.2)

В силу того, что точное число А, как правило, неизвестно, то пользуются понятием предельной абсолютной погрешности.

Определение. Предельной абсолютной погрешностью Δ_a приближенного числа а называется число, не меньшее абсолютной погрешности этого числа, т. е.

Δ_a ≥ Δ. (1.3)

Из (1.3) имеем

Δ_a ≥ |А — а|,

следовательно,

а - Δ_a  А  а + Δ_a, (1.4)

т. е. а - Δ_a является приближением числа А по недостатку, а а + Δ_a — приближением числа А по избытку. Формулу (1.4) кратко записывают в виде А = а ± Δ_a.

На практике под точностью измерений обычно понимают предельную абсолютную погрешность. Например, если расстояние между двумя пунктами, равное S = 900 м, получено с точностью до 0,5 м, то точное значение величины S заключено в границах 899,5 м  S  900,5 м.

Введение абсолютной или предельной абсолютной погрешностей совершенно недостаточно для характеристики степени точности приближенных чисел. Существенным показателем точности приближенных чисел является их относительная погрешность.

Определение. Относительной погрешностью δ приближенного числа а называется отношение абсолютной погрешности Δ этого числа к модулю соответствующего точного числа А (А  0)

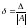. (1.5)

Определение. Предельной относительной погрешностью приближенного числа а называется число δ_а не меньшее относительной погрешности этого числа, т. е.

δ_а ≥ δ. (1.6)

Из (1.6) имеем Δ  |А|δ_а

Следовательно, можно считать, что предельная абсолютная погрешность числа а равна

Δ_а  |А|δ_а. (1.7)

Если принять А  а, то формула (1.7) примет вид

Δ_а  |а|δ_а. (1.8)

Следовательно, точное число А лежит в следующих границах:

а(1 - δ_а)  А  а(1 + δ_а).

Формула (1.8) позволяет определять предельную абсолютную погрешность по заданной предельной относительной погрешности и наоборот.

2. Верные и значащие цифры. Запись приближенных значений

Определение. Значащей цифрой приближенного числа называются всякая цифра в его десятичном изображении, отличная от нуля, и нуль, если он содержится между значащими цифрами или является представителем сохраненного десятичного разряда. Все остальные нули, входящие в состав приближенного числа и служащие лишь для обозначения десятичных разрядов его, не причисляются к значащим цифрам.

Например, в числе 0,002080 первые три нуля не являются значащими цифрами, так как они служат только для установления десятичных разрядов других цифр. Остальные два нуля являются значащими цифрами, так как первый из них находится между значащими цифрами 2 и 8, а второй, как это отражено в записи, указывает, что в приближенном числе сохранен десятичный разряд 10^-6. В случае, если в данном числе 0,002080 последняя цифра не является значащей, то это число должно быть записано в виде 0,00208. С этой точки зрения числа 0,002080 и 0,00208 не равноценны, так как первое из них содержит четыре значащих цифры, а второе — лишь три значащих цифры.

При написании больших чисел нули справа могут служить как для обозначения значащих цифр, так и для определения разрядов остальных цифр. Поэтому при обычной записи чисел могут возникнуть неясности. Например, рассматривая число 689000, мы не имеем возможности по его виду судить о том, сколько в нем значащих цифр. Хотя можно утверждать, что их не меньше трех. Этой неопределенности можно избежать, выявив десятичный порядок числа и записав его в виде 6,89 10⁵, если оно имеет три значащих цифры или 6,8900 10⁵, если число имеет пять значащих цифр, и т. п. Вообще, такого рода запись удобна для чисел, содержащих большое количество незначащих нулей, например 0,000000120 = 1,20 10^-7 и т. п.

Первые п значащих цифр приближенного числа называются верными, если абсолютная погрешность этого числа не больше половины единицы разряда, выражаемого n-й значащей цифрой.

Например, для точного числа А = 14,298 число а = 14,300 является приближенным числом с четырьмя верными знаками, так как

Δ = |А — а | = 0,002 < 0, 5* 0,01 = 0,005.

В процессе вычислений часто происходит округление чисел, т.е. замена чисел их значениями с меньшим количеством значащих цифр. При округлении возникает погрешность, называемая погрешностью округления. Пусть х - данное число, а х₁ - результат округления. Погрешность округления определяется как модуль разности прежнего и нового значений числа:

В отдельных случаях вместо ∆_окр приходится использовать его верхнюю оценку.