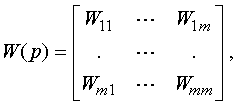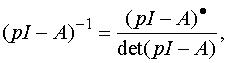9

Министерство образования и науки России

Севастопольский государственный университет

МАТРИЧНЫЕ ОПЕРАЦИИ

С ДИНАМИЧЕСКОЙ СИСТЕМОЙ

Методические указания

к выполнению лабораторной работы по дисциплине

«Математические основы теории систем»

для студентов дневной и заочной форм обучения

направления подготовки

27.03.04 – Управление в технических системах

Севастополь

2014

УДК 681.5

Матричные операции в динамической системе: Методические указания к выполнению лабораторной работы по дисциплине «Математические основы теории систем» для студентов дневной и заочной форм обучения по направлению подготовки 27.03.04 – Управление в технических системах / Сост. А.И.Грушун, Т.А.Грушун.- Севастополь: Изд-во СевГУ, 2014.- 9с.

В методических указаниях рассматриваются вопросы представления и анализа линейных динамических систем, заданных в векторно-матричной форме.

Методические указания предназначены для студентов дневной и заочной форм обучения направления подготовки 27.03.04 – Управление в технических системах .

Методические указания рассмотрены и утверждены на заседании кафедры технической кибернетики СевГУ, протокол №1 от 27 сентября 2014 г.

Допущено учебно-методическим центром СевГУ в качестве методических указаний.

Рецензент: Кожаев Е.А., канд. техн. наук, доцент, доцент кафедры кибернетики и

вычислительной техники СевГУ.

Содержание

1.	Цель работы	3
2.	Краткие теоретические сведения	3
3.	Описание технических и программных средств выполнения работы	6
4.	Порядок выполнения теоретических расчетов	6
5.	Порядок выполнения экспериментальных исследований	6
6.	Содержание отчета о выполнении лабораторной работы	9
7.	Контрольные вопросы	9
	Библиографический список	9

1. Цель работы

Изучение способов и приобретение навыков построения передаточной матрицы линейной динамической системы, а также исследования устойчивости такой системы.

2. Краткие теоретические сведения

Наиболее часто в качестве математической модели динамической системы используются обыкновенные дифференциальные уравнения, которые могут быть записаны в различной форме [1, 2].

В зависимости от числа входных и выходных переменных выделяют [2]:

- одноканальные системы - системы, в которых есть только одна выходная переменная;

- многоканальные (многосвязные, многомерные, взаимосвязные) системы - системы, в которых число выходных переменных больше единицы.

Линейные многоканальные динамические системы обычно описывают системой дифференциальных уравнений первого порядка, представленной в векторно-матричном виде:

.

(2.1)

Здесь - вектор состояния, n - порядок объекта; - вектор управляющих воздействий, ; A – матрица состояний (квадратная матрица коэффициентов); B - прямоугольная матрица коэффициентов. Уравнения (2.1) называются дифференциальными уравнениями состояния.

Выходные переменные системы изменяются в соответствии с уравнением выхода

y = Cx

(2.2)

где - вектор выхода; C - прямоугольная матрица коэффициентов.

Уравнения (2.1) и (2.2) описывают линейную стационарную систему. Если ее параметры меняются с течением времени, то такая динамическая система называется нестационарной, а математическая модель имеет вид (2.1)-(2.2), где элементы матриц являются функциями времени: A=A(t); B=B(t); C=C(t).

Наряду с дифференциальными уравнениями также используются различные их преобразования. Для линейных систем эти уравнения удобнее записывать в символической форме с использованием так называемого оператора дифференцирования

,

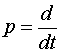что позволяет преобразовывать дифференциальные уравнения как алгебраические и ввести новую динамическую характеристику - передаточную функцию.

Рассмотрим этот переход для многоканальных систем вида

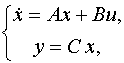
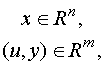
(2.3)

Запишем уравнение состояния в символической форме:

px = Ax + Bu ,

что позволяет определить вектор состояния

(2.4)

и выходные переменные системы

(2.5)

Матрица взаимосвязи между выходными переменными и управляющими воздействиями в выражении (2.5) при нулевых начальных условиях называется матричной передаточной функцией и обозначается (2.6)

(2.6)

Она представляет собой матрицу со следующими компонентами:

(2.7)

где - скалярные передаточные функции, которые представляют собой отношение выходной величины к входной в символической форме при нулевых начальных условиях

Собственными передаточными функциями i-го канала называются компоненты передаточной матрицы , которые находятся на главной диагонали. Составляющие, расположенные выше или ниже главной диагонали, называются передаточными функциями перекрестных связей между каналами.

Обратная матрица находится по выражению

(2.8)

где - присоединенная матрица. Как следует из (2.8), все скалярные передаточные функции, которые являются элементами передаточной матрицы (2.7), содержат одинаковый знаменатель - det(pI-A). Он называется характеристическим полиномом и имеет n-ый порядок.

Если теперь характеристический полином приравнять нулю, то получим характеристическое уравнение системы,

A(p) = det(pI-A) = 0.

(2.9)

Вычислив корни уравнения (2.9) (собственные числа матрицы А) можно определить устойчивость исследуемой динамической системы. Линейная стационарная система устойчива, если все корни ее характеристического уравнения имеют отрицательную действительную часть.

Для примера определим передаточную матрицу для динамической системы

где

Воспользуемся выражением (2.6) для передаточной матрицы (2.7) и найдем предварительно обратную матрицу (2.8). Здесь

Присоединенная матрица имеет вид

,

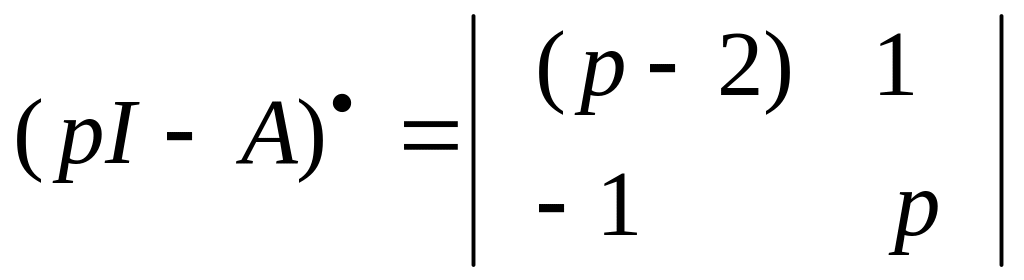a det(pI-A) = p² -2p+1, .

В результате получим следующую обратную матрицу:

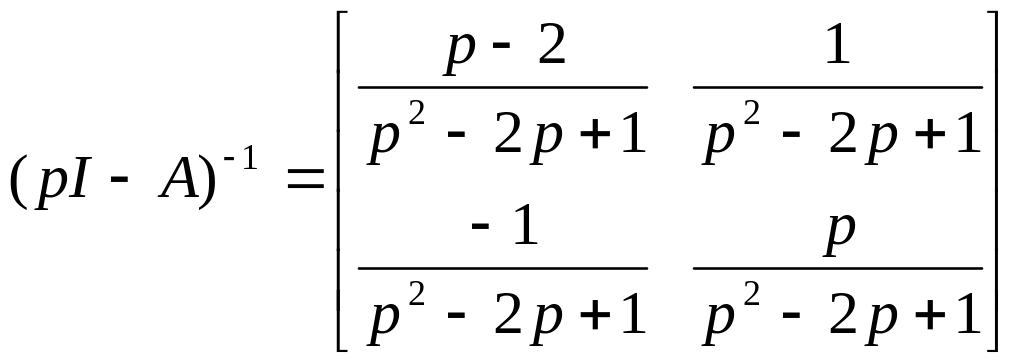
и передаточную матрицу исследуемой системы

.
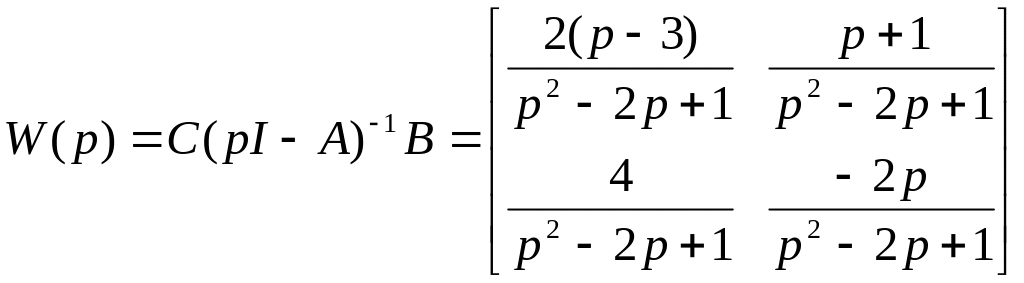