Глава 12

БИОМЕТРИКО-ГЕНЕТИЧЕСКИЙ АНАЛИЗ КАЧЕСТВЕННЫХ ПРИЗНАКОВ

12.1. Общие сведения

Как отмечалось в главе 4 различия между качественными и количественными признаками часто является условным. Кроме того, в селекционно-генетических исследованиях возникает необходимость анализировать количественные и качественные признаки совместно. Причем далеко не всегда точно известна генетическая основа качественной изменчивости признаков. Поэтому, в дополнение к популяционно-генетическому анализу (главы 1-3) разработаны специальные биометрические методы исследования качественных признаков.

Примерами качественной изменчивости могут служить наличие или отсутствие остей колоса у зерновых культур, окраска плода (красная, розовая, желтая, белая) у томатов; наличие или отсутствие заболевания или повреждения растений и т.д. При этом все изучаемые растения по проявлению признака подразделяют на несколько групп. Частным случаем изменчивости, при котором все генотипы объединяют в две группы, является альтернативная изменчивость (наличие или отсутствие шипов на плодах огурца и т.д.).

Существуют общие биометрические задачи изучения изменчивости качественных признаков (П.Ф. Рокицкий): нахождение наиболее типичного значения признака, установление степени вариации вокруг него и зависимости между качественными признаками, достоверности оценки всех полученных показателей.

При изучении качественной изменчивости в селекционно-генетических исследованиях растений могут возникать различные задачи:

- для подбора исходного материала наибольший интерес представляет статистическая проверка данных о наследовании конкретных качественных признаков, в частности, по расщеплению в гибридных поколениях;

- для отбора в популяциях необходимы сведения о связях между качественными признаками, а также между количественными и качественными;

- при выборе лучших генотипов необходимо изучение силы влияния генотипа и факторов среды на изменчивость качественных признаков;

- в нерасщепляющихся поколениях при оценке константного материала по качественным признакам описывают степень гетерогенности сортов, например, в семеноводстве.

12.2. Биометрический анализ изменчивости качественных признаков

Показатели изменчивости. Основные показатели, характеризующие изменчивость качественных признаков и применяющиеся в биометрико-генетических методах:

1. Доля признака в выборке — р₁, р₂,…p_k. Выборочная доля р_i — это относительная численность генотипов с определенным качественным выражением признака в выборке из изучаемой популяции

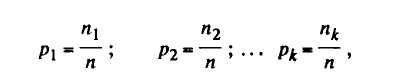
где п — общее число генотипов выборки; п₁, n₂,…п_k — число генотипов, обладающих различными качественными выражениями признака; k — число фенотипических классов или градаций (баллов) признака.

При альтернативной изменчивости долю особей, имеющих определенный признак, обозначают через р, а долю особей без него — через q. Выборочные доли выражают в частях единицы или в процентах.

2. Показатель s характеризует изменчивость качественного признака:

При альтернативной изменчивости формула упрощается:

3. Коэффициент варьирования качественного признака — это отношение показателя изменчивости (s) к максимально возможному его значению при заданном k:

V_p=s/s_max.

При двух градациях признака s_макс=0,5, при трех — 0,33 и т.д.

4. Ошибка выборочной доли характеризует случайные отклонения доли признака в выборке объема п относительно генеральной совокупности (изучаемая популяция, из которой получена выборка)

Ошибка в равной степени относится к любой из выборочных долей совокупности. Приведенную формулу расчета ошибки выборочной доли используют в том случае, если объем выборки очень мал по сравнению с объемом генеральной совокупности. Если объем выборки приближается к объему изучаемой популяции, то в формуле ошибки дается поправка

где N — объем популяции.

5. Доверительный интервал для выборочной доли (р±ts_p) характеризует (с определенным уровнем значимости) возможные границы, в пределах которых находится истинное значение доли в генеральной совокупности. Значения t-критерия Стьюдента при уровне значимости 0,05 или 0,01 берут из приложения 2 для числа степеней свободы п-1.

Пример. Среди изученных 100 растений популяции томата 30 растений оказались штамбовыми, а 70 — обыкновенными. Установить основные параметры изменчивости качественного признака:

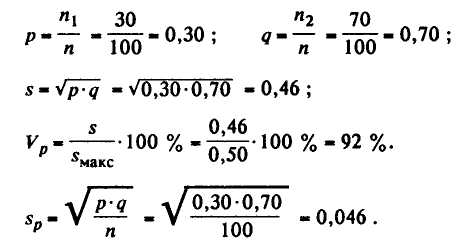
Пределы, в которых с вероятностью 95% лежат истинные значения частоты в популяции:

Следует отметить, что формулу р±ts_p целесообразно применять в том случае, если 0,20<р<0,80. Если же выборочная доля р близка к единице или нулю, то оценка ошибки (s_p) искажена вплоть до вхождения в доверительный интервал доли значений р>1 или р<0.

В этом случае используют функцию преобразования . Ее значение для выборочного p определяют из специальной таблицы, имеющейся в любом справочнике по математической статистике. Стандартная ошибка этого табличного значения: . Далее находят доверительный интервал для , например, при 5%-м уровне значимости: , после чего от максимального и минимального значений  снова, с помощью той же таблицы, возвращаются к границам доверительного интервала для р. Полученные «плечи» доверительного интервал для р уже не будут симметричными.

Оценка достоверности разницы между долями. Достоверность разницы оценивается при сравнении долей по двум качественным признакам в пределах одной выборочной совокупности или по качественному признаку в разных выборках из генеральной совокупности.

В первом случае используют формулу:

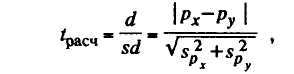
где р_х, р_у — выборочные доли признаков х и у в случайной выборке из п генотипов; — соответствующие ошибки долей признаков х и у.

Пример. Изучены 300 клубней картофеля. 75 из них поражены фитофторой и 100 паршой. Определить достоверность различий по заболеваемости картофеля болезнями:

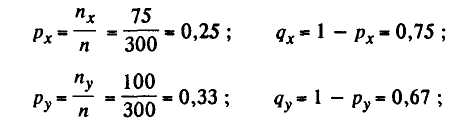
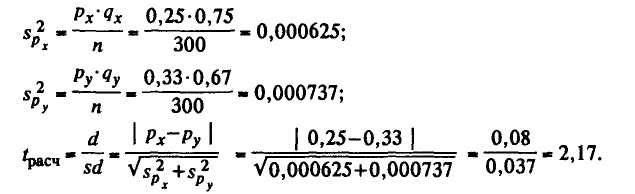
По таблице вероятностей при нормальном распределении (см. приложение 1) находим, что различия долей достоверны, так как при t=2,17 уровень значимости Р=1-0,97 =0,03<0,05.

Если сравнивают выборочные доли по одному качественному признаку из двух выборок, возможно отличающихся по объему (п_хп'_х), то можно применять формулу (П.Ф.Рокицкий):

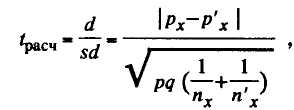
где

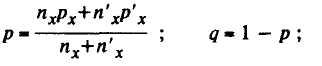
здесь р_х, р'_х — доли особей по признаку х в выборках объемом п_х и п'_х соответственно; р — средняя взвешенная доля; t — критерий Стьюдента.

Последние формулы используют при большом объеме изучаемых выборок, когда t-распределение близко к нормальному.

Пример. Изучены 200 плодов огурца сорта Должик и 300 плодов сорта Нежинский по устойчивости к антракнозу. В сорте Должик выявлены 80 больных плодов, в Нежинском — 90. Проверить нулевую гипотезу об отсутствии различия между сортами по устойчивости к антракнозу:

Уровень значимости Р=0,02<0,5. Нулевая гипотеза отклоняется: различия между сортами по заболеваемости достоверны.