Тема 7: Аналитические методы оптимизации

Экстремальные задачи и методы их решения

Постановка задачи поиска минимума функций содержит:

- целевую функцию > где , определенную на n-мерном евклидовом пространстве . Ее значения характеризуют степень достижения цели, во имя которой поставлена или решается задача;

- множество допустимых решений , среди элементов которого осуществляется поиск.

Требуется найти такой вектор из множества допустимых решений, которому соответствует минимальное значение целевой функции на этом множе­стве:

. (1.1)

1. Задача поиска максимума функции f(x) сводится к задаче поиска ми­нимума путем замены знака перед функцией на противоположный (рис. 7.1):

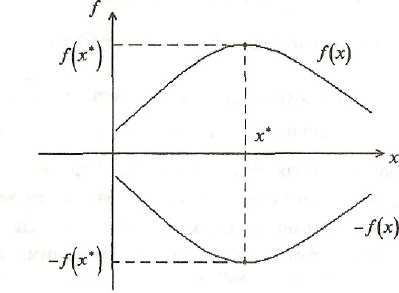
Рис. 7.1

2. Задача поиска минимума и максимума целевой функции f(x) называется задачей поиска экстремума:

3. Если множество допустимых решений X задается ограничениями (условиями), накладываемыми на вектор х , то решается задача поиска условного экстремума. Если , т.е. ограничения (условия) на вектор х отсутствуют, решается задача поиска безусловного экстремума.

4. Решением задачи поиска экстремума является пара , вклю­чающая точку х* и значение целевой функции в ней.

5. Множество точек минимума (максимума) целевой функции f(x) на множестве X обозначим X*. Оно может содержать конечное число точек (в том числе одну), бесконечное число точек или быть пустым.

Определение 1.1. Точка называется точкой глобального (абсолютного) минимума функции f(x) на множестве X, если функция достигает в этой точке своего наименьшего значения, т.е.

.

Определение 1.2. Точка называется точкой локального (относительного) минимума функции f(x) на множестве X, если существует , такое, что если и , то . Здесь - евклидова норма вектора х.

В определении 1.1 точка х* сравнивается со всеми точками из множества допустимых решений X, а в определении 1.2 - только с принадлежащими - окрестности (рис.7.2).

Рис. 7.2

1. Если в определениях 1.1 и 1.2 знак неравенства 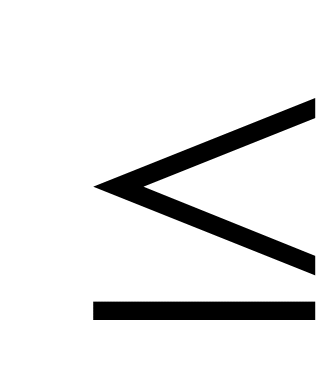заменить на 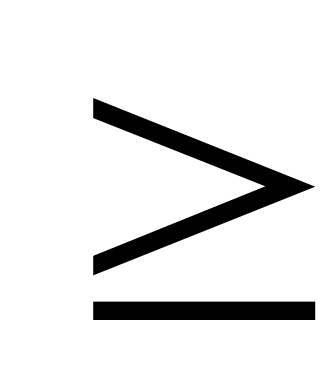>, то получатся определения глобального (абсолютного) и локального (относительного) максимумов.

2. Глобальный экстремум всегда является одновременно локальным, но не наоборот.

Определение 1.3. Поверхностью уровня функции f(x) называется множество точек, в которых функция принимает постоянное значение, т.е. f(х) = const. Если п = 2, поверхность уровня изображается линией уровня на плоскости R².

Пример 1. Найти точки экстремума функции f(x) = \ на множестве .

□Решается задача поиска условного экстремума. Линии уровня функции f(х) представляются окружностями, а множество Х- гиперболой. Имеются две точки глобального минимума:

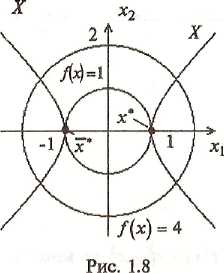
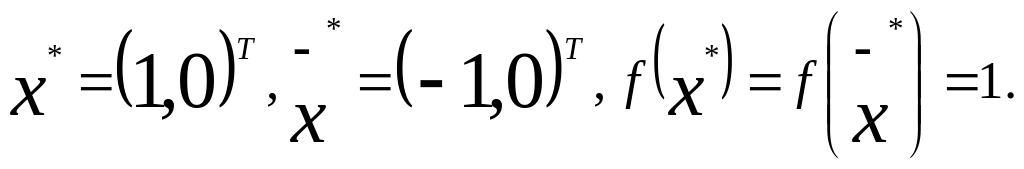
В них выполняется свойство касания линий уровня и кривых, описывающих множество X. Точки глобального и локального максимума отсутствуют. ■

Рис.7.3

Экстремальные свойства выпуклых функций

1. Еслиf(x) выпуклая функция на выпуклом множестве X, то всякая точка локального минимума является точкой ее глобального минимума на X.

2. Если выпуклая функция достигает своего минимума в двух различных точках, то она достигает минимума во всех точках отрезка, соединяющего эти две точки.

2. Если f(x) строго выпуклая функция на выпуклом множестве X, то она может достигать своего глобального минимума на X не более чем в одной точке.

Определение 1.4. Функция f(x) удовлетворяет условию Липшица на отрезке [а, в], если существует такое число L > 0 (константа Липшица), что

(1.3)

для всех х' и х", принадлежащих [а,в] .

Замечания 1.5.

1. Если неравенство (1.3) выполняется с константой L, то оно справедливо для бесконечного множества констант, больших L. Как правило, представляет интерес минимальная из констант Липшица.

1. Из условия (1.3) следует непрерывность функции f(x) на отрезке [а,в]. Если кроме того функция имеет на [а,в] непрерывную производную, то константа Липшица

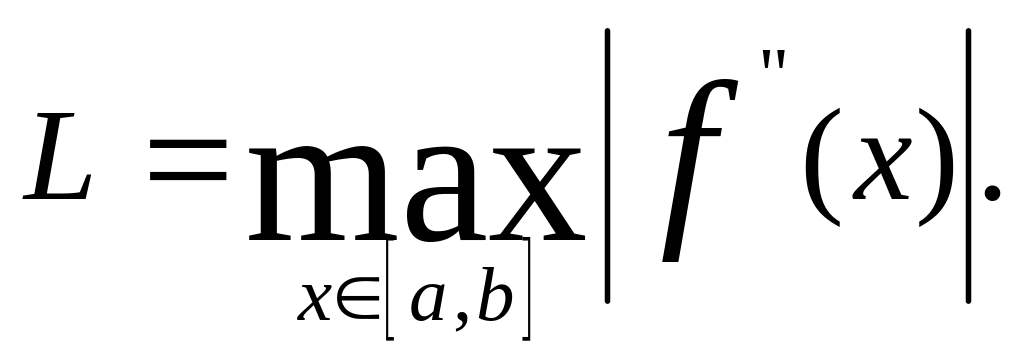
3. Условие (1.3) означает, что модуль углового коэффициента любой хорды графика функции f(х) не превосходит L.

Пример 1.2. Проверить, удовлетворяют ли условию Липшица следующие функции: а) f{x) = 2х на отрезке [0,1]; б) f(x) = sin х на отрезке [0, π]; в) f(x) = на отрезке [0,1].

□ Воспользуемся определением 1.4 и п.2 замечаний 1.5:

а) функция f(x) = 2x удовлетворяет условию Липшица на отрезке [0,1] с константой L = 2;

б) функция f(x) = sin x удовлетворяет условию Липшица на отрезке [0, π] с константой

в) функция f(x) = не удовлетворяет условию Липшица на отрезке [0,1], так как при х→+ 0 угловой коэффициент касательной к графику неограниченно возрастает, а переходя в (1.3) к пределу при | х - х" | → 0, можно заключить, что если в некоторой точке существует касательная к графику функции f{x) , то модуль ее углового коэффициента не может превышать L. ■