- •Identificarea modurilor de căutare simplă a soluțiilor în spațiile stărilor problemelor;
- •Finalitățile lecției
- •Algorimul greedy (cel-mai-bun-întîi - best-first-search)
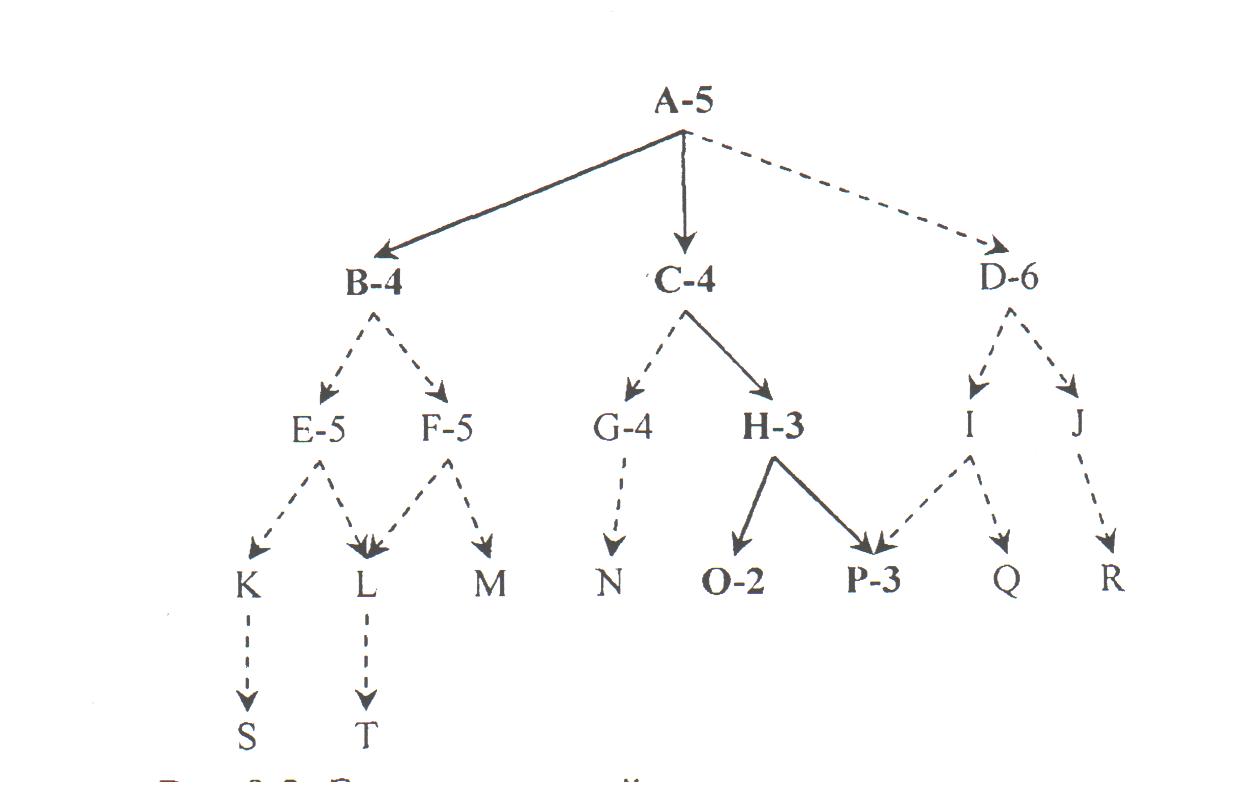
- •Fig. 3.1. Vizitarea nodurilor arborelui cu ajutorul algoritmului greedy
- •Inițial a fost luat nodul a-5
- •Algoritmul a*
- •Fig. 3.2. Găsirea soluției cu ajutorul algoritmului a*
- •Procedura minimax pe grafuri.
- •Fig. 3.3. Spațiul stărilor pentru jocul nim cu 7 fișe
LECȚIA 3- METODE EURISTICE DE CĂUTARE ÎN SPAȚIUL STĂRILOR. |
PETIC M., 2014 |
Competențe prealabile:
Posedarea la nivel teoretic și aplicativ a cunoștințelor despre tablouri uni și bidimensionale, arbori și grafuri;
Posedarea deprindelor de lucru cu MS OFFICE: elaborare de documente WORD, prezentări Power Point etc;
Programarea în limbaje imperative a algoritmilor clasici;
Navigarea pe Internet. Căutare de informații folosind motoare de căutare.
Competențe dezvoltate în cadrul lecției 2:
Identificarea modurilor de căutare simplă a soluțiilor în spațiile stărilor problemelor;
Stabilirea tehnicii computaționale necesare pentru rezolvarea unei probleme căutare a soluției în spațiul stărilor;
Clasificarea modurilor de căutare simplă a soluțiilor în sisteme inteligente.
Finalitățile lecției
Studentul va fi capabil:
Să explice noțiunea de spațiul stărilor
Să clasifice tipurile de căutare euristică a soluțiilor în sisteme inteligente
Să dea exemple de reprezentare a spațiilor stărilor a problemelor inteligente
Metodele de căutare euristică se bazează pe aprecierea valorii unei stări ori a distanței la care se află ea față de o stare finală. Anumite euristici (generate de existența unor cunostințe asupra problemei) pot, în anumite cazuri, reduce efortul de căutare, dar, în acelasi timp, metodele de acest tip nu mai garantează găsirea căii minime care era garantată la căutarea în lățime. Interesul este de a reduce atît dimensiunea soluției (ca lungime a ei sau cost), cît și efortul de căutare pentru găsirea unei soluții. În cele ce urmează, pentru că spațiul stărilor este organizat ca arbore sau graf, stările vor fi asociate nodurilor acestor structuri.
Aceste metode de căutare pot fi folosite atunci cînd e posibil de a deduce careva reguli empirice, care permit micșorarea volumului de variante ce trebuie verificate. Informația empirică se bazează pe experiență, logică și intuiție.
În acest caz a fost introdusă noțiunea de funcție de evaluare f(n), care stabilește costul drumului cel mai scurt din nodul inițial în nodul țintă cu condiția că el va trece prin nodul n. Astfel pentru a alege un nod pentru trecere, se ia cel care are valoarea funcției de evaluare cea mai mică.
Vom nota f(n)=h(n), unde h(n) reprezintă costul euristic a distanței de la starea n către scopul final. De exemplu în jocul perspico pentru situația:
2 |
8 |
3 |
|
1 |
2 |
3 |
1 |
|
4 |
=== |
8 |
|
4 |
7 |
6 |
5 |
|
7 |
6 |
5 |
h(n)=3.
Algorimul greedy (cel-mai-bun-întîi - best-first-search)
Dintr-un anumit punct de vedere, metoda de căutare cel-mai-bun-întîi (best-first search) poate fi considerată o combinare a metodelor de căutare în lățime și lungime. Ca si primele două și aici avem o structură care memorează nodurile ce urmează a fi vizitate. Spre deosebire însă de metodele menționate, în cazul metodei cel-mai-bun-întîi trebuie făcută o apreciere a unui nod, printr-un scor atasat lui, ce caracterizează “distanța” pînă la un nod final, sau dificultatea de a atinge soluția.
Astfel văzut, un scor mic caracterizează o stare apropiată de final, iar un scor mare – una depărtată. La fiecare pas lista se sortează în ordinea crescătoare a scorurilor nodurilor ei, ceea ce permite să se aleagă pentru explorarea ce urmează cel mai promițător (mai aproape de soluție, sau mai usor de atins) nod dintre cele ce se învecinează cu nodurile deja vizitate. Ca și în cazul primelor două metode, metoda poate fi aplicată în egală măsură parcurgerii arborilor ori grafurilor.
În felul acesta algoritmul GREEDY în baza unei careva evaluări euristice la fiecare pas se verifică stările cele mai bune.