1.3.2. Угловая модуляция

При угловой модуляции по закону управляющего колебания изменяется частота или фаза несущего, а амплитуда остается неизменной.

Для гармонического колебания s(t) = S_mSin(₀t + ₀) = S_mSin(t) набег фазы за какой-либо конечный промежуток времени от t=t₁ до

Рис.3. Осциллограмма однотонального АМ колебания при М = 1

t=t₂ равен (t₂) - (t₁) = (₀t₂ + ₀) - (₀t₁+₀) = ₀(t₂ - t₁). При постоянной угловой частоте набег фазы за какой-либо промежуток времени пропорционален длительности этого промежутка.

Угловую частоту можно определить как ₀=( [t₂]-[t₁])/{t₂-t₁}, то есть угловая частота – это скорость изменения фазы колебания.

Переходя к сложному колебанию, частота которого может изменяться во времени необходимо перейти к дифференциальным и интегральным соотношениям:

	(7)
	(8)

Из (7), (8) следует, что полная фаза высокочастотного колебания в момент t:

(9)

Итак, в общем виде выражение для высокочастотного колебания, амплитуда которого постоянна, а аргумент (t) модулирован:

(10)

Соотношения (8), (9), устанавливающие связь между изменениями частоты и фазы, указывают на общность двух разновидностей угловой модуляции. Рассмотрим пример простейшей гармонической ЧМ, когда мгновенная частота определяется как:

(11)

где _Д = 2f_Д – амплитуда частотного отклонения или девиация частоты (или просто девиация); ₀ – несущая,  – модулирующая частоты.

Подставим (11) в (9):

.

(12)

Проинтегрировав, подставим в (10):

(13)

Полученное модулированное колебание можно рассматривать и как модулированное по фазе, закон этой модуляции является интегральным по отношению к закону изменения частоты.

Таким образом, модуляция частоты несущего колебания по закону _ДCost приводит к модуляции фазы по закону (_Д/)Sint. Амплитуду изменения фазы называют индексом угловой модуляции (14):

(14)

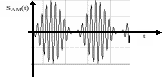
Пример осциллограммы с однотональной ЧМ приведен на рис. 4.

Рис.4. Осциллограмма однотонального ЧМ колебания

2. Прохождение детерминированных сигналов через линейные стационарные цепи с сосредоточенными параметрами

Любое радиотехническое устройство представляет собой систему, то есть совокупность физических объектов, между которыми существуют определенные взаимодействия.

В системе можно выделить вход, на который подается исходный сигнал, и выход, откуда снимается преобразованный сигнал.

Если интересует только связь между входными и выходными сигналами и не рассматривают внутренние процессы в системе, то систему рассматривают как «черный ящик» (рис. 5).

Рис.5. Система как «черный ящик»

Закон связи между входным сигналом U_вх(t) и выходным сигналом (откликом, выходной реакцией системы) U_вых(t) задается системным оператором Т:

(15)

При исследовании необходимо указывать область допустимых входных и выходных воздействий, которые описывают характер сигналов (непрерывных, дискретных, детерминированных, случайных и т. д.).

Математической моделью (ММ) системы называют совокупность системного оператора Т и областей допустимых сигналов.

На основании свойств ММ можно проводить классификацию систем.
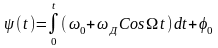