Передавальну функцію дискретного фільтра (14) потрібно перетворити до вигляду (8) після чого легко отримати різницеве рівняння для розрахунку вихідного сигналу представлене співвідношенням (7).

Відповідно до описаної методики отримане різницеве рівняння для формування подовжньої складової вітру

(15)

де Тут і далі при формуванні поривів вітру вхідна випадкова послідовність чисел нормальна з параметрами (0, 1).

Описана методика розрахунку коефіцієнтів різницевого рівняння (12) може бути модифікована, якщо врахувати справедливість рівняння

(16)

Оскільки , то з (16) слідує рівність

Переходячи до кінцево-різницевого представлення похідної у вигляді

отримаємо різницеве рівняння для k-тої складової вихідного сигналу

(17)

де , .

Дискретна передавальна функція в цьому випадку представляється співвідношенням

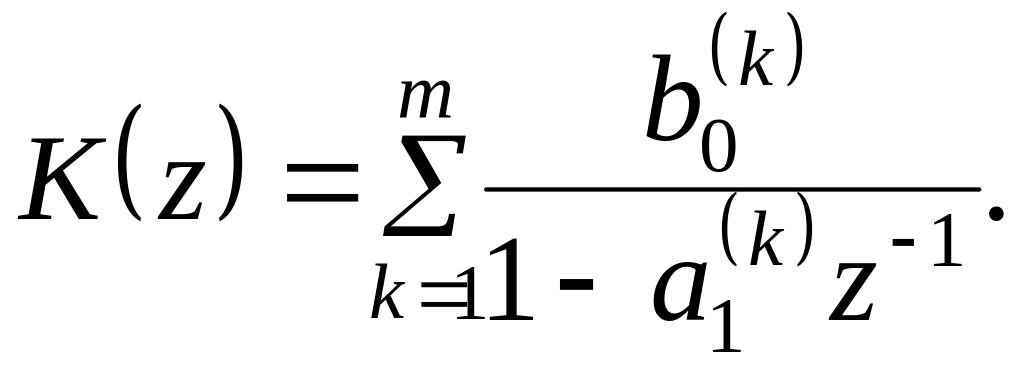(18)

Різницеве рівняння для формування подовжньої складової випадкових поривів вітру буде

(19)

де

Побудова різницевого рівняння для моделювання поперечної складової вітру відповідно до цієї методики неможлива, оскільки передавальна функція K_n(р) має один кратний полюс. У цьому випадку застосуємо спосіб отримання дискретної передавальної функції формуючого фільтра шляхом представлення передавальної функції по Лапласу у вигляді відношення лінійних комбінацій інтегруючих ланок різного порядку. Для цього її чисельник і знаменник ділять на p^m, де m порядок передавальної функції. Після цього проводиться заміна операторів інтегрування 1/p^l (m l) їх дискретними аналогами. Останні можуть мати різне представлення в залежності від способу інтегрування. Приведемо для довідки табл. 2, взяту з книги Леонова, для двох способів інтегрування.

Із застосуванням приведених довідкових даних отримані дискретні передавальні функції і відповідні їм різницеві рівняння для формування подовжньої і поперечної складових вітру. Так для подовжньої складової у разі представлення оператора інтегрування його z-перетворенням з інтегратором нульового порядку алгоритм формування повністю співпадає з (19), а при використанні інтегратора першого порядку представляється рівнянням вигляду (15). Коефіцієнти рівняння (15) в цьому випадку визначаються співвідношеннями

Таблиця 2 - Приклади z-перетворень операторів інтегрування

Оператор безперервного інтегрування	z-перетворення оператора інтегрування з інтегратором
	нульового порядку	першого порядку

Для отримання різницевого рівняння формування складових поперечного вітру заздалегідь представимо передавальну функцію K_n(p) у вигляді

(20)

де

Якщо використати z-перетворення з інтегратором нульового порядку отримаємо різницеве рівняння

(21)

де

Застосування z-перетворення з інтегратором першого порядку приводить до різницевого рівняння

(22)

Коефіцієнти цього рівняння при введенні позначення представляються у вигляді

Моделювання показало, що в деяких випадках різницеве рівняння з прийнятною для моделювання випадкового процесу точністю може бути отримане безпосередньо з передавальної функції по Лапласу. Для цього від передавальної функції слід, вважаючи початкові умови нульовими, перейти до зображувального рівняння. Наприклад, для передавальної функції (20) воно має вигляд

Замінивши оператори диференціювання їх кінцево-різницевими наближеннями, наприклад,

(23)

після перетворень отримаємо кінцево-різницеве рівняння

(24)

Значення коефіцієнтів останнього рівняння обчислюються по формулах

при

Заміна першої похідної наближенням приводить до рівняння виду (24), в якому коефіцієнти b₀, b₁ мають той самий вигляд, а при

Подібним чином отримане різницеве рівняння для формування подовжньої складової вітру вигляду (19). Тут а

Підстановки вигляду (23) не єдині можливі. Заміна операторів диференціювання операторами кінцево-різницевого диференціювання іншого вигляду приведе до зміни результуючого кінцево-різницевого рівняння.

У всіх випадках необхідно, щоб результуюче кінцево-різницеве рівняння було стійким. Критерієм стійкості ітераційного кінцево-різницевого рівняння є попадання усіх коренів його характеристичного рівняння в одиничне коло на комплексній площині. Характеристичне рівняння для дискретної передавальної функції (8) і відповідного їй різницевого рівняння має вигляд

(25)

Перевірка отриманих вище різницевих рівнянь по вказаному критерію показала їх стійкість. Нестійке різницеве рівняння, що підтверджується як критерієм, так і результатами чисельного експерименту формування складової поперечного вітру, буде отримане, наприклад, при наближеному обчисленні першої похідної по формулі

Якщо порядок характеристичного рівняння вище другого, визначення його коренів може викликати труднощі. У цьому випадку для оцінки стійкості різницевого рівняння доцільно скористатися в (25) заміною .

Внаслідок перетворень буде отримане рівняння того ж порядку, але корені цього рівняння для стійкого різницевого рівняння будуть знаходитись в лівій напівплощині комплексної площини. У цьому випадку перевірка стійкості може проводитись по відомих критеріях, наприклад, по критерію Гурвіца.

П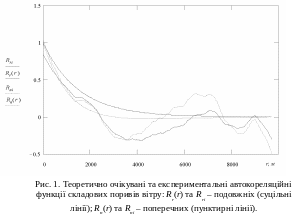 риклади автокореляційних функцій складових подовжньої і поперечної складових вітру за результатами математичного моделювання за різницевими рівняннями (19), (21) у порівнянні з теоретично очікуваними (3) представлені на рис. 1. Пунктирними та суцільними лініями виділені пари

кривих (теоретично очікуваної R(r) та експериментальної R_i) для поперечної та подовжньої складових вітру відповідно. Параметри вітру при моделюванні складали: масштаб турбулентностей L = 1500 м; середньоквадратичне відхилення складових вітру σ_w = 1 м/с. З рисунку видно непогану відповідність теоретичних та експериментальних кривих для значень r < L. Подальші коливання експериментальних кривих є випадковими й при осереднені великої кількості експериментальних кривих результат буде наближатися до теоретично очікуваного.