
- •Передмова.
- •1. Деякі поняття теорії множин.
- •2. Основні числові множини. Дійсні числа. Числова вісь, проміжки на ній. Модуль дійсного числа.
- •3. Аксіоми дійсних чисел.
- •4. Обмежені множини.
- •5. Нескінченні множини. Порівняння нескінченних множин.
- •6. Зліченні множини та їх властивості.
- •7. Потужність континууму.
- •8. Числова послідовність, види послідовностей.
- •9. Границя послідовності.
- •10. Властивості границь послідовностей.
- •11. Нескінченно малі та нескінченно великі послідовності.
- •12. Границя монотонної та обмеженої послідовності. Число . Теорема Кантора про вкладені відрізки.
- •13. Підпослідовності. Часткові границі.
- •14. Критерій Коші збіжності числової послідовності.
- •15. Поняття функції, способи задання функції. Основні елементарні функції та їх графіки.
УДК 517.1
ББК 22.161.
Щ92
Вступ до аналізу.
Автори:
Щоголев С. А., доктор фізико-математических наук, професор кафедри вищої математики, доцент
Грибняк С. Т., кандидат фізико-математичних наук, доцент кафедри вищої математики, доцент
Рецензенти.
Попов В. Г. – доктор фізико-математичних наук,
завідуючий кафедрою вищої математики Одеської національної
морської академії, професор
Плотніков А. В. – доктор фізико-математичних наук,
завідуючий кафедрою прикладної та обчислювальної
математики і САПР Одеської державної академії
будівництва та архітектури, професор
Григор’єв Ю. О. – кандидат фізико-математичних наук,
доцент кафедри вищої та прикладної математики
Одеського національного морського університету, доцент
Навчально-методичний посібник написано відповідно до навчальної програми дисципліни «Математичний аналіз» для підготовки бакалаврів, спеціалістів та магістрів за спеціальностями «фізика», «прикладна фізика», «астрономія».
Посібник містить основні поняття, методи, теореми та формули, багато розв’язаних типових задач, а також завдання для самостійної роботи студентів.
Рекомендовано науково-методичною радою ОНУ імени І. І. Мечникова (протокол № 1 от 24.10.2013).
Передмова.
Даний
посібник є першою складовою частиною
серії посібників авторів з курсу
математичного аналізу, який читається
ними на 1-му та 2-му курсах фізичного
факультету ОНУ для студентів спеціальностей
«фізика», “прикладна фізика”,
«астрономія». Одним з базових понять
математичного аналізу є поняття границі,
на якому ґрунтуються інші важливіші
поняття, зокрема такі, як похідна та
інтеграл. Разом з цим оволодіння цим
поняттям студентами наштовхується на
певні труднощі. Викладення тем “Границя
послідовності” і “Границя функції”
відбувається, як правило, на початку
читання курсу математичного аналізу.
А загальноприйнята мова “ ”
(для послідовностей) і “
”
(для послідовностей) і “ ”
(для функцій) означень цих понять важка
для сприймання вчорашніми школярами,
особливо, якщо врахувати сучасний рівень
підготовки у середніх навчальних
закладах. Цей факт, зокрема, з’явився
причиною того, що в деяких курсах вищої
математики та математичного аналізу
для нематематичних спеціальностей,
навіть для фізичних (наприклад, книга
Я.Б.Зельдовича та І.М.Яглома «Высшая
математика для начинающих физиков и
техников»,
М., 1982) автори взагалі намагалися уникнути
теми “Границя”, і хоча термін “границя”
використовувався при введенні понять
похідної та інтеграла, строгого означення
поняття границі не давалося, і це, на
думку автора, створило певні труднощі
при викладенні подальшого матеріалу.
Положення з темою “Границя” при
викладанні курсу погіршується ще тим,
що внаслідок обмеженої кількості
навчальних годин нема можливості більш
менш детально зупинитися на відповідній
теорії.
”
(для функцій) означень цих понять важка
для сприймання вчорашніми школярами,
особливо, якщо врахувати сучасний рівень
підготовки у середніх навчальних
закладах. Цей факт, зокрема, з’явився
причиною того, що в деяких курсах вищої
математики та математичного аналізу
для нематематичних спеціальностей,
навіть для фізичних (наприклад, книга
Я.Б.Зельдовича та І.М.Яглома «Высшая
математика для начинающих физиков и
техников»,
М., 1982) автори взагалі намагалися уникнути
теми “Границя”, і хоча термін “границя”
використовувався при введенні понять
похідної та інтеграла, строгого означення
поняття границі не давалося, і це, на
думку автора, створило певні труднощі
при викладенні подальшого матеріалу.
Положення з темою “Границя” при
викладанні курсу погіршується ще тим,
що внаслідок обмеженої кількості
навчальних годин нема можливості більш
менш детально зупинитися на відповідній
теорії.
З іншого боку, на думку багатьох фахівців фізиків (зокрема, Л. Д. Ландау) детальне оволодіння строгими математичними означеннями для студентів фізиків навіть необов’язково, достатньо усвідомити ці поняття на інтуїтивному рівні і оволодіти відповідною технікою розв’язування задач.
Але не менш скрутне становище виникає при проведенні практичних занять по темі “Обчислення границь послідовностей та функцій”, тобто на оволодіння цією самою технікою. Існує багато різних методів обчислення границь, розкриття різних типів невизначеностей, але за тими самими причинами вони майже не висвітлюються. Викладачам доводиться обмежуватися правилом Лопіталя.
Даний посібник має своєю метою певною мірою виправити цей недолік. Викладення поняття “границя” проводиться засобом, який декілька відрізняється від загальноприйнятого тим, що означення на мові “ ” і “ ” дається не одразу, а після розглядання низки прикладів, які дозволяють, на думку автора, уяснити поняття границі спочатку на інтуїтивному рівні, і лише потім даються точні означення. Розглянуто також методи розкриття деяких типів невизначеностей, які ілюструються на конкретних прикладах, хоча ці питання можна було б винести цілком на практичні заняття.
1. Деякі поняття теорії множин.
Математика
(від грецького
 – наука,
система знань) – це наука про кількісні
відношення, просторові форми та
логічні структури навколишнього світу.
Як наука математика має певні особливості,
що відрізняють її від інших наук. Зокрема,
об’єктом
дослідження можуть бути абстрактні
форми, незалежно від їх змісту. Математичні
результати отримуються шляхом логічного
висновку з основних понять та тверджень.
Посилання на досвід не є математичним
аргументом. Подальші результати
математики не можуть відмінити попередніх.
Результати математики універсальні –
у будь якій галузі, де вдається поставити
задачу математично, математика дає
результат з точністю, що відповідає
точності початкових даних.
– наука,
система знань) – це наука про кількісні
відношення, просторові форми та
логічні структури навколишнього світу.
Як наука математика має певні особливості,
що відрізняють її від інших наук. Зокрема,
об’єктом
дослідження можуть бути абстрактні
форми, незалежно від їх змісту. Математичні
результати отримуються шляхом логічного
висновку з основних понять та тверджень.
Посилання на досвід не є математичним
аргументом. Подальші результати
математики не можуть відмінити попередніх.
Результати математики універсальні –
у будь якій галузі, де вдається поставити
задачу математично, математика дає
результат з точністю, що відповідає
точності початкових даних.
Однакові математичні моделі можуть описувати зовсім різні процеси та явища. Наприклад, формула
 описує
і закон всесвітнього тяжіння, і закон
Кулона взаємодії між електричними
зарядами. За влучним висловленням
видатного французького математика Анрі
Пуанкаре «математика
– це мистецтво надавати різним речам
одне й те ж найменування».
описує
і закон всесвітнього тяжіння, і закон
Кулона взаємодії між електричними
зарядами. За влучним висловленням
видатного французького математика Анрі
Пуанкаре «математика
– це мистецтво надавати різним речам
одне й те ж найменування».
Сучасна математика являє собою величезну сукупність різних напрямків, значна частина яких є самостійними науками. Однією з найважливіших частин математики є математичний аналіз, поняття, результати і методи якого використовуються практично в усіх природничих науках. Зокрема, ефективне вивчення фізики неможливо без володіння математичним аналізом. Дуже багато понять математичного аналізу мають свою фізичну інтерпретацію. Але це не означає, що математичне поняття можна підміняти його інтерпретацією, інтерпретація не тотожна цьому поняттю – в різних науках ці інтерпретації можуть бути різними, а суто математичне поняття залишається незмінним. Скажемо, похідна функції не є тільки швидкість, як пропонують вважати деякі фізики. Наприклад, з геометричної точки зору та ж сама похідна є кутовим коефіцієнтом дотичної, проведеної до графіка функції. Навіть суто фізичні інтерпретації одного й того ж математичного поняття можуть бути різними, наприклад, одним й тим же визначеним інтегралом Рімана може виражатися і маса тіла, і пройдений шлях, і робота сили і багато інших речей. Тому для ефективного вміння застосовувати математичні поняття та методи необхідно добре розуміти самі ці поняття, а не тільки їх інтерпретацію. Крім того, математика має свою внутрішню логіку, розуміння якої безумовно також необхідно для ефективного використання математичних методів. Тому не можна математику розглядати тільки як технічний апарат розв’язування прикладних задач. І не можна зводити математику взагалі та математичний аналіз зокрема тільки до деякої збірки рецептів і оволодіння певною технікою. Виходячи з цих міркувань ми й викладаємо математичні науки для студентів як фізичних, так і інших спеціальностей.
Під математичним аналізом (або просто аналізом) розуміється сукупність розділів математики, присвячених дослідженню функцій методами так званих нескінченно малих. Цей метод мав своє започаткування ще в стародавні часи (Євдокс, Архімед та ін.), але послідовну теорію було створено лише в XVII–XVIII ст. н.е. у працях І. Ньютона, Г. Лейбніца, а потім Л. Ейлера, К. Гауса, Ж. Лагранжа, О. Коші, К. Вейєрштрасса та ін.
Всі твердження, які зустрічаються в математиці, якщо вони не входять до прийнятої системи аксіом, обов’язково мають бути доведені. В математиці використовуються різні типи доведень.
Пряме доведення. Коли твердження виводиться як логічний наслідок з прийнятих аксіом та вже доведених тверджень.
Доведення
від протилежного.
Нехай при виконанні деякої сукупності
умов нам треба довести твердження
 .
Ми припускаємо, що
– невірне. І далі за допомогою логічних
міркувань ми приходимо до протиріччя
або з прийнятими умовами, або з деякими
фактами, справедливість яких не підлягає
сумніву. Грунтується цей метод на
логічному законі:
.
Ми припускаємо, що
– невірне. І далі за допомогою логічних
міркувань ми приходимо до протиріччя
або з прийнятими умовами, або з деякими
фактами, справедливість яких не підлягає
сумніву. Грунтується цей метод на
логічному законі:
 .
.
Метод
математичної індукції.
Нехай треба довести, що деяке твердження
 справедливе для будь якого натурального
числа
справедливе для будь якого натурального
числа
 .
Спочатку доводиться його справедливість
для
.
Спочатку доводиться його справедливість
для
 ,
тобто доводиться, що
,
тобто доводиться, що
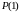 – вірне. Потім припускається, що
справедливе для
– вірне. Потім припускається, що
справедливе для
 ,
тобто
,
тобто
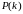 – вірне. І далі на підставі цього
доводиться, що
справедливе для
– вірне. І далі на підставі цього
доводиться, що
справедливе для
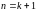 .
Тоді з справедливості
буде випливати справедливість
.
Тоді з справедливості
буде випливати справедливість
 ,
звідси
,
звідси
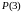 тощо.
тощо.
Як і інші науки, математика ґрунтується на деяких поняттях, які неможливо визначити через інші поняття, і які є початковими. Вважається, що ці поняття можна зрозуміти на інтуїтивному рівні. Одним з таких понять є поняття множини. Під множиною ми розуміємо сукупність деяких об’єктів, взагалі кажучи, довільної природи. Як правило, являють інтерес сукупності таких об’єктів, які поєднуються якою-небудь спільною ознакою, чи властивістю. Наприклад, множина студентів у групі, множина наукових теорій, множина планет у Сонячній системі, множина країн, що входять до СОТ, множина чисел у проміжку (0;1) та ін.
Об’єкти, які складають множину, називаються елементами множини. Якщо цих елементів скінченна кількість, то множина називається скінченною, у протилежному випадку нескінченною. Наприклад, множина карт у гральній колоді скінченна, а множина трикутників, подібних даному – нескінченна.
Домовимось
позначати множини великими буквами
латинського алфавіту:
 а
їх елементи відповідно малими:
а
їх елементи відповідно малими:
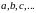 .
Якщо елемент
.
Якщо елемент
 належить множині
належить множині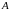 ,
то пишемо:
,
то пишемо:
 .
Якщо не належить, то пишемо:
.
Якщо не належить, то пишемо:
 .
.
Множина,
яка не містить жодного елемента,
називається порожньою
і позначається символом .
Наприклад порожньою множиною є множина
від’ємних
коренів рівняння
.
Наприклад порожньою множиною є множина
від’ємних
коренів рівняння
 .
.
Для запису множини використовуються фігурні дужки, елементи множини відокремлюються комами. Наприклад:
 .
.
Множина
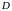 нескінченна. Далі ми покажемо принципову
різницю між скінченними та нескінченними
множинами.
нескінченна. Далі ми покажемо принципову
різницю між скінченними та нескінченними
множинами.
Дві
множини називаються рівними,
якщо вони складаються з одних і тих же
елементів. Наприклад, множина
 і
і
 – рівні (порядок слідкування елементів
не відіграє ролі). Пишемо:
– рівні (порядок слідкування елементів
не відіграє ролі). Пишемо:
 .
.
Множина
![]() називається підмножиною
множини
називається підмножиною
множини
![]() ,
якщо кожен елемент множини
являється елементом множини
.
Пишемо:
,
якщо кожен елемент множини
являється елементом множини
.
Пишемо:
![]() .
Зокрема множина
може співпадати з множиною
.
Тоді пишемо:
.
Зокрема множина
може співпадати з множиною
.
Тоді пишемо:
![]() .
Наприклад, якщо
.
Наприклад, якщо
![]() ,
то
,
,
то
,
![]() .
.
Порожня множина є підмножиною будь якої множини. Дійсно, нехай – довільна множина. Якщо припустити, що не є її підмножиною, то у множині знайдеться принаймні один елемент, який не належить множині . Але тоді вийшло б, що містить принаймні один елемент, що суперечить означенню порожньої множини.
Приклад.
Задано множину
 .
Записати всі підмножини цієї множини.
.
Записати всі підмножини цієї множини.
Маємо:
 .
.
Тобто
всього 8 підмножин. Можна легко показати,
що множина, яка містить
елементів, має
 підмножин, враховуючи саму цю множину
і порожню множину.
підмножин, враховуючи саму цю множину
і порожню множину.
Визначимо деякі операції, які можна виконувати над множинами.
Множину
 ,
яка містить ті та тільки ті елементи,
які належать хоча б одній з множин
і
,
називається об’єднанням
множин
і
,
і позначається:
,
яка містить ті та тільки ті елементи,
які належать хоча б одній з множин
і
,
називається об’єднанням
множин
і
,
і позначається:
 .
.
Множина
,
яка містить ті та тільки ті елементи,
які належать водночас обом множинам
і
,
називається перетином
множин
і
,
і позначається:
 .
.
Приклад.
Нехай
 .
Тоді
.
Тоді
 .
.
Поняття об’єднання і перетину множин наглядно ілюструються геометрично (рис.1):
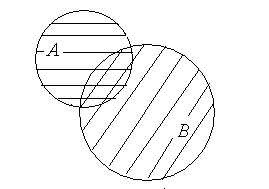
Рис. 1.
Якщо множини і умовно зобразити кругами з різними штриховками на площині, то перетин множин і – це область, де присутні обидві штриховки (спільна частина кругів), а об’єднання цих множин – область, де є хоч би одна штриховка.
Різницею
множин
і
,
назвемо всі елементи множини
,
які не входять до множини
.
Позначається:
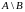 .
Тобто
.
Тобто
 тоді і тільки тоді, коли
,
тоді і тільки тоді, коли
, .
Наприклад, якщо
.
Наприклад, якщо ,
то
,
то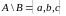 .
На рис.2 наведено геометричну ілюстрацію
цього поняття:
.
На рис.2 наведено геометричну ілюстрацію
цього поняття:
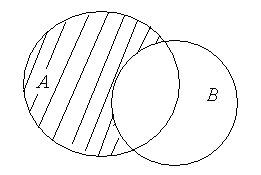
Рис. 2.
Штриховкою показано множину .
Нехай
задано довільну систему множин
Множину
 назвемо універсальною
множиною
для цієї системи, якщо кожна множина
цієї системи являється підмножиною
множини
тобто
назвемо універсальною
множиною
для цієї системи, якщо кожна множина
цієї системи являється підмножиною
множини
тобто

 (рис.3).
(рис.3).
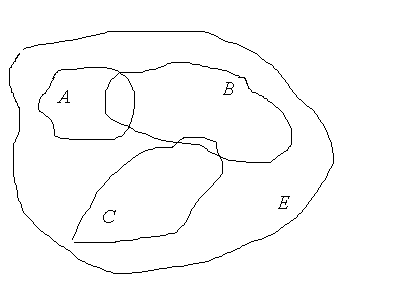
Рис. 3.
Доповненням
множини
до універсальної називається множина
 .
Наприклад, якщо
– множина натуральних чисел,
– множина парних чисел, то
.
Наприклад, якщо
– множина натуральних чисел,
– множина парних чисел, то
 – множина непарних чисел (враховуючи
одиницю). Графічна ілюстрація показана
на рис.4.
– множина непарних чисел (враховуючи
одиницю). Графічна ілюстрація показана
на рис.4.
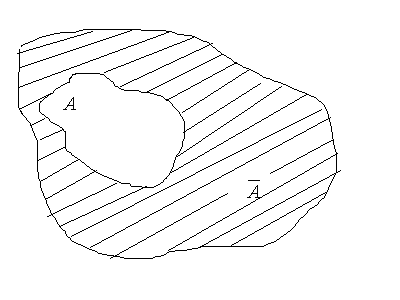
Рис.4.
Визначимо деякі властивості дій над множинами:
1)
 ,
,
2)
 ,
,
3)
 ,
,
4)
 ,
,
5)
 ,
,
6)
 ,
,
7)
 ,
,
8)
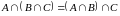 ,
,
9)
 ,
,
10)
 ,
,
11)
 ,
,
12)
 ,
,
13)
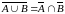 ,
,
14)
 .
.
Дві
останні властивості називаються законами
де Моргана.
Аналоги цих законів є також в алгебрі
висловлювань та теорії ймовірностей.
Доведемо властивість 13). Щоб це зробити,
треба показати, що будь який елемент,
який належить множині
 ,
належить також і
,
належить також і
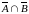 ,
і навпаки, будь який елемент, який
належить
,
належить також і
.
Отже, нехай
,
і навпаки, будь який елемент, який
належить
,
належить також і
.
Отже, нехай
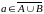 .
Тоді
.
Тоді
 .
Навпаки, нехай
.
Навпаки, нехай
 .
Тоді
.
Тоді

 .
А звідси випливає, що
,
що й треба було довести.
.
А звідси випливає, що
,
що й треба було довести.
Властивість 14) спробуйте довести самостійно.
У подальшому ми часто будемо використовувати слідуючи символи (так звані квантори):
 – квантор
загальності. Означає “для будь якого”,
“для кожного”, “для всіх”. Походить
від англійського слова
Any
–
будь
який (береться перша буква цього слова
і перегортається).
– квантор
загальності. Означає “для будь якого”,
“для кожного”, “для всіх”. Походить
від англійського слова
Any
–
будь
який (береться перша буква цього слова
і перегортається).
 –
квантор існування. Означає “існує”,
“знайдеться”, “можна вказати”. Походить
від англійського слова Existence
–
існування.
–
квантор існування. Означає “існує”,
“знайдеться”, “можна вказати”. Походить
від англійського слова Existence
–
існування.
Використання
цих символів дозволяє значно скоротити
запис багатьох формуліровок. Запишемо,
наприклад, за допомогою кванторів таке
твердження: “для будь якого додатного
числа
 знайдеться інше додатне число
знайдеться інше додатне число
 ,
яке більше, ніж
”.
Воно буде мати такий вигляд:
,
яке більше, ніж
”.
Воно буде мати такий вигляд:
 .
.
