Доли. Обыкновенные дроби

Равные части называют долями. Долю называют половиной, - третью, а - четвертью.

Записи вида называют обыкновенными дробями. В дроби число 5 называют числителем дроби, а число 8 – знаменателем дроби. Знаменатель показывает, на сколько долей делят, а числитель – сколько таких долей взято.

Дроби можно изображать на координатном луче. Например:

Отрезок ОА равен единичного отрезка ОЕ.

С равнение дробей

На координатном луче равные дроби соответствуют одной и той же точке (смотреть рисунок):

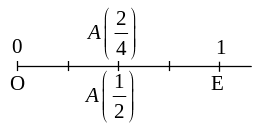
Две равные дроби обозначают одно и то же дробное число. Дробные числа можно сравнивать, складывать, вычитать, умножать и делить.

Из двух дробей с одинаковыми знаменателями меньше та, у которой меньше числитель, и больше та, у которой больше числитель.

Точка на координатном луче, имеющая координату, лежит слева от точки, имеющей большую координату.

Правильные и неправильные дроби

В дроби числитель меньше знаменателя. Такие дроби называют правильными. В дроби числитель равен знаменателю, а дроби числитель больше знаменателя. Такие дроби называют неправильными.

Правильная дробь меньше единицы, а неправильная дробь больше или равна единице.

С ложение и вычитание дробей с одинаковыми знаменателями

При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же. С помощью букв правило сложения можно записать так:

.

При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же.

С помощью букв правило вычитания можно записать:

Деление дробей

С помощью дробей можно записать результат деления двух любых натуральных чисел. Если деление выполняется нацело, то частное является натуральным числом. Если же нацело разделить нельзя, то частное является дробным числом. Например,

З апишем число 3 в виде дроби со знаменателем 5. Для этого надо найти такое число, при делении которого на 5 получалось бы 3. Таким числом является , то есть 15. Значит, .

Любое натуральное число можно записать в виде дроби с любым натуральным знаменателем. Числитель этой дроби равен произведению числа и этого знаменателя.

Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные. С помощью букв это равенство можно записать:

Смешанные числа

Чтобы из неправильной дроби выделить целую часть, надо:

1) разделить с остатком числитель на знаменатель;

2) неполное частное будет целой частью;

3) остаток (если он есть) дает числитель, а делитель – знаменатель дробной части.

З апись числа, содержащую целую и дробную части, называют смешанной. Смешанное число можно представить и в виде неправильной дроби.

Чтобы представить смешанное число в виде неправильной дроби, надо:

1) умножить его целую часть на знаменатель дробной части;

2) к полученному произведению прибавить числитель дробной части;

3) записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.