II. Тепловая диаграмма для воздуха и продуктов сгорания данного топлива методика построения диаграммы

При практических расчетах часто удобнее пользоваться не только таблицами, но и диаграммами. Такие диаграммы могут быть построены, если использовать соотношения, положенные в основу составления таблиц.

Для построения диаграммы для воздуха (рис. 3) по горизонтальной оси отложим температуру (например, в градусах Цельсия), а по верти­кальной—энтальпию H и логарифм относительного давления lg π₀, за­тем нанесем кривые зависимости H, lg π₀ и µRT от температуры для

моля воздуха. По такой диаграмме можно производить те же расчеты, что и по Н, S-диаграмме для воздуха, причем она положительно отли­чается от последней своей простотой: вместо большого количества кри­вых, нанесенных на Н, S-диаграмму, здесь имеются две основные кри­вые и одна вспомогательная прямая.

Для определения адиабатных перепадов теплоты требуется лишь вспомогательная шкала, по которой можно отсчитать логарифмы степе­ни изменения давления в адиабатном процессе lg φ. Следует заметить, что кривая логарифма относительных давлений lg π₀ может быть ис­пользована для определения изменения энтропии в реальном процессе. В самом деле, для изоэнтропного процесса справедливо уравнение (5):

где e — основание натуральных логарифмов; lg e = 0,43429; µR — моль­ная газовая постоянная, равная 8,31441 кДж/(кмоль∙К).

Следовательно,

(21)

Для изоэнтропного процесса имеем

(22)

где S_2s⁰ — значение S⁰ при температуре газа, соответствующей концу изоэнтропного процесса; S₁⁰ — значение S⁰ при температуре газа, соот­ветствующей началу изоэнтропного процесса.

Для реального адиабатного процесса, протекающего при тех же дав­лениях p₁ и р₂ и той же начальной температуры.

(23)

где S₂⁰ — значение S⁰ при температуре газа, соответствующей концу ре­ального процесса.

Вычитая из уравнения (23) уравнение (22), получаем

S₂ – S₁ = S₂⁰ – S_2s⁰ , (24)

т. е. изменение энтропии в реальном процессе равно разности значений S⁰, соответствующих температурам газа в конце реального и изоэнтроп­ного процессов (при одинаковом отношении давлений).

Последнее равенство после подстановки значений S⁰ из уравнения (21) примет вид

S₂-S₁=19,144(lgπ ₀₂-lg^h _02s), (25)

т. е. изменение энтропии определяется через значения логарифма отно­сительного давления.

С целью составления подобной диаграммы для продуктов сгорания данного топлива необходимо по составу этого топлива рассчитать объ­емный состав продуктов его сгорания при коэффициенте избытка воз­духа α=1. Затем, пользуясь значениями энтальпии и логарифма отно­сительного давления для компонентов N₂, CO₂, Н₂O и O_2, приведенны­ми в табл. II.1—II.6, по правилу смешения следует определить H = µh и lgπ₀ для продуктов рассчитанного состава при различных темпера­турах с интервалом 50—100°С.

Имея значения энтальпии и логарифм относительного давления и для воздуха (табл. II.1) и для продукта сгорания топлива без избытка воздуха (табл. II.7), можно построить на одной диаграмме кривые H = µh и lg π₀ в функции температуры для этих двух газовых смесей (воздуха и продукта сгорания) ¹.

Будем теперь рассматривать газообразный продукт сгорания дан­ного топлива с любым избытком воздуха как смесь газообразного про­дукта сгорания топлива при α=1 и влажного воздуха. При этом, зада­ваясь значениями α (например, 2, 3, 4, 5), можно определить объемную долю этого продукта сгорания при α=1 и воздуха в данной смеси. Та­кой расчет очень прост.

Определив теоретическое количество воздуха, необходимого для сго­рания топлива L₀, объем водяных паров в этом количестве воздуха и общий объем продуктов сгорания V⁰ при α=1 легко найти состав газов при любом значении α:

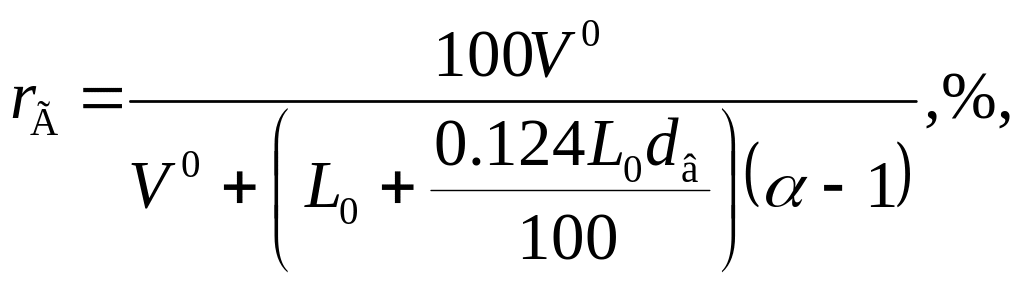
где r_г— объемная доля продуктов сгорания при α = 1; r_в — объемная доля воздуха; d_B — количество водяных паров в граммах на нормаль­ный кубический метр воздуха (согласно нормам расчета котлоагрегатов принято d_B = 8 г/м³).

Если объемную долю воздуха в продукте сгорания топлива принять в качестве параметра, то значения энтальпии и логарифма относитель­ного давления данной смеси определятся линейной интерполяцией меж­ду значениями этих величин для влажного воздуха и для продуктов сгорания топлива при α=1, т. е.

Н_1смеси =Н_в + (H_α=1 —Н_в)(1— r_в).

Иными словами, если интервалы между кривыми энтальпии и кри­выми lg π₆ для продуктов сгорания при α=1 и влажного воздуха раз­делить на п равных частей и соответствующие точки соединить плав­ными кривыми, то полученные кривые будут соответствовать продукту сгорания, содержащему 1/n, 2/п, 3/п ... объемных долей воздуха.

Практически достаточно разделить интервалы на 10 частей, чтобы интерполяция была вполне надежной. Для выбора кривой Н и кривой lgπ₀, соответствующих продукту сгорания с данным избытком воздуха, достаточно нанести на диаграмму кривую зависимости r_в от α, рассчи­танную описанным выше способом.

Для определения молекулярной массы ц и плотности р газообраз­ного продукта сгорания при нормальных условиях и любом значении а на диаграмму, наносят две прямые: µиρ.

В качестве примера в табл. II.7 приведены рассчитанные по правилу смешения значения энтальпии и логарифма относительного давления для продуктов сгорания ряда топлив при α=1.

Диаграмма, подобная описанной, может быть построена для продук­тов сгорания любого топлива (твердого, жидкого и газообразного), в любом удобном и обеспечивающем высокую точность расчета масштабе. Использование такой диаграммы оправдывается исключительной прос­тотой ее построения, высокой точностью и удобством пользования при практических расчетах. Диаграмма может быть рекомендована в тех случаях, когда производятся многочисленные расчеты процессов с про­дуктами сгорания данного топлива.