МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

МИНИСТЕРСТВО ПРОМЫШЛЕННОЙ ПОЛИТИКИ УКРАИНЫ

ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ПОДГОТОВКИ И ПЕРЕПОДГОТОВКИ

КАДРОВ ПРОМЫШЛЕННОСТИ

«Детали машин в примерах»

учебное пособие

для студентов специальности 7.090218

«Металлургическое оборудование»

Разработал

ст. преподаватель ЛАВРЕНОВ Е,М,

Днепропетровск

ГИПОпром

2008

Детали машин в примерах Введение

В данном учебном пособии представлены примеры решения конкретных задач по расчету деталей машин. В основу положены публикации в учебных изданиях по курсу «ДЕТАЛИ МАШИН» авторов: Иванова М.Н., П.Г. Гузенкова П.Г., Андриенко Л.А., Байкова Б.А., МГТУ им. Н.Э. Батмана.

Примеры представлены по темам учебной программы по курсу «ДЕТАЛИ МАШИН». Данное учебное пособие может быть полезным при решении практических задач при выполнении студентами курсовых и дипломных проектов.

Тема 2 фрикционные передачи

П ример расчета 2.1 Рассчитать цилиндрическую фрикционную передачу (рис.2.1) для привода ленточного транспортера при условии, что ведущее колесо передает мощность Р=2 кВт при угловой скорости =102 рад/с ведомому колесу, вращающемуся с угловой скоростью =34 рад/с.[1]

Решение. Назначаем материалы колес: меньшего — текстолит ПТК, а большего — сталь 45.

Передаточное отношение передачи

102/34=3.

Крутящий момент Т₁, передаваемый ведущим колесом

Рис.2.1

=2∙10³/102=19,6Н∙м.

Определим диаметр меньшего колеса из условия контактной прочности. Примем коэффициент запаса сцепления колес =1,25; коэффициент трения по длине контактной линии =0,3; коэффициент неравномерности распределения нагрузки по длине контактной площадки =1,1; коэффициент длины контактной площадки =0,3; допускаемое контактное напряжение сжатия для текстолитового колеса =100МПа, модуль упругости для меньшего колеса (текстолит) Е₁=6∙10³ МПа, для большего колеса (сталь) Е₂=2,15∙10⁵ МПа.

Приведенный модуль упругости Е определим по формуле:

=2∙6∙10³∙2,15∙10⁵/(6∙10³+2,15∙10⁵)=1,17∙10⁴ МПа.

После подстановки в правую часть формулы (10.18) числовых значений получим

=0,08м=80мм.

Диаметр большего колеса

=3∙80=240 мм.

Ширина колес

мм.

Остальные размеры колес принимают конструктивно.

Тема 3 Зубчатые передачи

Пример расчета 3.1 Расчет одноступенчатого цилиндрического редуктора [1].

1.Рассчитать и спроектировать одноступенчатый цилиндрический косозубый редуктор общего назначения по следующим данным:

Мощность на быстроходном валу Р₁=2,2 кВт.

Частота вращения быстроходного вала n₁=1425 мин^-1.

Передаточное число и=1,25.

Срок службы передачи t=35000 часов.

Редуктор изготовлен в отдельном корпусе, нагрузка постоянная, но во время пуска она кратковременно повышается в 1,6 раза по сравнению с номинальной. Быстроходный и тихоходный валы редуктора соединяются с валом электродвигателя и рабочим валом машины с помощью упругих пальцевых муфт.

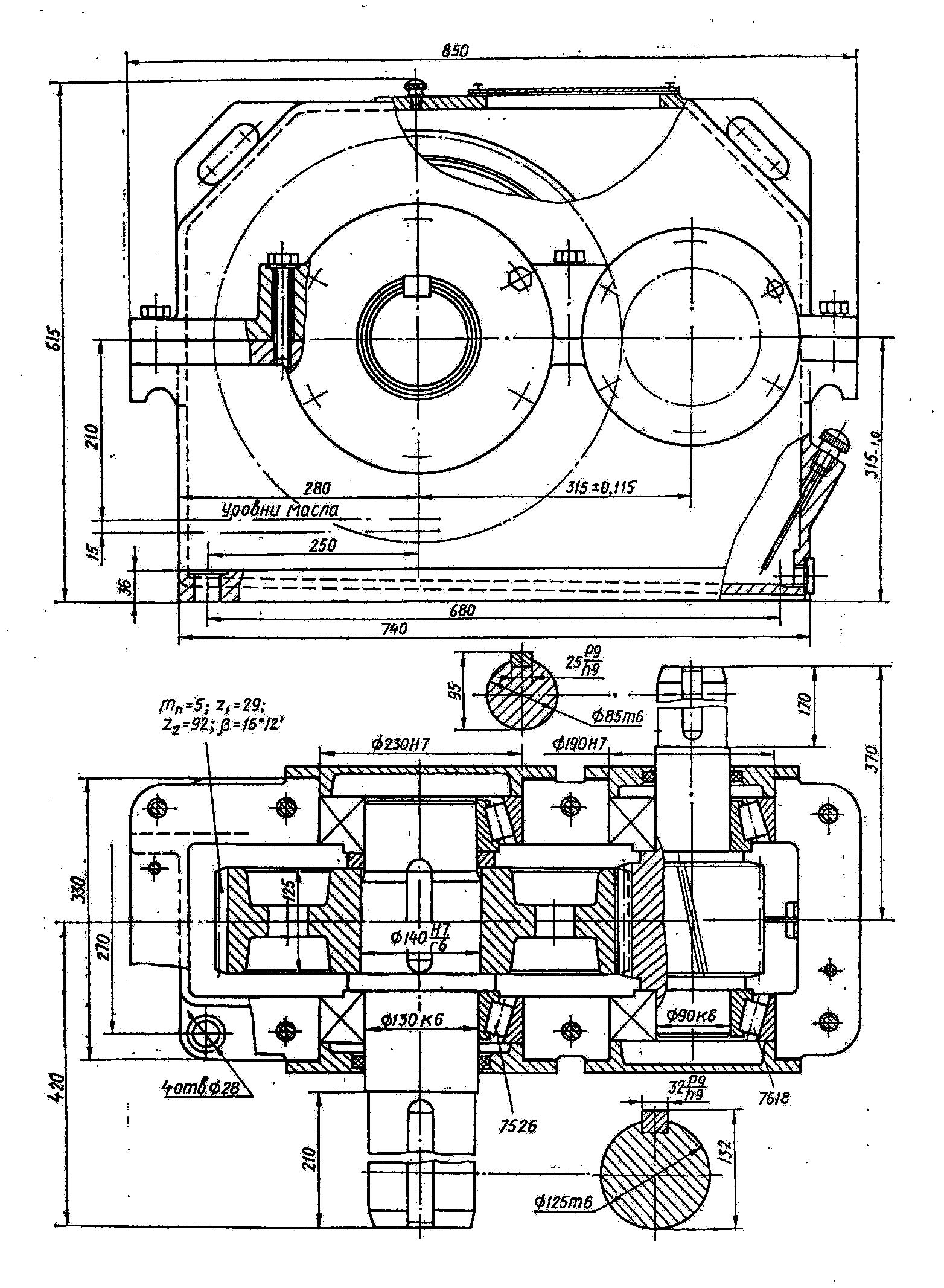
Кинематическая схема редуктора представлена на рис.3.1.

Исходные параметры расчета.

Крутящий момент на быстроходном (ведущем) валу

, (3.1)

где Т₁-в Н·м; Р₁- в Вт; ω₁-угловая скорость быстроходного вала, рад/с.

, здесь n₁-в мин^-1; рад/с.

По формуле (3.1) определим

Крутящий момент на тихоходном валу

здесь - коэффициент полезного действия одноступенчатой зубчатой передачи на подшипниках качения в зависимости от конструкции и 6-й и 7-й степени точности с жидкой смазкой.

Проектировочный расчет зубьев передачи на контактную прочность.

Принимаем: профиль зуба эвольвентный. Основные параметры зубчатой передачи согласно СТ СЭВ229-75. Угол профиля исходного контура СТ СЭВ308-78 α=20˚, без смещения исходного контура.

Межосевое расстояние определим по формуле

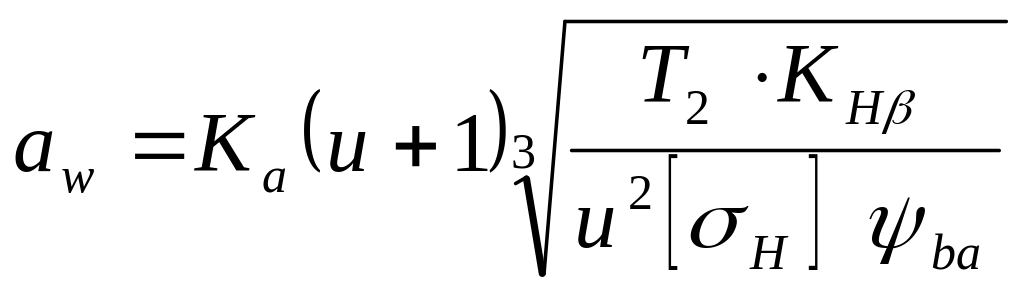, (3.2)

где К_а – Рис.3.1.Схема цилиндрического одноступенчатого косозубого редуктора

Примечание: размеры представленные на рис.1. не отражают результаты расчета.

коэффициент неравномерности нагрузки по ширине колеса; [σ_Н]- расчетное допускаемое контактное напряжение, МПа; ψ_ва –коэффициент ширины колеса относительно межосевого расстояния.

Принимаем для изготовления колеса и шестерни – сталь 40Х, Термообработка: колесо – улучшение НВ240…271; МПа; МПа; шестерня –закалка ТВЧ до твердости НRC48…56; МПа; МПа. Коэффициент - определим по графику в зависимости от коэффициента

здесь - принимаем из ряда стандартных величин в зависимости от положения колес относительно опор. Принимаем .

, (3.3)

где - базовый предел контактной выносливости поверхностей зубьев, МПа; - коэффициент безопасности; - коэффициент долговечности.

Значение определим по табл.3.1

Таблица 3.1. Значения при υ≤5 м/с

Термическая обработка	Твердость поверхности зубьев	, МПа
Нормализация или улучшение	ННВ≤НВ350	2ННВ+70
Объемная закалка	ННRC=НRC40…50	18ННRC+150
Поверхностная закалка	ННRC=НRC40…56	17ННRC+200
Цементация или нитроцементация	ННRC=НRC54…64	23ННRC
Азотирование	ННV=НV550…750	1050

Для колеса НВ<350 МПа

Для шестерни при НRC48…56 МПа.

Принимаем =1,1 при термообработке улучшение и =1,2 при поверхностной закалке, цементации.

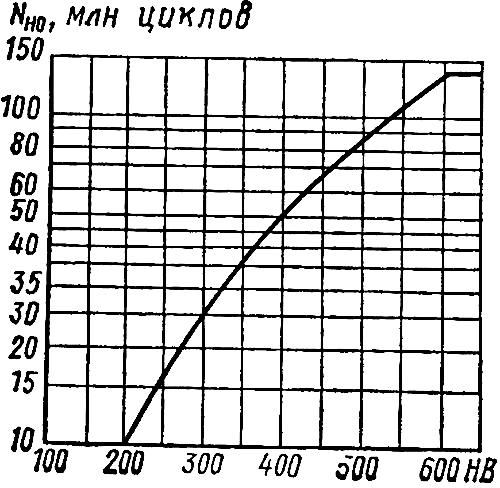
- определим из рис.3.2 в зависимости от отношения , где - базовое число циклов, определяемое по графику рис. 3.3.

- при постоянной нагрузке

Рис.3.2

Рис.3.3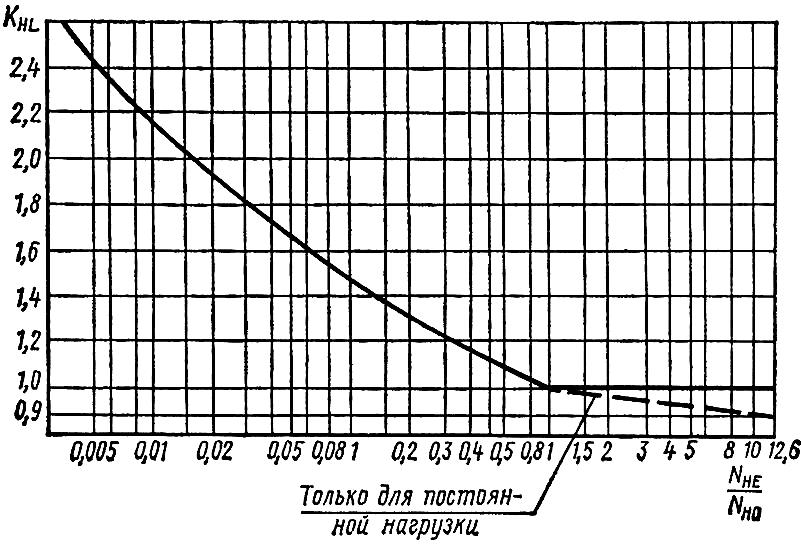

При постоянной нагрузке

,

где n-частота вращения того из колес, по материалу которого определяют [σ]_Н, мин^-1; t =35000 часов – число часов работы передачи за расчетный срок службы; с=1 число зацеплений зуба за один оборот колеса.

По графику 3.3 при НВ240 N_НО=1,5·10⁷.

Так как N_НЕ> N_НО, то из рис. 3.2 K_HL=1,0.

Для шестерни также N_НЕ> N_НО, (так как n₁>n₂) и K_HL=1,0.

По формуле (3.3)

Для колеса МПа

Для шестерни МПа.

[σ]_H для прямозубых передач определяется раздельно для шестерни и колеса и в качестве расчетного принимают меньшее из них. При расчете зубьев косозубых и шевронных колес

(3.4)

где - меньшее из двух допускаемых напряжений.

По формуле (3.4) МПа.

Так как 606,15МПа МПа, то принимаем

МПа.

По формуле (2.1) определяем межцентровое расстояние

мм.

Вычисление a_W округляем в большую сторону до стандартного СТ СЭВ 229-75 и принимаем a_W=50 мм.

Рабочая ширина колеса мм.

Выбираем модуль

мм,

что соответствует СТ СЭВ310-76.

Минимальный угол наклона зубьев

.

что в рекомендуемых пределах (для косозубых колес β=8…18^о).

Суммарное число зубьев.

.

Полученное округляем в меньшую сторону до целого =97.

Действительное значение угла наклона зубьев.

.

Число зубьев шестерни

.

Значение Z₁ округляем в ближайшую сторону до целого. Принимаем Z₁=43.

Число зубьев колеса

.

Фактическое передаточное число

.

Отклонение от заданного передаточного числа

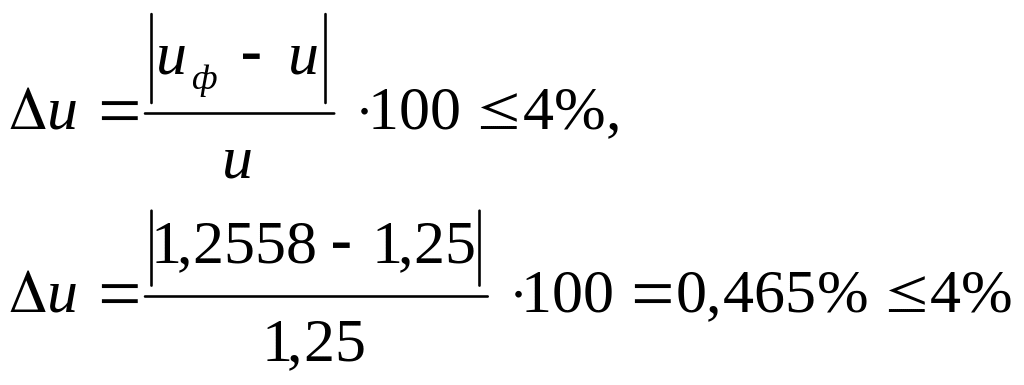
Делительные диаметры:

шестерни

мм

колеса

мм

Межосевое расстояние

мм.

Проверочный расчет зубьев передачи на контактную прочность.

Расчет производим по формуле:

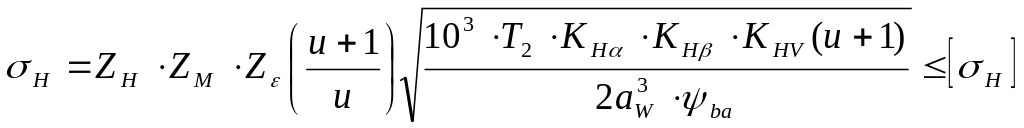(3.5)

где σ_Н, [σ_Н] – расчетное и допускаемое контактное напряжение, МПа.

Z_Н – коэффициент, учитывающий форму сопряженных поверхностей зубьев;

Z_М – коэффициент, учитывающий форму сопряженных поверхностей зубьев;

Z_ε – коэффициент, учитывающий суммарную длину контактных линий;

К_Hα –коэффициент неравномерности распределения нагрузки;

К_НV – коэффициент динамичности нагрузки.

Определяем значения величин, входящих в формулу(3.5). Для прямозубой передачи . При расчете косозубой передачи принимаем основной угол наклона линии зуба . Тогда

.

Коэффициент для прямозубых передач

для косозубых передач .

Коэффициент торцевого перекрытия

тогда .

По графику рис.3.4,а коэффициент .Коэффициент

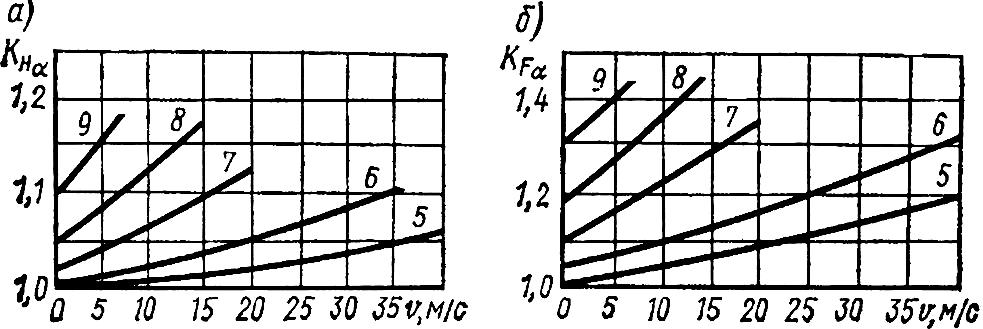
рис.3.4

(определен ранее). По таблице 3.2 коэффициент

Таблица 3.2 Значения коэффициента динамической нагрузки

Степень точности	Твердость поверхностей зубьев	v, м/с
		1	2	4	6	8	10
6-я	а б
7-я	а б
8-я	а б
9-я	а б

Примечания:1. Твердость поверхности зубьев: а) Н₁≤НВ350 и Н₂≤НВ350 или Н₁≥HRC45 и Н₂≤НВ350; б) Н₁≥HRC45 и Н₂≥HRC45. 2. Значения К_Hv в числителе относятся к прямозубым передачам, а в знаменателе – к косозубым.

Тогда по формуле (3.5)

МПа

МПа.

Контактная прочность удовлетворена.

Проверочный расчет зубьев передачи на выносливость по напряжениям изгиба.

Расчет по напряжениям изгиба производим по формуле

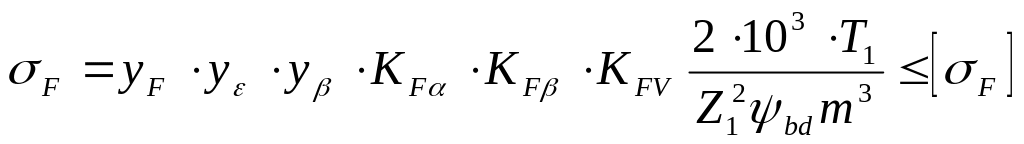(3.6)

где - расчетное и допускаемое напряжение изгиба, МПа

y_F – коэффициент формы зуба;

y_ε – коэффициент перекрытия зубьев;

y_β – коэффициент наклона зубьев;

К_Fα – коэффициент распределения нагрузки между зубьями

К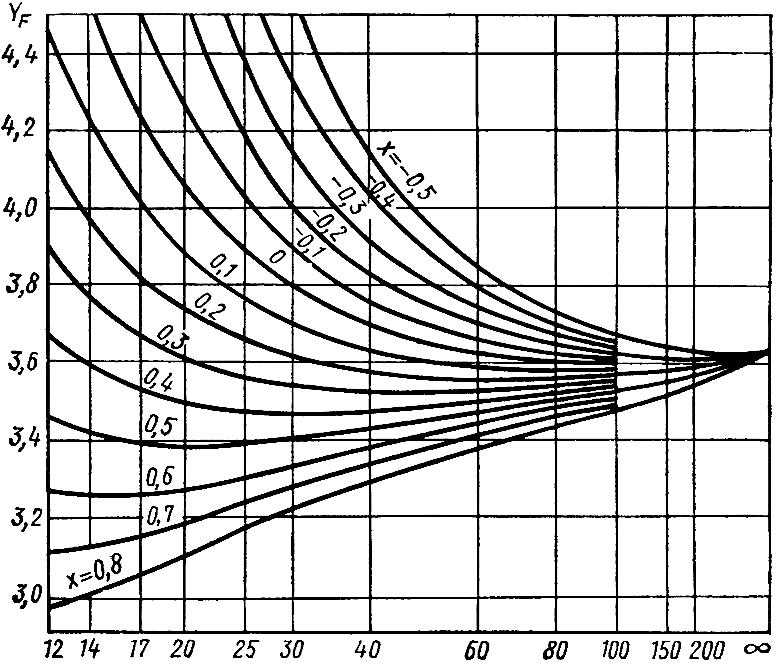 _Fβ – коэффициент неравномерности распределения нагрузки по ширине венца зубчатого колеса.

К_FV – коэффициент динамической нагрузки.

В формуле (3.6) Т₁ в Н·м; т – в мм.

Эквивалентное число зубьев шестерни

Э

Рис. 3.5

тому числу зубьев по графику 3.5 соответствует коэффициент формы зубьев шестерни Y_F=3,7.

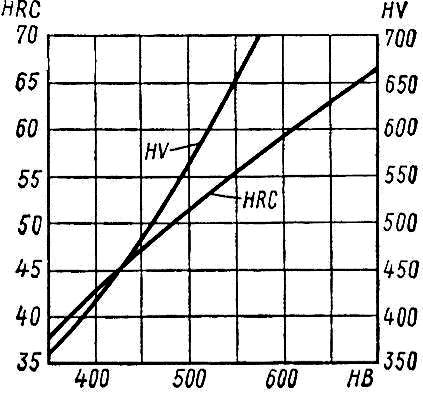К оэффициент y_ε=1 (см.с.189[1]). Коэффициент y_β (см.с.190[1]); .

Окружная скорость передачи

3,31м/с.

Для этой скорости V значения коэффициентов и приняты правильно.

П

Рис. 3.6

о графику рис.3.4,б при НВ₂<350 коэффициент К_Fα=1,05. При НВ460 (из рис.3.6 НRС50≈НВ460) и ψ_bd=0,83 по графику V рис.3.7 при НВ₂<350 коэффициент К_Fβ =1,06. По табл.3.4 К_FV =1,06.

Д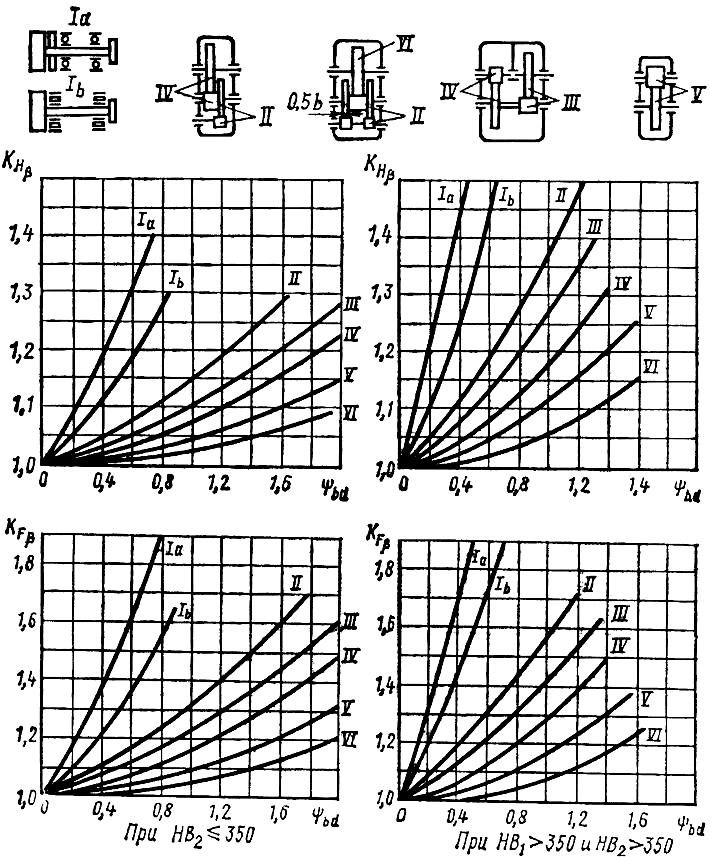 опускаемые напряжения изгиба

, (3.7)

где - предел выносливости зубьев при изгибе, соответствующий числу циклов напряжений базовому, МПа.

- коэффициент безопасности.

- коэффициент, учитывающий влияние двухстороннего приложения нагрузки (при одностороннем действии =1);

- коэффициент долговечности.

П

Рис. 3.7

ри НВ≤350 , а также для зубчатых колес со шлифованной переходной поверхностью зубьев

(3.8).

П

рис.3.7

ри НВ>350 и не шлифованной переходной поверхности

,

где - базовое число циклов (для всех сталей =4·10⁶);

- эквивалентное число циклов.

По табл.3.6 для колеса

Таблица 3.6.Пределы выносливости

Вид термообработки и марка стали	Твердость зубьев HRC		, МПа
	на поверхности	в сердцевине
Цементация легированных сталей: содержание Ni более 1%,Cr 1% и менее (например, 20ХН2М, 12Х2Н3А и др. стали марок 18ХГТ, 30ХГТ, 12ХН4А и др. Нитроцементация легированных сталей: 25ХГМ 25ХГТ,30ХГТ и др.	57…63	32…45	950 800 750
Закалка при нагреве ТВЧ по всему контуру: стали пониженной прокаливаем ости (например 55ПП) стали марок 60ХВ, 60Х. 60ХН и др. стали марок 35ХМА, 40Х, 40ХН и др.	58…62 54…60 48…60	28…35 25…35 25…35	900 700 600
Нормализация или улучшение	НВ	180…350	1,35НВ+100
Азотирование легированных сталей	-	24…40	18HRCсердц+50

МПа.

Для шестерни

=600МПа

В нашем случае для колеса

Поэтому по формуле (3.8) =1

По формуле (3.7) для колеса

МПа,

для шестерни

МПа.

По графику рис.3.5 для колес, изготовленных без смещения (коэффициент смещения Х=0), при эквивалентных числах зубьев шестерни

колеса

находим для шестерни , для колеса Расчет выполняем по тому колесу пары, у которого меньше отношение . В нашем случае

Расчет выполняем по колесу.

По формуле (2.6)

МПа≤[σ_F]=212 МПа.

Условие прочности по напряжениям изгиба обеспечена.

Проверка прочности зубьев при перегрузках

Максимальные контактные напряжения

где - максимальное расчетное напряжение при перегрузке зубьев максимальным моментом ; - допускаемое максимальное контактное напряжение для зубьев, МПа; - расчетное контактное напряжение, вызываемое расчетным моментом Т₁;

- при нормализации, улучшении или объемной закалке зубьев, где - предел текучести материала;

=HRC 40 –при цементации зубьев и закалке т.в.ч.

Для колеса МПа

Для шестерни =50·40=2000МПа

МПа< =1652 МПа.

Статическая контактная прочность при перегрузке обеспечена.

Максимальные напряжения изгиба

(3.9)

где - максимальное расчетное напряжение на изгиб в зубьях колес при перегрузке максимальным моментом ;

- допускаемое максимальное напряжение на изгиб;

- расчетное напряжение на изгиб для зубьев, вызываемое расчетным моментом .

При НВ≤350, ; при НВ>350

где - предел прочности материала.

Расчет зубьев по формуле (3.9) производят для менее прочного колеса передачи.

Для колеса МПа.

МПа < =472МПа.

Размеры основных элементов зубчатого зацепления.

В соответствии с СТ СЭВ 308-76 и ГОСТ 13754-68 коэффициент высоты головок зубьев ; коэффициент радиального зазора С^*=0,25; высота головки зубьев мм, высота ножек зубьев , высота зубьев мм.

Делительный диаметр d, диаметр вершины d_а и диаметр впадин d_f

для шестерни:

d₁ =44,329 мм (вычислен ранее).

мм

мм

для колеса

d₂= 55,670 мм (вычислен ранее).

мм

мм.

Ширина колеса в₂=в=20 мм.

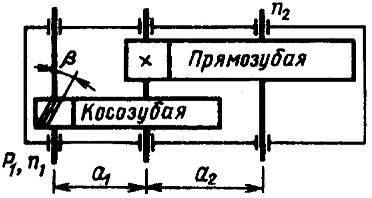Пример расчета 3.2 Рассчитать редуктор, установленный в приводе конвейера (рис. 3.8): Р₁=4,5 кВт, п₁=960мин^-1 , передаточное отношение i=20; редуктор должен работать 8 ч в сутки, 300 дней в году в течение 10 лет; режим нагружения II—рис. 8.42; кратковременная перегрузка не превышает двух номинальных моментов. Редуктор изготовлен в отдельном закрытом корпусе; смазка—погружением колес в м

Рис. 3.8

асляную ванну [2].

Решение. Для получения небольших габаритов и невысокую стоимость редуктора, выбираем для изготовления колес и шестерен легированную сталь 40Х (поковка). Назначаем для колес термообработку: улучшение 230...260 НВ, σ_В=850 МПа, σ_Т=550МПа, для шестерни второй ступени— улучшение 260...280 НВ, σ_В=950МПа, σ_Т=700 МПа; зубьям шестерни первой ступени—азотирование поверхности 50...59 HRC при твердости сердцевины 26...30HRC, σ_В=1000 МПа, σ_Т=800 МПа. При этом обеспечивается приработка зубьев обеих ступеней

Определяем допускаемые напряжения. Допускаемые контактные напряжения по табл.3.7 для колес обеих ступеней σ_Hlim =2HB+70=2·240+70=550 МПа; для шестерни первой ступени σ_Hlim =1050 МПа.

Коэффициент безопасности: для первой ступени s_H=1,2, для второй ступени s_H=l,l.

Число циклов напряжении для колеса второй ступени, по формуле, при с=1 N_k=60nt_Σ=60·48·24000=7·10⁷. Здесь n=960/20=48 мин^-1—частота вращения выходного вала, t_Σ=10·300·8=24000 ч—срок службы передачи.

По графикам рис 3.9, для 245 НВ (среднее) N_HG≈1,5·10⁷ для 50...59 HRC (≈550 НВ) N_HG≈10⁸.

По табл. 3.8, µ_H=0,25. По формуле (8.64), для колеса второй ступени N_НЕ=0,25·7·10⁷=1,75·10⁷.

Сравнивая N_HE и N_HG, отмечаем, что для колеса второй ступени N_HE>N_HG. Так как все другие колеса вращаются быстрее, то аналогичным расчетом получим и для них N_НE>N_HG. При этом для всех колес передачи Z_Н=1.

Допускаемые контактные напряжения для второй ступени определяем по материалу колеса, как более слабому. По формуле

[σ_H]=550/1,1=500 МПа.

Для колеса первой ступени также [σ_H]₂=500 МПа, а для шестерни [σ_H]₁=1050/1,2=875 МПа.

Допускаемое контактное напряжение для первой ступени, у которой H₁>350НВ, а Н₂<350 НВ, по формуле [σ_H]=(875+500)/2≈690МПа>1,25[σ_H]₂,принимаем [σ_H]=1,25[σ_H]₂=625 МПа.

Таблица 3.7

Марка стали*	Размер сечения s, мм, не более	Механические свойства (при поверхностной закалке и относятся к сердцевине)				Термообработка	Ориентировочный режим термообработки (3—закалка; О—отпуск с указанием температуры нагрева и охлаждающей среды; М—масло; В—вода; Н — нормализация)
		твердость Н**		предел прочности , МПа	предел текучести МПа
		поверхности	сердцевины
Заготовка-поковка (штамповка или прокат)
40	60	192...228 НВ		700	400	Улучшение	З, 840..860° С, В, О, 550...620° С
45	80	170...217 НВ		600	340	Нормализация	Н, 850...870°С,
	100	192...240 НВ		750	450	Улучшение	3, 820...840°С, В, О, 560...600° С
	60	241...285 НВ	—	850	580	»	3, 820...840°С, В, О, 520...530° С
50	80	179...228 НВ	__	640	350	Нормализация	Н, 840...860° С
	80	228...255 НВ	—	700..800	530	Улучшение	3, 820...840° С, О, 560...620° С
40Х	100	230...260НВ	—	850	550	»	3, 830...850° С, О, 540...580° С
	60	260...280НВ	__	950	700	»	3, 830...850°С, О, 500° С
	60	50...59 HRC	26...30HRC	1000	800	Азотирование	То же, с последующим мягким азотированием
45Х	100	230...280 НВ	—	850	650	Улучшение	3, 840…860° С, М, О, 580...640° С
	100...300	163...269 НВ	—	750	500	»	То жe
	300...500	163..269 НВ	—	700	450	»	»
40ХН	100	230...300 НВ	—	850	600	»	3, 820...840° С, М, О, 560...600° С
	100...300 40	≥241 НВ 48...54HRC	—■	800 1600	580 1400	» Закалка	То жe З, 820…840 С, М, О 180…200°С
35ХМ	100	241 НВ	—	900	800	Улучшение	З, 850…870°С, М, О 600…650°С
	50 40	269НВ 45...53 HRC	— —	900 1600	800 1400	» Закалка	То жe З, 850…870°С, М, О 200…240°С
40ХНМА	80 300	≥302 НВ ≥217 НВ	— —	1100 700	900 500	Улучшение »	З, 830…850°С, М, О 600…620°С То же
35ХГСА	150 60 40 30	235 НВ 270 НВ 310 НВ 46...53HRC	— — — —	≥760 980 1100 1700...1950	≥500 880 1350… 1600	» » » Закалка	З, 850…880°С, М, О 640…660°С З, 850…880°С, М, О 500°С То же З, 850…880°С, М, О 200…2560°С
20Х 12ХНЗА 25ХГТ 38ХМЮА	60 60 — —	56...63 HRC 56...63HRC 58...63HRC 57...67 HRC	— — 30...35 HRC	650 900 1150 1050	400 700 950 900	Цементация » » Азотирование	З, О З, О З, О Заготовка-улучшение
Стальное литье
45Л 30ХНМЛ 40ХЛ 35ХМЛ	— — — —	— — — —	— — — —	550 700 650 700	320 550 500 550	Нормализация	Н, О Н, О Н, О Н, О

В обозначениях сталей первые цифры – содержание углерода в сотых процентах; буквы – легирующие элементы; Г- марганец, М – молибден, Н – никель, С –кремний, Х – хром, Ю –алюминий; после буквы – процент содержание этого элемента если оно превышает 1%. Обозначение высококачественных легированных сталей дополняется буквой А; стальное литье – буквой Л в конце.

** При нормализации, улучшении и объемной закалке твердости поверхности и сердцевины близки. Ориентировочно Н≈(0,285 ) НВ.

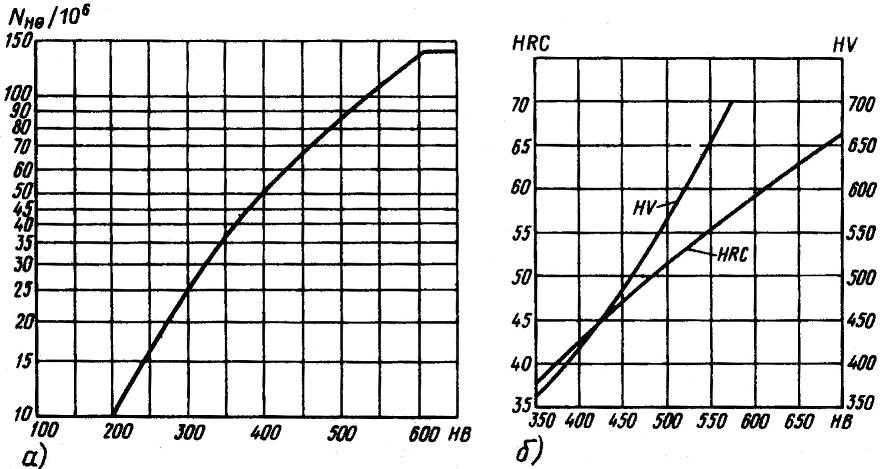
Рис.3.9.

Таблица 3.8 Значения при п = const для типовых режимов нагружения

Режим работы	Расчет на контактную усталость			Расчет на изгибную усталость
	термообработка	т/2		термообработка	т		термообработка	т
0 I II III IV V	Любая	3	1,0 0,50 0,25 0,18 0,125 0,063	Улучшение, нормализация, азотирование	6	1,0 0,30 0,143 0,065 0,038 0,013	Закалка объемная, поверхностная, цементация	9	1,0 0,20 0,10 0,036 0,016 0,004

Допускаемые напряжения изгиба. По табл. 3.9, для колес обеих ступеней

Таблица 3.9

Термообработка	Твердость зубьев Н**			Группа сталей	, МПа			sF	МПа	МПа
	на поверхности		в сердцевине
Нормализация, улучшение Объемная закалка	180...350НВ 45...35HRC			40; 45; 40Х; 40ХН;45ХЦ; 5ХМ и др. 40Х; 40ХН; 45ХЦ;36ХМ и др.	2НВ+70 18HRC+150	1,1	1,8HB 550 900 650 550	1,75	2,8σт 2,8σт	2,74HB 1400 1260 » 1430 1000 »
Закалка т.в.ч. по всему контуру (модуль тп≥3мм) Закалка т.в.ч. сквозная с охватом впадины (модуль тn<3мм*)	56...63HRC 45...55HRC 45...55HRC	25...55HRC » 45...55HRC		55ПП; У6; 35ХМ; 40Х; 40ХН и др. 35ХМ; 40Х; 40ХН и др.	17 HRCпов +200	1,2			40HRCпов 40HRCпов, 40HRCпов, 30HRCпов.
Азотирование	55...67HRC 50...59 HRC	24...40HRC »		35ХЮА; 38ХМЮА; 40Х; 40ХФА; 40ХНМА и др.	1050 » 23HRCпов 23HRCпов 23HRCпов		12HRCсердц+300 1,75
Цементация и закалка Нитроцементация и закалка	55...63HRC 57...63HRC	30...45HRC 30...45HRC		Цементируемые стали всех марок Молибденовые стали 25ХГМ, 25ХГНМ. Безмолибденовые стали 25ХГТ, 30ХГТ, 35Х и др			750 1000 750	1,5	40HRCпов, 40HRCпов. 40HRCпов,	1200 1520 1520

*Распространяется на все сечения зуба и часть тела зубчатого колеса под основанием, впадины.

**Приведен диапазон значений твердости, в котором справедливы рекомендуемые зависимости для пределов выносливости и предельных допускаемых напряжений (рассчитывают по средним значениям твердости в пределах допускаемого отклонения, указанного в табл. 8.8); HRC_пов—твердость поверхности, HRC_сердц—твердость сердцевины.

σ_HFlim=1,8·240=432 МПа; для шестерни первой ступени

σ_HFlim=12·28+300=636 МПа; для шестерни второй ступени

σ_HFlim=1,8·270=486 МПа.

Определяем [σ_F] по формуле (8.67). Предварительно по формуле (8.71) и табл. 3.8 для колеса второй ступени при т=6 и ранее найденных значениях N_k получим N_FЕ=0,14·7·10⁷=0,98 10⁷> N_FG=4·10⁶. При этом Y_N=l. Аналогично и для всех других колес и шестерен получим Y_N=1. Передача не реверсивная, Y_A=1.

По табл. 3.9, S_F=1,75. Для обоих колес

[σ_F]=432/1,75=246 МПа; для шестерни второй ступени

[σ_F]= 486/1,75=278 МПа; для шестерни первой ступени

[σ_F]=636/1,75=363 МПа.

Допускаемые напряжения при кратковременной перегрузке—табл. 3.9. Предельные контактные напряжения для колес обеих ступеней

[σ_Н]_max=2,8[σ_т]=2,8·550=1540 МПа; для шестерни второй ступени

[σ_Н]_max=2,8·700=1960 МПа, для шестерни первой ступени

[σ_Н]_max=30·55=1650 МПа.

Предельные напряжения изгиба для обоих колес [σ_F]_тах=2,74·240=685 МПа; для шестерни второй ступени [σ_F]_тах=2,74·270=740 МПа; для шестерни первой ступени [σ_F]_тах 1000 МПа.

3. Распределяем передаточное отношение между первой и второй ступенями редуктора (рис. 3.10): и₁=6; и₂=i/и₁=20/6=3,34.

4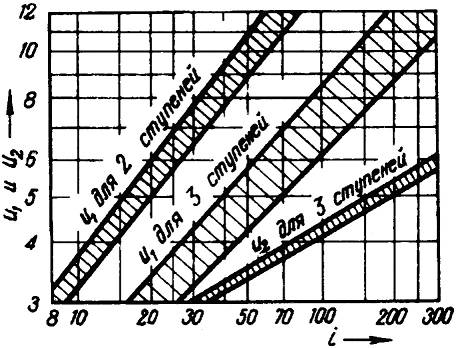 . Крутящие моменты: на входном валу при

ω

Рис 3.10

₁=πn/30=π960/30=100с^-1, Т₁=Р₁/ ω₁=4,5·10³/100=45 Н·м=45·10³ Н·мм; на промежуточном валу Т_п=Т₁и₁η= 45·6·0,97=262 Н·м=262·10³ Н·мм, КПД - η=0,97); на выходном валу редуктора Т_ш=Т₁iη²=45·20·0,972=847 Н·м=847·10³ Н·мм.

5. Вначале рассчитываем вторую прямозубую пару, как более нагруженную и определяющую габариты редуктора. Условимся обозначать здесь и далее предварительно выбранные или рассчитанные параметры дополнительным индексом—штрих. По рекомендации табл. 3.10 принимаем Таблица 3.10

Редукторы при расположении колес относительно опор (см. рис. 8.13)	Рекомендуемые значения	Твердость рабочих поверхностей зубьев
		Н2≤350НВ или Н1 и Н2≤350НВ	Н1 и Н2>350НВ
Симметричное Несимметричное Консольное	ψbа ψbа ψbа	0,3...0,5 1,2...1,6 0,25...0,4 1,0„.1,25 0,2...0,25 0,6...0,7	0,25...0,3 0,9...1,0 0,2...0,25 0,65...0,8 0,15...0,2 0,45...0,55

Примечания: 1. Для шевронных колес при b_w, равной сумме полушевронов, ψ_bа увеличивают в 1,3...1,4 раза. 2. Для подвижных колес коробок скоростей ψ_bа=0,1,..0,2. 3. Большие значения—для постоянных и близких к ним нагрузок. 4. Для многоступенчатых редукторов, в которых нагрузка увеличивается от ступени к ступени, в каждой последующей ступени значения ψ_bа, ψ_bd принимают больше на 20...30%, чем в предыдущей. Это способствует хорошему отношению размеров колес по ступеням (см. § 8.9). Если при расчете выбирают ψ_bа, то расчетное значение b_w проверяют по максимально допускаемому значению

=0,4. При этом по формуле

=0,5·0,4(3,34+l)=0,868 (< =l,25; см. табл. 3.10) и по графику

рис.3.7 находим К_Нβ≈l,06. Далее находим Е_пр=2,1·10⁵ МПа; ранее было найдено [σ_Н]=500 МПа;

Т₂=Т_т=847·10³ Н·мм. Подставляя в формулу, находим

мм.

Округляя по ряду R_a 40 (см. с. 136) до а₂=200 мм, находим b'_w= a₂=80мм. По табл. 3.11 принимаем =30 и находим модуль т'=b'_w/ =80/30= 2,66 мм. По табл. 3.12 назначаем т=2,5 мм.

Суммарное число зубьев z'_Σ=2a/m=2·200/2,5=160.

Примечание. При расчете прямозубых передач без смещения для сохранения принятого значения а модуль следует подбирать так, чтобы z'_Σ было целым числом.

Число зубьев шестерни z₁=z'_Σ(u'₂+1)=160/(3,34+1)=26,86. Принимаем z_l=31>z_min=l7. Число зубьев колеса z₂=z'_Σ—z_l=160—37=123. Фактическое передаточное число и₂=z₂/z_l=123/37=3,324. При этом =20/3,324=6,02. Делительные диаметры шестерни и колеса d_l=z_lm=31·2,5=92,5 мм; d₂=123·2,5=307,5 мм.

Таблица 3.11

Конструкция	ψт=bw/m, не более
Высоконагруженные точные передачи, валы, опоры и корпуса повышенной жесткости:
Н≤350HB	45...30
Н>350НВ	30...20
Обычные передачи редукторного типа в отдельном корпусе с достаточно жесткими валами и опорами (и другие аналогичные): Н≤350HB	30...20
Н>350НВ	20..15
Грубые передачи, например с опорами на стальных конструкциях (крановые и т.п.) или с плохо обработанными колесами (литые), а также открытые передачи, передачи с консольными валами (конические), подвижные колеса коробок скоростей	15...10

Примечание. Меньшие значения ψ_т — для повторно-кратковременных режимов работы, значительных перегрузок и средних скоростей; большие значения ψ_т — для длительных режимов работы, небольших перегрузок и высоких скоростей.

Таблица 3.12

Ряды	Модуль, мм
1-й	1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25
2-й	1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22

Примечание. Следует предпочитать 1-й ряд.

6. Выполняем проверочный расчет на усталость по контактным напряжениям. Предварительно определяем K_H=K_НβK_Hv. Частота вращения колеса второй, ступени n₃=n₁/i=960/20=48^-1 мин. Окружная скорость v=πd₂n₃/60=π·307,5·10^-3·48/60=0,77 м/с. По табл. 3.13 назначаем 9-ю степень точности.

Таблица 3.13

Степень точности, не ниже	Окружная скорость, м/с, не более		Примечание
	прямозубая	косозубая
6 (высокоточные) 7 (точные) 8 (средней точности) 9 (пониженной точности)	15 10 6 2	30 15 10 4	Высокоскоростные передачи, механизмы точной кинематической связи—делительные отсчетные и т.п. Передачи при повышенных скоростях и умеренных нагрузках или при повышенных нагрузках и умеренных скоростях Передачи общего машиностроения, не требующие особой точности Тихоходные передачи с пониженными требованиями к точности

По табл. 3.14, K_Hv=1,06. Ранее было найдено К_нβ=1,07. При этом К_н=1,07·1,05=1,13.

Учитывая, что для нашего примера α_w=α=20°, sin2α≈0,64 и Т₁=Т_II, находим

МПа≈[σ_H]=500МПа.

Примечание. Если значения [σ_H]=и σ_H расходятся более чем на ±5%, то их можно сблизить путем изменения ширины колес по условию, которое следует из формулы (8.10): .

7. Выполняем проверочный расчет по напряжениям изгиба — формула

Таблица 3.14

Степень точности ГОСТ 1643-81	Твердость поверхностей зубьев	Коэффициенты	v, м/с
			1	3	5	8	10
6	а	Khv	1,03 1,01	1,09 1,03	1,16 1,06	1,25 1,09	1,32 1,13
		Kfv	1,06 1,03	1,18 1,09	1,32 1,13	1,50 1,20	1,64 1,26
	б	Khv	1,02 1,01	1,06 1,03	1,10 1,04	1,161,06	1,20 1,08
		Kfv
7	а	Khv	1,04 1,02	1,12 1,06	1,20 1,08	1,321,13	1,40 1,16
		Kfv	1,08 1,03	1,24 1,09	1,40 1,16	1,64 1,25	1,80 1,32
	б	Khv	1,02 1,01	1,06 1,03	1,12 1,05	1,19 1,08	1,25 1,10
		Kfv
8	а	Khv	1,05 1,02	1,15 1,06	1,24 1,10	1,38 1,15	1,48 1,19
		Kfv	1,10 1,04	1,30 1,12	1,48 1,19	1,77 1,30	1,96 1,38
	б	Khv	1,03 1,01	1,09 1,03	1,15 1,06	1,24 1,09	1,30 1,12
		Kfv
9	а	Khv	1,06 1,02	1,12 1,06	1,28 1,11	1,45 1,18	1,56 1,22
		Kfv	1,11 1,04	1,33 1,12	1,56 1,22	1,90 1,36	- 1,45
	б	Khv	1,03 1,01	1,09 1,03	1,17 1,07	1,28 1,11	1,35 1,14
		Kfv

Примечания: 1. Твердость поверхностей зубьев

а — Н₁≤350HB, Н₂≤350НВ;

Н₁≥45НRC, Н₂≤350НВ;

б— H₁≥45HRC, Н₂>≥45HRC.

2. Верхние числа —прямозубые, нижние—косозубые колеса.

По графику рис.3.5 при х=0 находим: для шестерни =3,87, для колеса Y_FS2≈3,73.

Расчет выполняем по тому из колес пары, у которого меньше [σ_F]/ . В нашем случае [σ_F1]/ =278/3,87=72; [σ_F2]/Y_FS2=246/3,73=66. Расчет выполняем по колесу.

По графику рис. 3.7, K_Fβ=l,15. По табл. 3.14 K_Fv=l,11. При этом K_F=l,15·1,11=1,28. Далее, Н. По формуле, σ_F2=3,73·5665·1,28/(80·2,5)=137 МПа < [σ_F]=246 МПа; Отмечаем, что для данной пары колес основным критерием работоспособности является контактная, а не изгибная прочность.

Выполняем проверочный расчет на заданную перегрузку

=713МПа<1540 МПа.

σ_Fmax=137·2=274 МПа<685 МПа.

Условия прочности соблюдаются.

9. Рассчитываем первую косозубую пару. Этот расчет можно выполнять с учётом или без учета уже известных размеров колес второй ступени редуктора. Во втором случае сохраняется порядок расчета, изложенный выше. При этом приходится выполнять корректировку расчетов в целях уменьшения габаритов и соблюдения условия одновременного погружения колес обеих ступеней в масляную ванну на рекомендуемую глубину. Тот же результат получают быстрее при расчете с учетом размеров колеса второй ступени. Ниже излагается такой расчет.

Назначаем ( )₁=(0,7...0,9)( )₂=240 мм, где (d₂)₂—диаметр колеса второй ступени = /u₁=240/6,02=40 мм; =0,5( + )=140мм соответствует ряду R_a40. В противном случае подбираем новые значения диаметров колес.

Для определения ширины колес b_w решаем уравнение относительно и приняв К_Нβ=1:

=0,2·140=28 мм.

При этом =28/40=0,7 не превышает допускаемых максимальных значений (табл. 3.10).

По табл. 3.11 принимаем =25 и находим m_n= =28/25=1,12.мм.

По табл. 3.12 и рекомендациям назначаем m_n=1,5мм. Принимаем =1,2 и определяем β:sin β΄=π·1,2·1,5/28 = 0,202; β'≈12° — в рекомендуемых пределах.

Далее, z'₁=d₁cosβ/m_n=40·0,978l/l,5≈26>z_min=16 (табл.3.15), z'₂=z'_lu'₁=26·6,02 ≈157.

Таблица 3.15

Коэффициент смещения		Передачи
шестерни х1	колеса х2	прямозубые	косозубые и шевронные
0 0,3 0,5	0 -0,3 0,5	z1>21 14≤z1≤20 и и≥3,5 10≤z1≤30***	z1≥zmin+2* z1≥zmin+2, но не менее 10 и и≥3,5**. Рекомендация не распространяется на передачи, у которых при твердости колеса ≤320 НВ твердость шестерни превышает не более чем на 70 НВ

* Ограничение по подрезанию:

β, град до 12 св. 12 до 17св. 17 до 21 св. 21 до 24 св. 24 до 28

z_min 17 16 15 14 13

β, град св. 28 до 30

z_min 12

** Ограничение по подрезанию:

β, град до 10 св. 10 до 15 св. 15 до 20 св. 20 до 25 св. 25 до 30

z_min 12 11 10 9 8

*** Нижние предельные значения z₁, определяемые минимумом ε_a=1,2 в зависимости от z₂:

z₂ 16 18...19 20...21 22...24 25...28 29

z₁ 16 14 13 12 11 10

Фактическое передаточное число u₁=157/26=6,038. Фактическое передаточное отношение редуктора i=u₁u₂=6,038·3,324=20,07; отклонение от заданного 0,3% меньше допускаемого ±4%.

Уточняем значение β по межосевому расстоянию; cosβ=0,5(z₁+z₂) m_n/a=0,5(26+157)1,5/140=0,9804, β=11°21'40".

1 0. Выполняем проверочный расчет по контактным напряжениям. Предварительно определяем окружную скорость:

v=πd₁n₁/60=π·40·10^-3·960/60≈2 м/с.

По табл. 3.13 назначаем 9-ю степень точности.

П

Рис.3.11

о табл. 3.14 K_Hv=l,04; по графику рис. 3.11, K_Hβ=1,1 и, далее К_H=1,1·1,04=1,144.

По табл. 3.16, К_На=1,13.

Таблица 3.16

Окружная скорость v, м/с	Степень точности	KHα	KFα
До 5 Св; 5 до 10 Св. 10 до 15	7 8 9 7 8 7 8	1,03 1,07 1,13 1,05 1,10 1,08 1,15	1,07 1,22 1,35 1,2 1,3 1,25 1,40

По формуле

=[1,88- 3,2(1/26+1/157)]cosβ=l,7

в рекомендуемых пределах.

По формуле

По формуле, при α_w=α=0°

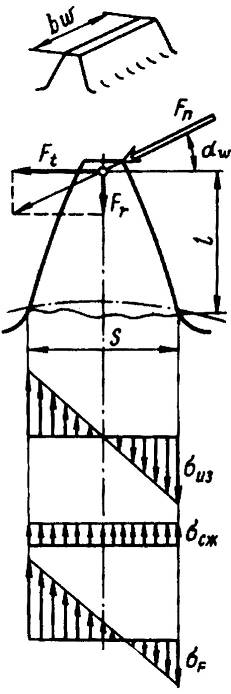=1,18·0,8 МПа≈[σ_H]=625МПа-корректировать b_w не требуется.

11. Проверочный расчет по напряжениям изгиба.

По формуле

z_v1=26/0,9804³≈28; z_v2=157/0,9804³≈167.

По графику риc.3.12 при x=0 находим; для шестерни Y_FS1=3,9, для колеса Y_FS2=3,75. [σ_F1]/Y_FSl=363/3,9=93; [σ_F2]/Y_FS2=246/3,75=70,4 расчет выполняем по меньшему значению, т.е. по колесу.

По табл. 3.17, K_Fα=l,35

По формуле находим Y_Fβ=1,35-0,91/1,7≈0,72.

где Y_β=1-β°/140=1-11,36/140=0,91

По графику рис. 3.11, K_Fβ=1,2, по табл. 3.14, K_Fv=1,08. При этом K_F=1,2·1,08=1,3.

Далее F₁=2T₁/d₁=2·45·10³/40=2250 Н.

П

Рис. 3.12

о формуле

σ_F=3,75·0,72·2250·1,3/(28·1,5)=185 МПа<[σ_F]=240 МПа—условия прочности соблюдаются.

Таблица 3.17

Окружная скорость v, м/с	Степень точности	KHα	KFα
До 5 Св; 5 до 10 Св. 10 до 15	7 8 9 7 8 7 8	1,03 1,07 1,13 1,05 1,10 1,08 1,15	1,07 1,22 1,35 1,2 1,3 1,25 1,40

Отмечаем, что и для первой ступени основным критерием работоспособности является контактная, а не изгибная прочность. Далее выполняют проверочный расчет на перегрузку.

В результате получено: 1-я ступень—m_n=1,5 мм, z₁=26, z₂=157, d₁=40мм, d₂=240 мм, a₁=140 мм, β=11°21'40", b_wl=28 мм; 2-я ступень — т=2,5мм, z₁=37, z₂=123, d₁=92,5 мм, d₂=307,5, a₂=200мм, b_w2=80 мм.

П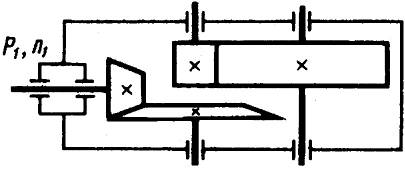 ример 3.3 В редукторе (пример 3.2) заменить первую косозубую цилиндрическую пару конической парой с круговыми зубьями (рис.3.13) [2]. Расчет выполнить только для конической пары.

Р

Рис.3.13

ешение. Принимаем для конической пары и₁=4. Материалы и термообработку колеса и шестерни сохраняем. При этом сохраняются и допускаемые напряжения: [σ_н]=625 МПа, [σ_F1]=363 МПа, [σ_F2]=246 МПа.

1. Принимаем К_bе=0,285.

При H₂≤350НВ принимаем (рис.3.14) К_Нβ=1, =1,3+0,13·4=1,65. При T₁=45·10³ Н мм находим T₂=45·10³·4·0,96=173·10³Н·мм.

Затем вычисляем

d'_e2=2,9 =177 мм;

=91,22 мм;

b'=K_beR'_e =0,285·91,22=26 мм.

2. Определяем геометрические параметры. Углы делительных конусов tgδ₂=u₁=4, δ₂=75°57'50" (вычисление с точностью до 10"), δ₁=14°2'10", d'_el=d'_e2/u=177/4=44,25 мм.

Далее расчет ведем по параметрам среднего сечения, в котором для круговых зубьев нормальный модуль принимают из стандартного ряда:

=44,25(91,22-0,5·26)/91,22=37,94 мм.

По графику рис. 3.15, =12 и, далее, z₁=l,3 =15,6.

Округляем до целого значения z₁=16, =37,94/16≈2,4.

Принимаем β_n=35°,

=1,966 мм.

Округляем до стандартного и принимаем m_nm=2 мм.

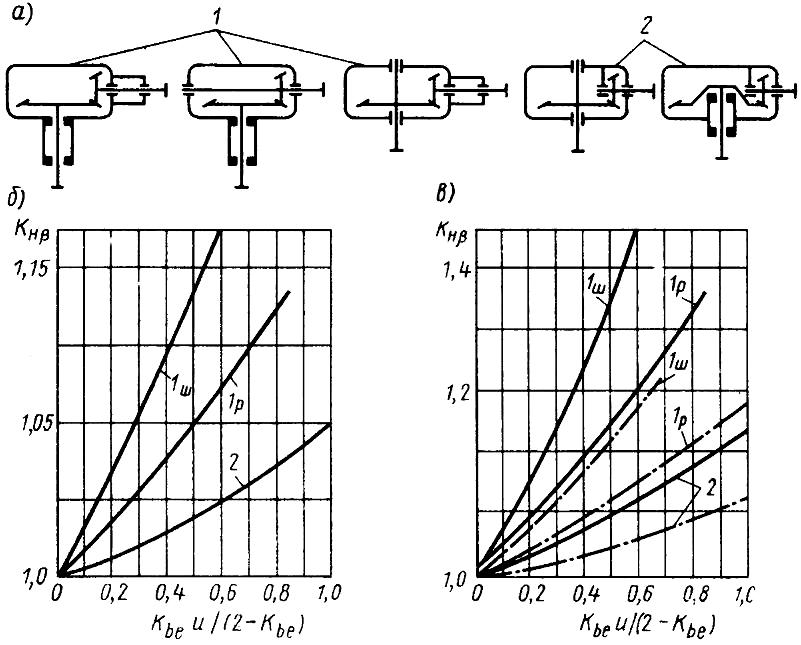
Рис.3.14

При этом m_tm=2/cos35°=2,422 мм. и z'₁ =37,94/2,442=15,54. Окончательно принимаем z₁=16, z₂=z₁·u=16·4=64.

Примечание. В нашем случае z₂—целое число. Если z₂ приходится округлять до целого числа, то изменится u₁. Тогда надо уточнять углы δ₁ и δ₂.

Далее

d_m1=m_tm z₁=2,442 16=39,072 мм;

d_m2= m_tm z₂=2,442·64=156,288 мм.

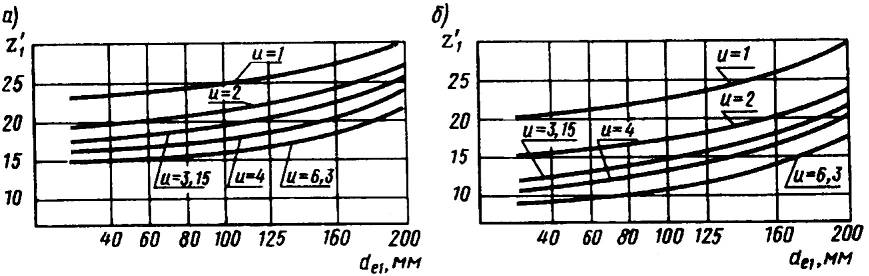
Рис. 3.15

3.Проверяем контактную прочность при α_w=α=20°. Предварительно определяем v=πd_mln₁60=π·39,072·10³·960/60≈2 м/с.

По табл. 3.13 назначаем 8-ю степень точности. По табл. 3.14 с понижением степени точности на одну степень находим K_Hv= ,04. При ранее найденном K_Hβ=1 получаем K_H=K_Hβ K_Hv=1,04.

Определяем напряжение

МПа<[σ_H]=625МПа.

Расхождение <5% условие прочности соблюдается. Окончательно принимаем b=26 мм.

Примечание. При существенных расхождениях корректируют значение b по условию b=b' (σ_H/[σ_H])².

4. Проверяем прочность по напряжениям изгиба. Предварительно находим

F_t=2T₁/d_ml=2·45·10³/39,072=2303 Н.

Назначаем коэффициенты смещения

0,36.

По формуле z_vn1=16/(0,97·0,819³)≈30: z_vn2=64/(0,24·0,819³)=385. По графику рис. 3.5 находим Y_FS1=3,68; Y_FS2=3,77. По табл. 3.14, с понижением степени точности на одну степень K_Fv=1,08. При ранее найденном значении K_Hβ=1 находим

K_Fβ =1+(K_Hβ-1)1,5=1 и K_F= K_FβK_Fv=1,08.

Вычисляем =0,85+0,043·4=1,022.

Сравниваем значения [ ]/Y_FS1=363/3,68=98,6 и [ ]/Y_FS2=246/3,77=65,3. Расчет ведем по колесу (меньшему значению). и находим =3,77·2303·1,08/(1,022·26·2)=176 МПа<[ ]=246 МПа.

Условие прочности соблюдаются. Основным критерием является прочность по контактным напряжениям.

Далее выполняют проверочный расчет на перегрузку по аналогии с п. 8 примера 3.1

5. Определяем другие геометрические параметры: R_m=d_m1(2sinδ₁)=39,072/(2·0,24254)=80,55 мм; R_е=R_m+0,5b=80,55+0,5·26=93,55 мм; d_e1=d_m1R_e/R_m=39,072·93,55/80155=45,38 мм; m_te=d_e1/z₁=45,5/16=2,836 мм; d_e2=m_te·z_e2=2,836·64=181,5 мм.

Ранее были найдены: m_nm=2 мм, z₁=16, z₂=64, b=26 мм, δ₁=14°2'10˝, δ₂=75°57'50".

Примечание. Остальные геометрические параметры (в том числе измерительный комплекс), которые не используют при расчетах на прочность, рассчитывают по ГОСТ 19624—74 с прямыми и по ГОСТ 19326—73 с круговыми зубьями.

Пример 3.4 Рассчитать передачу по схеме (см. рис. 3.16) при Р_а=25кВт, п_а=960 мин^-1, =5,5; нагрузка близка к постоянной, срок службы длительный [2].

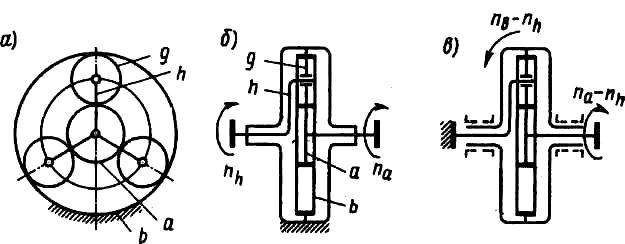
Рис. 3.16

Решение. 1. Принимаем число сателлитов С=3 и определяем числа зубьев. Выбираем z_a=21 и, по формуле (8.75),

z_b=( -l)z_a=(5,5- 1)21=94,5.

Принимаем, z_b=93 по условию симметричного размещения сателлитов. По условию (8.90)^*,

z_g=(z_b-z_a)/2=(93-21)/2=36.

По условию (8.91), (21+36)sin (π/3)>(36+2) или 49,4>38, т.е. условие соседства выполняется.

Действительное передаточное отношение

=l+z_b/z_a=1+93/21=5,44

отличается от заданного не более допускаемых±4%.

2. Определяем размеры колес пары а—g по контактной прочности—формула (8.88). Выбираем прямозубое зацепление. Назначаем (см. табл. 8.8) сталь 40Х при средней твердости для колеса а 280 НВ, а для сателлита g—250 НВ.

В конструкции предусматриваем плавающим центральное колесо и по рекомендации (8.81) принимаем Кс=1,15. Для рассматриваемой пары в формуле (8.88)

u=z_g/z_a=36/21=l,73; d₁=d_a; C=3.

Принимаем ψ_ba=0,5 [см. рекомендации—формула (8.89)].

По формуле (8.55) определяем допускаемые контактные напряжения; по табл. 8.9 для материала сателлита, как менее прочного, имеем =2НВ+70=2·250+70=570 МПа; s_H=1,1.

И далее, Z_N=l —длительно работающая передача, для которой N_HE>N_HG [см. формулу (8.61)]. При этом [σ_н]=570/1,1=520 МПа.

*Далее обозначение номеров формул, рис. и табл. принято по первоисточнику

По графику рис. 8.15 (кривая V), K_Hβ=1,02, Т₁=Т_a=(30/π)(P_a/n_a)=30·25·10³/(π·960)=250Н·м=250·10³ Н·мм.

Подставляя данные в формулу (8.88)

мм.

получаем b_w= =84·0,5=42 мм; m= =84/21=4 мм. По табл. 8.1 принимаем т=4мм. Уточняем: d_a=21·4=84 мм; d_a= 36·4=144 мм; d_b=93·4=372 мм; условие соседства: 49,4>44.

3.Выполняем проверочный расчет на усталость по контактным напряжениям— формула (8.10) при α_w=α=20°.

Окружная скорость v=πd_an_a/60 =π·8410^-3·960/60=4,2 м/с. По табл. 8.2 назначаем 8-ю степень точности. По табл. 8.3, K_Hv≈1,2 и, далее, K_H=K_HβK_Hv= 1,02·1,2=1,22.

По формуле (8.10) с учетом Кс и С имеем

МПа≈ =520 МПа.

4.Выполняем проверочный расчет по напряжениям изгиба — формула (8.19).

Рассчитываем зубья сателлита, так как они подвергаются знакопеременным напряжениям.

По табл. (8.9),. =1,8HB=1,8·250=450 МПа.

По формуле (8.67), принимая S_F=1,75, Y_N=1 и Y_A=0,7, находим =450·0,7/1,75=180 МПа.

По графику рис. 8.18, при х=0 Y_FS= ,8. По графику рис. 8.15 (кривая V), K_Fβ= l,05. По табл. 8.3, K_Fv=1,4 и, далее, K_F=1,05·1,4=1,47.

По формуле (8.80),

F_t=F_ta=2·250·10³·1,15/(84·3)=2282Н.

По формуле (8.19),

σ_F=3,8·2282·1,47/(42·4)=76 МПа<[σ_F]=180 МПа. Условие прочности соблюдается.

5. Все размеры второй пары (сателлит g — колесо b) известны. Поэтому расчет выполняют в форме проверочного на контактную и изгибную прочность.

Методика расчета та же, что и для первой пары. Особенности расчета указаны выше.

Пример 3.5. В передаче из примера 8.1 (см. рис. 3.8) заменить эвольвентное зацепление второй ступени зацеплением Новикова и сравнить размеры [2].

Решение. Материал и допускаемые напряжения сохраняем: [σ_H]=500 МПа; для шестерни [σ_F]=278МПа; u=3,34; T₁=262·10³ Н·мм, n₁=160 мин^-1.

1. Определяем d₁ по формуле (8.95). По рекомендациям (см. выше) предварительно назначаем β=14°, ε_β=1,3, z₁=15. По графику рис. 8.55 находим Кв=0,14. По табл. 8.3, учитывая, что 2-я ступень тихоходная, принимаем К_Нv=1,05. Подставляя данные в формулу (8.95), с учетом ε'_β=1 находим

мм.

Модуль m_n=d₁cosβ/z₁=54·0,97/15=3,49 мм. По табл. 8.1 принимаем m_n=3,5 мм. При этом d₁=3,5·15/0,97=54,12 мм.

2. По формуле (8.96) проверяем прочность по напряжениям изгиба. Предварительно принимаем K_Fv=K_Hv=1,05; по рис. 8.55 К_и≈0,2 и при =0,3, ψ=1,25. Далее z_v1=z₁/cos³β=15/0,9135=16,5 и Y_F ≈0,95. При этом

МПа<[σ_F]=278 МПа

Условия прочности соблюдаются. Отмечаем, что в нашем примере нагрузка ограничивается контактной прочностью.

3. Определяем ширину колес по формуле (8.92): b_w= ε_β πm_n/sinβ=l,3π3,5/sinl4°≈59 мм. Число зубьев колеса z₂=z₁u=15·3,34≈50. Диаметр колеса d₂=z₂m_n/cosβ=50·3,5/cosl4°=180,4 мм.

В заключение сравниваем передачи:

передача Новикова передача эвольвентная

d₁=54,12 мм 90 мм

d₂=180,4 мм 300 мм

b_w=59мм 86 мм

Отмечаем существенное уменьшение габаритов.