1.5.3 Примеры частных видов функций Ляпунова

1. Пусть дана

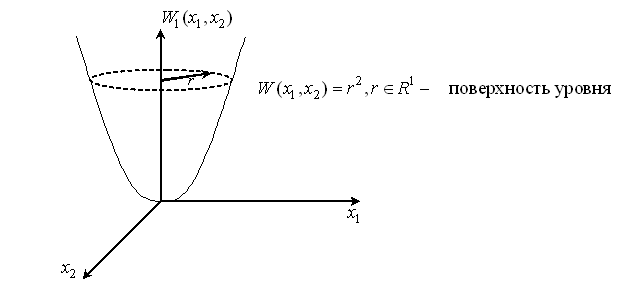
Рисунок 3

.

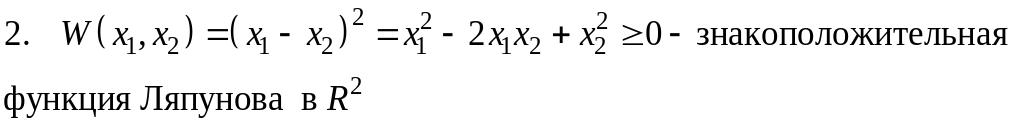
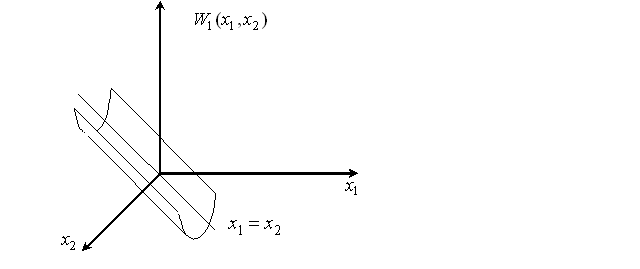
Рисунок 4

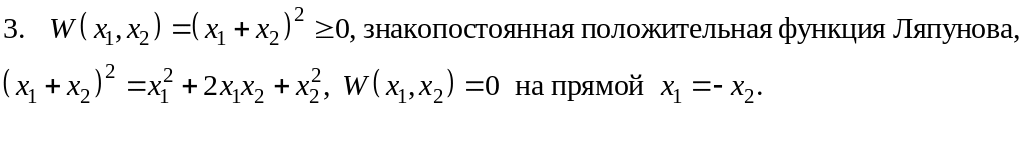
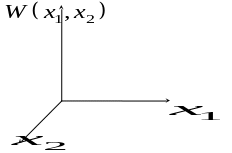
Рисунок 5

Утверждение. Отметим, что в примерах (1)÷(3) построенные функции Ляпунова определялись следующими матрицами:

1.

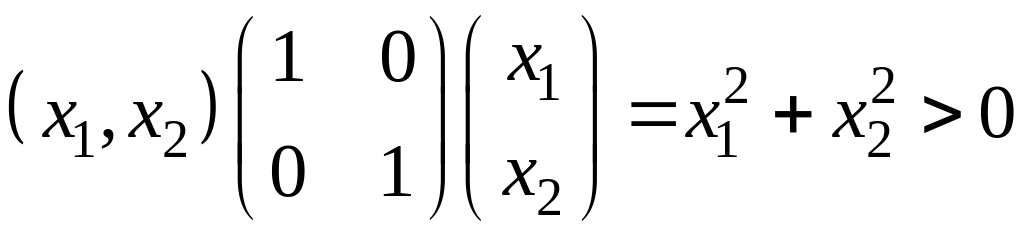
2.

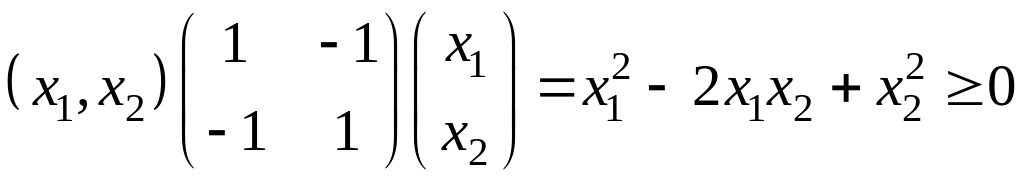
3. _■

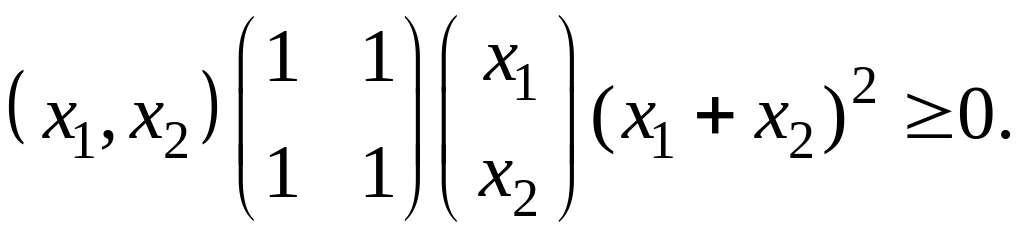5.

Допускает БМВП при (знакопостоянная положительная).

6.

Ограничена, знакопостоянная положительная; но не равномерно по t, следовательно, не допускает БМВП при

7. Положительно определенная; не допускает БМВП при

8. . Положительно определенная внутри шара единичного радиуса, допускает БМВП при

1.6 Полная производная по времени t функции Ляпунова, вычисленная в силу системы

Пусть дана нелинейная нестационарная система дифференциальных уравнений вида:

(1.6.1)

с областью определения

(1.6.2)

П ричем в этой области функция :

(а) ) непрерывна по t, x;

(б) имеет непрерывные частные производные вида , (1.1.4) ограниченные равномерно по на любом компактном подмно-

жестве из области (или говорят кратко, непрерывно

дифференцируемы по );

в) , т.е. система допускает тривиальное решение

Условия (1.6.3) означают, что область (1.6.2) есть область единственности для системы (1.6.1).

Пусть также дана функция Ляпунова вида , определенная в некоторой области , и пусть функция Ляпунова вида – непрерывно дифференцируема по t, x в , т.е. усиливаем свойства ее непрерывности, задаваемыми введенным выше определением функции Ляпунова.

Вычислим полную производную по времени как сложную функцию аргументов t, x. Введем обозначения

Тогда

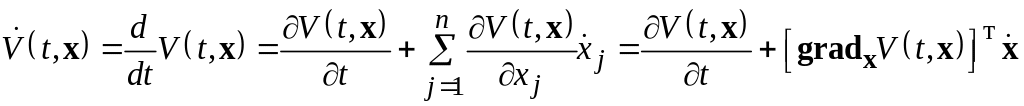
Подставляя в последнее выражение для в силу системы (1.6.1), получим:

(1.6.4)

Здесь введена вектор-функция – градиент скалярной-функции по вектору x вида:

(1.6.5)

Определение. Выражение (1.6.4) называется полной производной по времени t функции Ляпунова , вычисленной в силу приведенной системы (1.6.1).■

Замечание 1. Если есть произвольное решение системы (1.6.1), то , в силу выражения (1.6.4), представляет собой полную производную по времени t сложной функции , т.е.

.■ (1.6.6)

Замечание 2. Заметим, что если функции Ляпунова из формулы полной производной (1.6.4) не придать дополнительные свойства непрерывной дифференцируемости по t и x , то из формулы (1.6.6) могут не следовать формулы (1.6.4), (1.6.5), так как для ) не будет удовлетворяться требование непрерывности по t , x к ней как к функции Ляпунова. ■

1.7 Геометрический смысл полной производной по времени функции Ляпунова, вычисленной в силу приведенной системы

Пусть (для определенности) дана положительно определенная функция Ляпунова . Знание ее производной в силу системы (1.6.1) позволяет наглядно выяснить характер движения изображающей точки вдоль интегральной кривой (решения) системы.

Действительно, пусть в некоторый фиксированный момент времени изображающая точка М занимает некоторое положение на кривой решение системы (1.6.1). Построим поверхность (с – положительное число), проходящее через точку М. Затем по формуле (1.6.4) вычислим полную производную функции V в этой точке. Так как , и будет равна скалярному произведению вектор-функций

(1.7.1)

причем напомним, что вектор-функция f определяет вектор скорости движения изображающей точки вдоль решения системы. Рассмотрим три возможных случая. Рассмотрим рисунок 6.

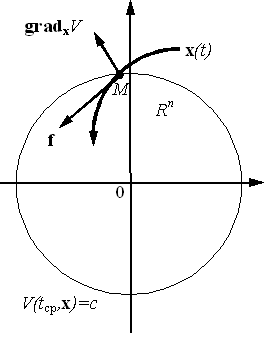
Рисунок 6,а

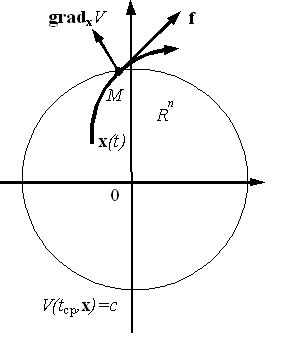
Рисунок 6,б

1. Пусть в данном положении точки М производная отрицательна

т.е. функция V убывает на решении системы (см. рисунок 6,а).

Известно, что вектор направлен по нормали к поверхности в точке М в сторону возрастания функции V, т.е.во внешнюю часть поверхности V=с, если функция Ляпунова V положительно определенная (и внутрь поверхности , если V отрицательно определенная), а вектор-функция f скорости движения точки М касателен к поверхности в точке М.

Таким образом, отрицательность - скалярного произведения (1.7.1) векторов означает, что угол между ними тупой, и так как вектор направлен по внешней нормами к поверхности в точке М , то вектор скорости f точки М направлен внутрь этой поверхности. А это означает, что траектория изображающей точки М (интегральная кривая, решение системы) пересекает поверхность снаружи вовнутрь (см. рисунок 6,а).

2. Пусть в данном положении точки М , т.е. функция V возрастает на решении системы (см. рисунок 6,б). Отрицательность - скалярного произведения (1.7.1) векторов означает, что угол между ними острый, и, следовательно, траектория изображающей точки М пересекает поверхность изнутри наружу (см. рисунок 6,б).

3. Пусть в данном положении точки М производная , т.е. скалярное произведение векторов равно нулю, угол между этими векторами - прямой, и следовательно, траектория изображающей точки М касается поверхности (в частности, она может целиком лежать на этой поверхности).

Замечание. Главный идейный смысл второго, или, как его еще называют, прямого метода Ляпунова, состоит в том, что свойства устойчивости тривиального решения приведенной по Ляпунову системы, или, что то же, системы возмущенного движения, изучаются по поведению полной производной по времени функции Ляпунова, вычисленной в силу системы (говорят, вдоль решений системы уравнений возмущенного движения), причем сами решения остаются неизвестными, а их производные заменяются известными правыми частями , т.е. второй метод Ляпунова является косвенным методом исследования свойств устойчивости решений приведенной системы. ■