1. Закон всемирного тяготения.

Гравитационным полем называют силовое поле, в котором ускорения пробных частиц за счет сил со стороны поля, не зависят от массы частиц. Гравитационное поле обеспечивает гравитационное взаимодействие, в котором участвуют все объекты материального мира.

Закон всемирного тяготения – закон, описывающий гравитационное взаимодействие материальных точек.

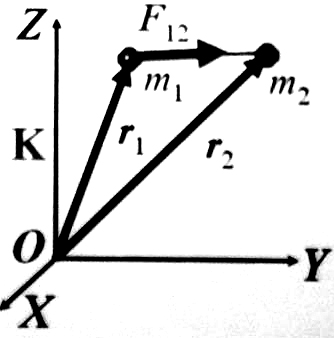
Где G=6.673*10^-8 см³/г*с² – гравитационная постоянная, m₁ m₂ – гравитационные массы тел.

В силу симметрии закона, он справедлив и для тел, обладающих сферической симметрией – в частности, для планет солнечной системы.

2. Принцип эквивалентности.

Рассмотрим гравитационное взаимодействие точечного тела с Землей.

Сила, действующая на тело со стороны Земли – сила тяжести.

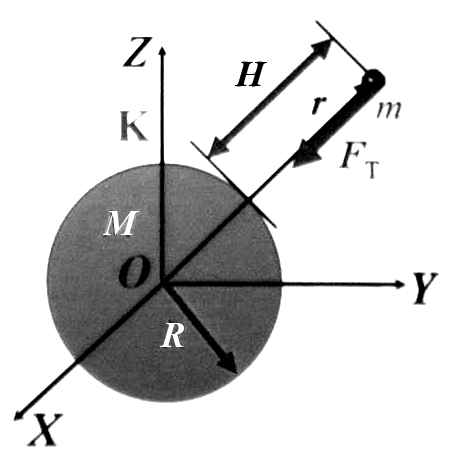
Где R=6.371*10⁸ см – радиус Земли

M=5.977*10²⁷ г – масса Земли

Под действием силы тяжести тело приобретает ускорение:

– инертная масса тела

Принцип эквивалентности утверждает, что гравитационная и инертная массы тела численно всегда совпадают.

Следовательно, где – ускорение свободного падения.

3. Законы Кеплера (1 и 2 законы).

Гравитационное поле потенциально и его потенциальная функция имеет вид:

П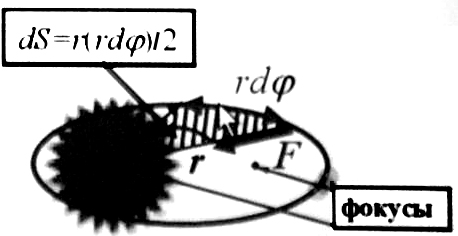 отенциальное поле, потенциальная функция которого , называют центральным полем.

1 Закон Кеплера:

Единственной замкнутой траекторией пробной частицы в центральном поле (вида 1) является эллипс (с источником поля в фокусе).

2 Закон Кеплера:

При движении в центральном поле

С другой стороны

Таким образом, следовательно, за равные промежутки времени радиус-вектор частицы описывает равные площади.

4. Законы Кеплера (3 закон).

Для задачи Кеплера рассмотрим центральное поле вида

₍₁₎

где – произвольная постоянная и

Если сделать замены:

то:

• скорость

• кинетическая энергия

• потенциальная энергия

• полная механическая энергия

Следовательно, или . Это означает, что в центральном поле вида (1) уравнения движения допускают геометрически подобные траектории, причем:

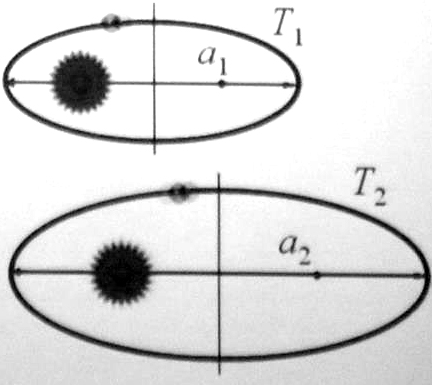(К)

где и – промежутки времени, и – линейные размеры двух траекторий.

Для гравитационного поля, т. е. центрального поля вида (1), соотношение (К) можно записать так (в этом случае ):

Квадраты периодов обращения пробных частиц в гравитационном поле относятся как кубы больших полуосей их орбит.

5. Неинерциальные системы отсчёта.

В ИСО законом динамики является 2 закон Ньютона. Возникает вопрос: как записать закон динамики для частицы в неинерциальной СО (НСО) K’, движущейся относительно ИСО K с известным ускорением ?

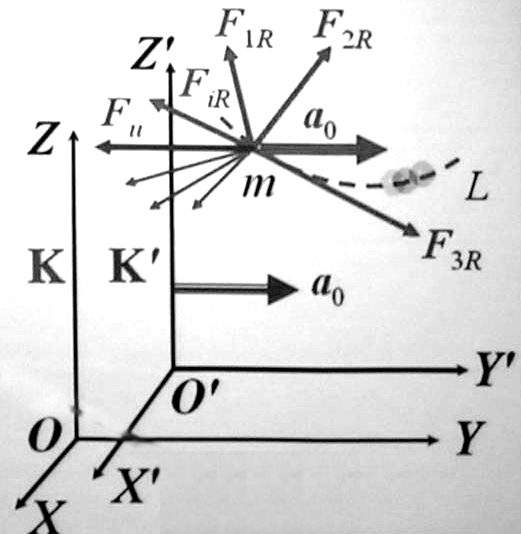
Рассмотрим движение некоторой материальной точки массой из двух СО – ИСО K и НСО K’. Величину и направление ускорения НСО выберем равным ускорению частицы (относительно ИСО К). Следовательно, в НСО K’ ускорение частицы равно нулю и закон динамики должен иметь вид:

Закон динамики в ИСО K:

где реальные силы, действующие на частицу. Введем обозначение:

Величину рассматривают как дополнительную (фиктивную) силу, возникающую в НСО, и называют силой инерции. Тогда:

6. Сила тяжести и вес тела.

Рассмотрим небольшое тело, подвешенное на некоторой высоте от поверхности Земли. Земля вращается (суточное вращение) – вместе с ней в этом вращении участвуют все тела на Земле. За счет гравитационного взаимодействия тела с Землей, на тело действует сила тяжести.

В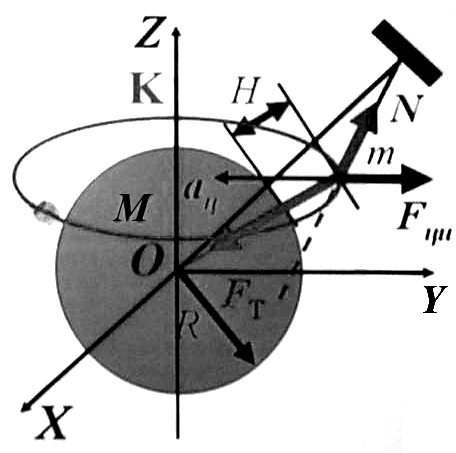 ИСО K, связанной с центром Земли, закон динамики для нашей частицы имеет вид:

где – сила реакции нити, – центростремительное ускорение. Поверхность Земли является НСО, вращающейся с ускорением .

Закон динамики для такой неинерциальной системы отсчета принимает вид:

где – центробежная сила инерции.

Весом тела называют силу, действующую на горизонтальную опору или вертикальный подвес.

Следовательно, вес тела массой :

Тогда, учитывая, что:

где – радиус окружности, по которой движется частица вместе с Землей, получим:

Введем обозначение:

Таким образом, вес тела массой :

где – ускорение свободного падения на широте, на которой расположена частица

Сила тяжести – сила, действующая на тело со стороны Земли.

7. Промежутки времени в различных ИСО.

_{Рассмотрим две ИСО, движущиеся вдоль осей X:}

_{Так как (интервал – дополнительный постулат СТО), то:}

_{Время в системе покоя называют собственным и обозначают (у нас ). Время во всех остальных ИСО называют мировым и обозначают .}

_{где – релятивистский фактор (Лоренц-фактор):}

_{Промежутки времени по собственным часам всегда минимальны.}

8. Длина отрезков в различных ИСО.

Р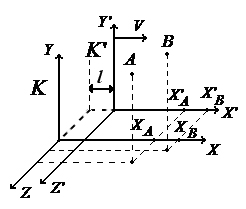 ассмотрим две ИСО, движущиеся вдоль осей X:

– длина стержня в той системе, где он находится в состоянии покоя (в данном случае в ИСО K’). Время в системе, где часы находятся в покое, является собственным:

Тогда:

_{где – релятивистский фактор (Лоренц-фактор):}

Длина стержня в системе покоя (собственная длина) всегда максимальна.

9. Преобразование Лоренца.

Р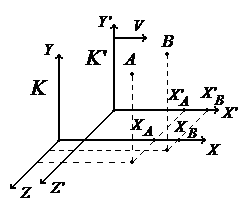 ассмотрим событие из ИСО K и K’

При измерениях из ИСО K’:

При измерениях из ИСО K:

Преобразования Лоренца при переходе от K к K’ имеют вид:

При обратном переходе:

Преобразования Лоренца при переходят в преобразования Галилея.

10. Закон сложения скоростей в СТО.

Рассмотрим произвольно движущуюся материальную точку из двух ИСО K и K’. По определению:

Следовательно, нам нужно найти связь:

Это закон сложения скоростей для компоненты скорости точки вдоль скорости ИСО K’

Закон сложения скоростей для нормальных компонент скорости.

11. Относительность понятия одновременности

Рассмотрим два события A и B из двух ИСО K и K’:

Найдем промежуток времени между событиями:

(R7)

где обозначено

Пусть события A и B одновременны с точки зрения наблюдателя из ИСО K (т. е. ), тогда для наблюдателя из ИСО K’:

События, одновременные в одной ИСО, во всех остальных ИСО не одновременны. Принцип причинности никогда не нарушается.

12. Основные динамические характеристики (понятие силы в СТО, масса и энергия в СТО, масса покоя системы частиц)

Понятие силы в СТО:

В классической механике сила определяется законом Ньютона:

где – импульс:

В СТО определение силы остается без изменений:

(D1)

Определение импульса уточняется с учетом зависимости промежутков времени от ИСО – производная берется по собственному времени:

(D2)

Масса и энергия в СТО:

В классической механике вводится элементарное изменение кинетической энергии:

В СТО это определение остается без изменений (для импульса используется определение D2):

Интегрируя формулу D3, для кинетической энергии свободной частицы получим:

(D4)

Величину:

(D5)

называют полной механической энергией свободной частицы. Для покоящейся частицы:

Величину называют энергией покоя. С обозначением для релятивистской массы, определение импульса D2 принимает вид:

(D6)

Из формул D5-D6 можно получить связь между импульсом и полной механической энергией свободной частицы:

(D7)

Из этой формулы следует, что масса покоя в СТО становится неаддитивной величиной – сумма масс отдельных частиц системы не равна массе системы.

Масса покоя частиц системы:

Для энергии и импульса системы из двух частиц, очевидно, можно записать

Возведем эти уравнения в квадрат

и подставим в формулу

Получим

Преобразуем это выражение

Отсюда следует

(D8)

Это масса покоя системы из двух частиц.

Где введены обозначения

Для того, чтобы убедиться, что воспользуемся введенными обозначениями, получим

Введем еще одно обозначение , тогда

, которое выполняется безусловно,

то есть

Таким образом, масса системы частиц равна сумме масс отдельных частиц только в том случае, когда все частицы системы находятся в покое или движутся равномерно прямолинейно в одном направлении – условия невыполнимые ни для одной реальной системы.

Этот результат является одним из важнейших практических выводов СТО.

13. Уравнения движения в СТО

(D1), (D2)

Согласно уравнениям D1-D2, уравнения движения частиц имеют вид:

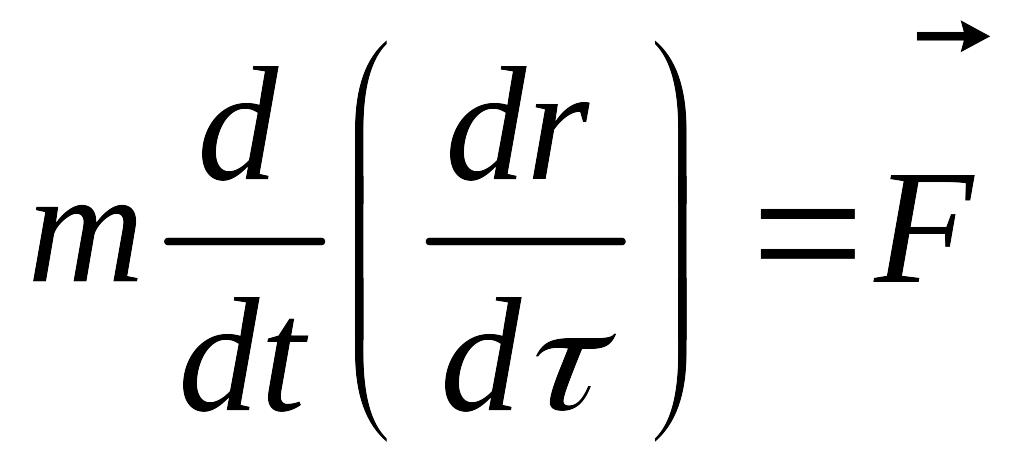(D9)

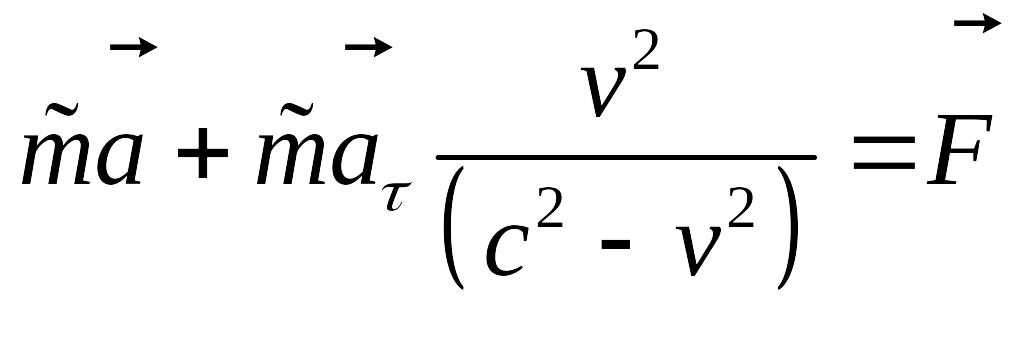
где – тангенциальное ускорение.

Таким образом, сила в общем случае не является причиной ускорения, как это было в классической механике – т. е. сила не является линейной функцией ускорения.

Частные случаи:

Частица движется прямолинейно:

В этом случае и мы получаем

Частица движется по окружности:

В этом случае и мы получаем

14. Термодинамическая система

Термодинамической системой называют любой макроскопический объект, который обменивается энергией с любыми объектами окружающего мира. Термодинамическая система – это математическая абстракция реального тела Природы.

Для описания состояний термодинамической системы используют термодинамические параметры: и т. д.

Соответственно, термодинамической системой (ТС) будем называть любой воображаемый объем пространства, которому приписаны все ТП данного тела.