2. Построение структурной модели электропривода

Для проведения динамического анализа построим структурную модель функционального уровня электропривода механизма главного движения. В соответствии с функциональной схемой электропривода (рис. 9.1) модель будет содержать следующие функциональные блоки:

• асинхронный электродвигатель;

• преобразователь частоты (автономный инвертор напряжения);

• регуляторы;

• координатные преобразователи, блоки развязки и т.п.

Расчетные параметры электродвигателя 4А132S6У3 и механизма главного движения, который будем представлять абсолютно жесткой механической частью, представлены в табл. 9.1.

Таблица 9.1 .

Динамические параметры объекта управления

Наименование	Обозначение	Величина
Электродвигатель 4А132S6У3
Номинальное напряжение	Uн	220 В
Номинальный ток	Iн	12.2549 А
Номинальный момент	Мн	54.3135 Нм
Перегрузочная способность по моменту		2.5
Номинальная скорость вращения	nн	967 об/мин
	н	101.257 1/с
Сопротивление фазы статора	R1	1.1604 Ом
Сопротивление фазы ротора	R2	0.6850 Ом
Индуктивность фазы статора	L1	0.1125 Гн
Индуктивность фазы ротора	L2	0.1144 Гн
Взаимная индуктивность	L12	0.1086 Гн
Коэффициент усиления преобразователя частоты	kПЧ	100
Механическая часть
Приведенный момент инерции системы электропривода	JS	0.82 кг*м2

1. Структурная модель электродвигателя

Для построения структурной модели электродвигателя будем использовать исходное математическое описание, представленное в главе 9 в виде уравнений (9.1) – (9.6). После приведения уравнений к виду, удобному для построения структурной модели уравнения принимают вид:

(9.1)

где (9.2)

Приведенные выше уравнения графически представим в виде функциональных блоков AD_DQ_F2, EMP_QD_F2, Moment_F2, внешнее и внутренне представление которых приведены на рис. 9.1 – 9.4.

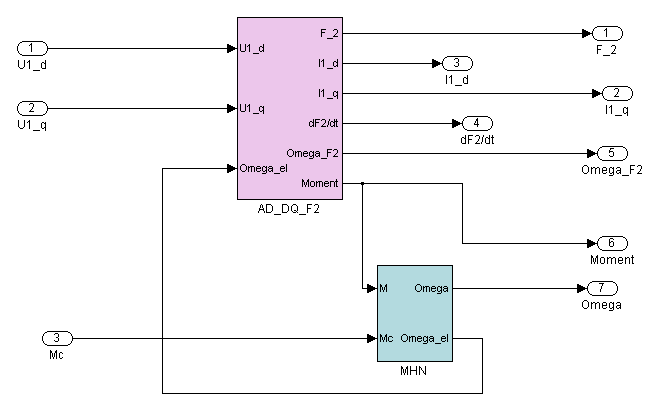
Рис. 9.1 Внутреннее представление функционального блока AD_MHN_F2

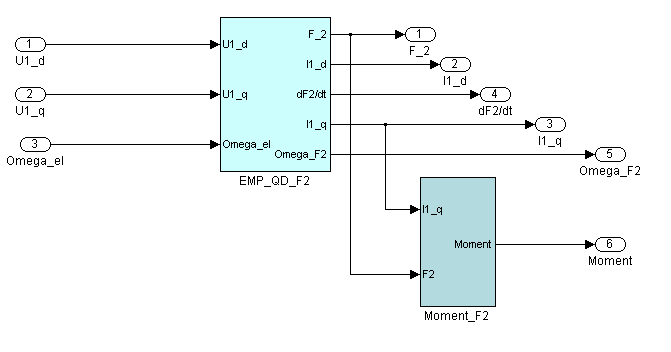
Рис. 9.2. Внутреннее представление функционального блока AD_DQ_F2

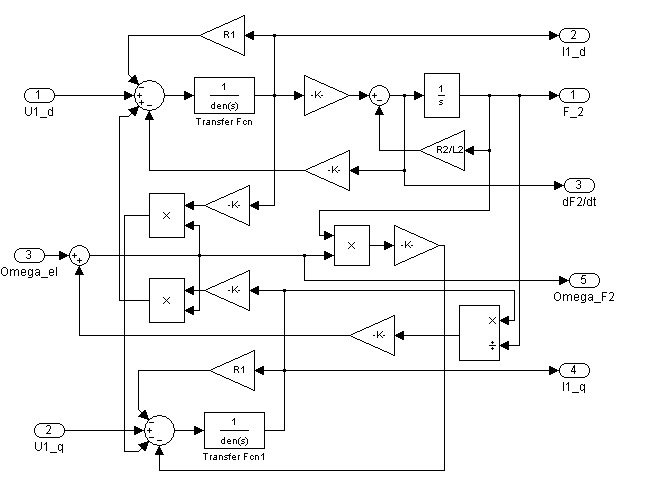
Рис. 9.3. Внутреннее представление функционального блока EMP_QD_F2

Рис. 9.4. Внутреннее представление функционального блока Moment_F2

Механическую часть электропривода представим в виде функционального блока МНN (рис. 9.1., 9.5).

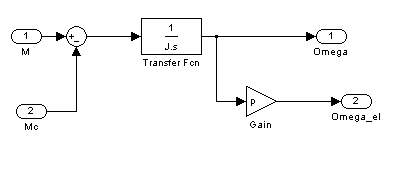
Рис. 9.5. Внутреннее представление функционального блока MHN

2. Определение номинальных значений потока сцепления ротора и реактивной составляющей тока статора

Для построения структурной модели электропривода в целом необходимо рассчитать номинальные значения потокосцепления ротора ₂, реактивной составляющей тока статора I_d и ЕДС ротора. Для получения этих значений выполним имитационный эксперимент прямого пуска электродвигателя при номинальных значениях напряжения и частоты сети, момента статического сопротивления.

Схема модели для этого эксперимента приведена на рис. 9.6. Там же в экранах соответствующих дисплеев можно прочитать значения необходимых координат

Динамические характеристики прямого пуска приведены на рис. 9.7.

Реактивную составляющую тока статора определим по формуле (9.18):

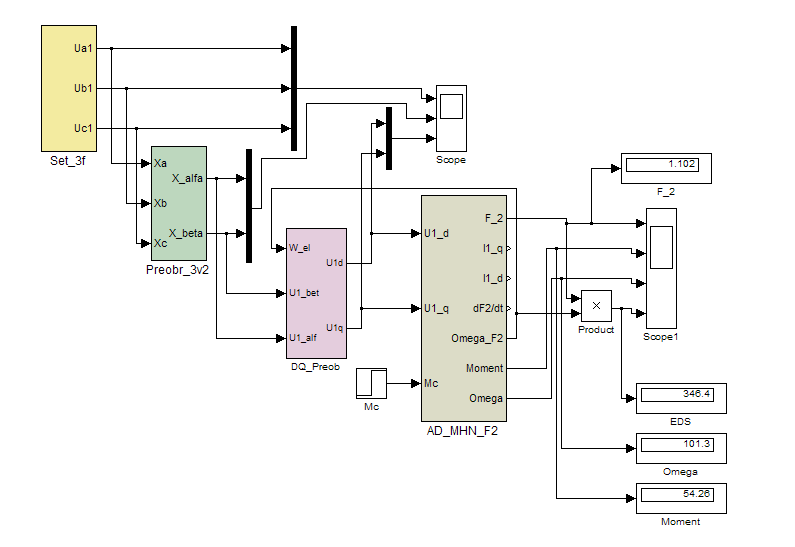
Рис. 9.6. Структурная модель прямого пуска электродвигателя от сети

Рис. 9.7. Динамические характеристики прямого пуска АД от сети