8 Контрольные вопросы

1. Какие существуют режимы течения жидкости, в чем их отличие?

2. Что характеризуют верхняя и нижняя критические скорости движения жидкости?

3. Какое критическое число Рейнольдса принимают в переходной области?

4. Как определяется число Рейнольдса?

5. Как зависит число Рейнольдса от температуры и физических свойств исследуемой жидкости?

6. В каком порядке проводятся экспериментальные исследования на стенде?

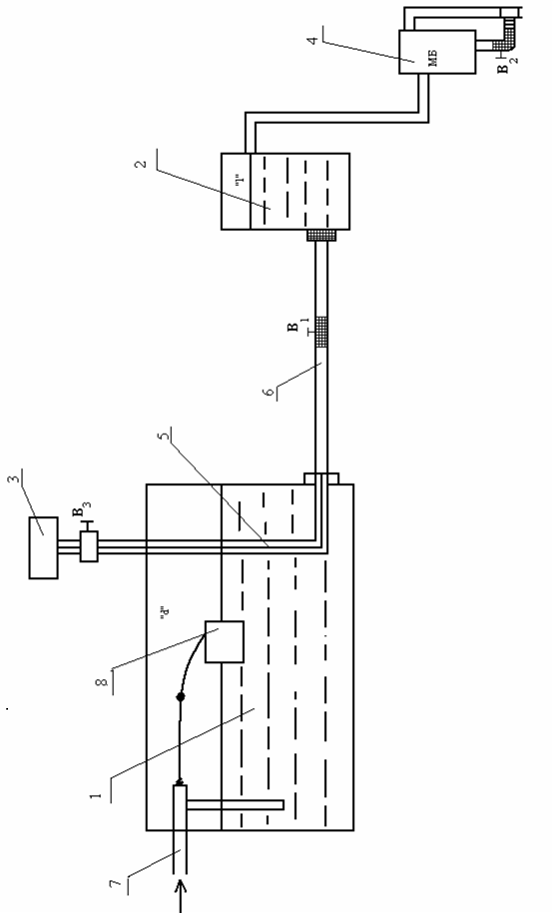
Лабораторная работа № 4

Экспериментальная проверка уравнения бернулли

1 Цель работы

Построить пьезометрическую линию и линию полного напора на основе уравнения Бернулли при движении реальной жидкости в трубопроводе переменного сечения.

2 Содержание работы

- установить взаимосвязь между основными параметрами (давление, скорость) потока движущейся жидкости;

- изучить геометрический и энергетический смысл уравнения Бернулли для элементарной струйки идеальной и реальной жидкости;

- разобрать графическую иллюстрацию уравнения Бернулли для реального потока;

-ознакомиться с методикой экспериментального определения параметров движущейся жидкости.

3 Порядок выполнения работы

- изучить содержание методического указания и теоретический материал, связанные с данной работой;

- ответить на контрольные вопросы;

- ознакомиться со стендом и порядком проведения лабораторной работы;

- провести эксперименты;

- обработать результаты исследований и представить в виде графиков и таблиц;

- оформить и защитить отчет по данной работе.

4 Оборудование для работы

Лабораторный стенд и методические указания.

5 Теоретическая часть

5.1 Уравнение Бернулли для элементарной струйки идеальной жидкости

Уравнение Бернулли, устанавливающее связь между давлением и скоростью в движущемся потоке жидкости, является основным уравнением гидравлики. Написанное для двух произвольных сечений элементарной струйки идеальной жидкости уравнение Бернулли имеет вид:

. (4.1)

Координата z [м], определяет высоту положения частицы над какой-то плоскостью сравнения, называемой нивелирной высотой, или геометрическим напором, и определяет запас потенциальной энергии, обусловленный положением частицы (удельная потенциальная энергия положения).

Величина , представляющая высоту столба жидкости, уравновешивающего действующее в данной точке давление, называется пьезометрической высотой или пьезометрическим напором, и определяет запас потенциальной энергии, обусловленной давлением (удельная потенциальная энергия давления).

Суммой этих двух величин z + P/γ, называемой статической высотой или статическим напором, определяется полный запас потенциальной энергии 1 Н жидкости относительно принятой плоскости сравнения.

Величина v²/2g [м] представляет собой высоту столба жидкости, эквивалентную часть статического напора, под действием которого происходит движение жидкости. Эта величина, называемая динамическим, или скоростным напором, представляет собой удельную кинетическую энергию, т.е. кинетическую энергию, отнесенную к 1Н жидкости:

.

Уравнение Бернулли показывает, что при установившемся движении идеальной жидкости сумма геометрического, пьезометрического и динамического напоров в каждом поперечном сечении элементарной струйки есть величина постоянная, т.е.

.

Физический смысл этого уравнения заключается в том, что суммарная (полная) удельная энергия элементарной струйки идеальной жидкости при установившемся движении, состоящая из удельной потенциальной и удельной кинетической энергии, остается неизменной.