7 Содержание отчета

- цель и содержание работы;

- схема испытательного стенда;

- порядок проведения опытов и обработки экспериментальных данных (включая журнал измерений и вычислений);

- краткие выводы.

8 Контрольные вопросы

1. Какие потери энергии называют местными? По каким формулам они определяются?

2. Какие элементы трубопроводов (гидравлической аппаратуры) относятся к местным гидравлическим сопротивлениям?

3. Чем обусловлены потери гидравлической энергии при движении жидкости через внезапное и постепенное: расширение трубопровода, сужение трубопровода, поворот?

4. Определить расчетным путем коэффициент местного сопротивления для внезапного расширения (сужения).

5. Как определить потери гидравлической энергии в местном сопротивлении экспериментальным путем?

6. В чем отличие расчетных формул при определении коэффициента местного сопротивления для внезапного и постепенного сужения (внезапного и постепенного расширения)?

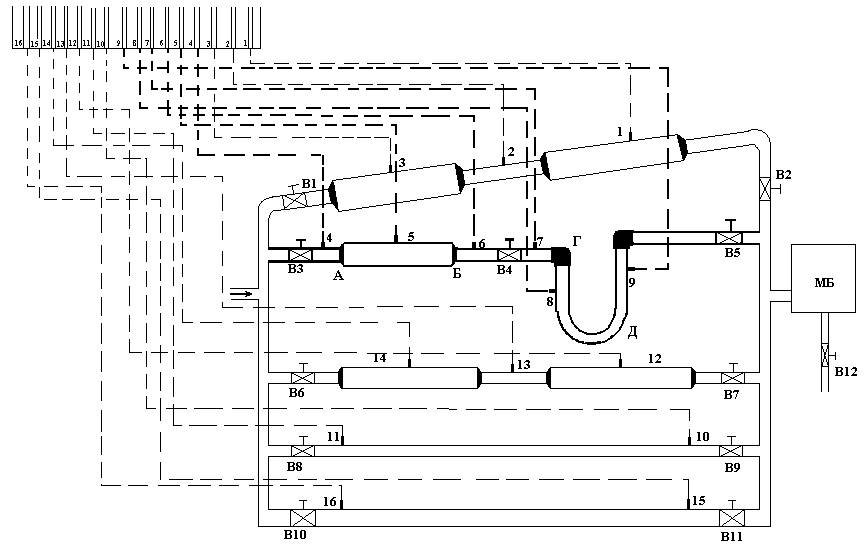
Рисунок 1.8. Схема лабораторного стенда

Таблица 1.2. Результаты измерений и расчетной обработки данных

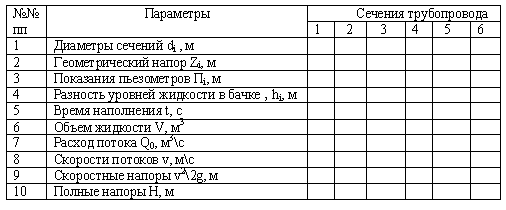
Таблица 1.3. Результаты расчета коэффициентов местных сопротивлений

Лабораторная работа № 2

Определение коэффициента гидравлического сопротивления в трубе

1 Цель работы

Экспериментальное определение коэффициента гидравлического сопротивления по длине трубопровода и коэффициента шероховатос­ти.

2 Содержание работы

- выявить основные факторы, влияющие на потери удельной гидравлической энергии по длине трубопровода;

- установить взаимосвязь между коэффициентом гидравличес­кого сопротивления, числом Рейнольдса, относительной шероховатостью и диаметром трубопровода;

- определить потери удельной гидравлической энергии при ламинарном и турбулентном режимах движения жидкости в трубопроводах;

- ознакомиться с методикой экспериментального определения коэффициента гидравлического сопротивления по длине трубопровода и коэффициента шероховатости.

3 Порядок выполнения работы

- изучить содержание методического указания и теоретический материал, связанные с данной работой;

- ответить на контрольные вопросы;

- ознакомиться с испытательным стендом и порядком проведения лабораторной работы;

- провести эксперименты;

- обработать результаты исследований и представить в виде графиков или таблиц;

- оформить и защитить отчет по лабораторной работе.

4 Оборудование для работы

Лабораторный испытательный стенд и методические указания.

5 Теоретическая часть

Потери на трение или потери по длине – это потери энергии, которые возникают в прямых трубах постоянного сечения при равномерном течении и возрастают пропорционально длине трубы. Этот вид потерь обусловлен внутренним трением в жидкости и трением о стенки трубопровода.

Потери напора по длине трубопровода, как показали опыты, зависят от средней скорости движения жидкости v, линейного размера живого сечения (диаметр d, гидравлический радиус R_г и др.), вязкости μ, плотности ρ, шероховатости стенок, выраженной средним размером выступов ∆ и длины трубопровода l.

Функционально это зависимость имеет вид

h_тр = f(v, d, μ, ρ, ∆, l).

Потерю напора можно выразить по общей формуле для гидравлических потерь

h_тр = ξ_трv²/2g, (2.1)

Однако, для определения потерь напора в круглой цилиндрической трубе удобнее коэффициент ξ_тр связать с относительной длиной трубы l/d

.

В результате формула (2.1) примет вид

(2.2)

или в единицах давления

, (2.3)

где γ – удельный вес жидкости.

Зависимость (2.2) называется формулой Дарси-Вейсбаха.

Безразмерный коэффициент λ называется коэффициентом потерь на трение или коэффициентом сопротивления трению.

Его можно рассматривать как коэффициент пропорциональности между потерей напора на трение с одной стороны, и произведением относительной длины трубы на скоростной напор с другой стороны.

П

Рисунок 2.1. Гидравлически гладкие и шероховатые трубы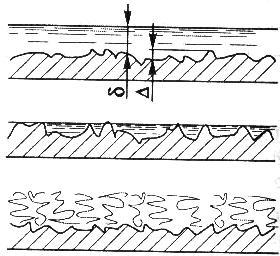

оверхности стенок труб (каналов) имеют ту или иную шероховатость. Обозначим высоту выступов шероховатости буквой ∆. Обычно ∆ называют абсолютной шероховатостью, а ее отношение к радиусу трубы (∆/r = 2∆/d) – относительной шероховатостью. Величина, обратная шероховатости называется относительной гладкостью (r/∆). С целью упрощения расчетов вводят понятие эквивалентной шероховатости ∆_экв, при которой потери напора в трубопроводе получаются такими же, как и при фактической неоднородной шероховатости.

При турбулентном режиме в зависимости от соотношения толщины ламинарного слоя δ и абсолютной шероховатости ∆ различают гидравлически гладкие и шероховатые трубопроводы (рисунок 2.1). Если ламинарный слой полностью закрывает выступы и неровности на стенках трубы (δ>∆), трубопровод считается гидравлически гладким. Если же δ<∆, то трубопровод считается гидравлически шероховатым.

Таблица 2.1. Значение ∆_экв для трубопроводов различного назначения

№ п/п	Материал и вид трубы	Состояние трубы	Значение ∆э 10-3, м
1	Тянутые трубы из стекла и цветных металлов	Новые, технически гладкие	0.000-0.002
2	Бесшовные стальные трубы	Новые и чистые После нескольких лет в эксплуатации	- 0.02 0.15 – 0.3
3	Стальные трубы сварные	Новые и чистые Умеренно заржавевшие Сильно заржавевшие или с большими отложениями Старые заржавевшие	0.03 – 0.1 0.3 – 0.7 2.0 – 4.0 0.8 – 1.5
4	Чугунные трубы	Новые Бывшие в употреблении Очень старые	0.3 - 0.4 0.5 – 1.5 до 30
5	Пластмассовые трубы	Для dвнутр. = 50 – 1200 мм соответственно	0.005-0.05

В общем случае коэффициент λ является функцией λ = f(R_е; ∆_экв/d) числа Рейнольдса и относительной шероховатости.

Существуют следующие зависимости для определения коэффициента трения λ:

- при ламинарном режиме

; ( ф. Ж. Пуазейля) (2.4)

- при турбулентном режиме

а) Rе<10 - гидравлически гладкие трубопроводы, λ = f(R_е);

( ф. Г. Блазиуса) (2.5)

б) 10 < Rе < 500 - коэффициент λ = f(R_е; ∆_экв/d);

(ф. А.Д. Альтшуля) (2.6)

в) Rе > 500 - гидравлически шероховатые трубопроводы, λ = f(∆_экв/d);

(ф. Б.Л. Шифринсона) (2.7)

Для трубопроводов, имеющих свободную поверхность, что соответствует безнапорному потоку, потери напора на трение определяются по формуле:

, (2.8)

где – гидравлический радиус, равный отношению площади живого сечения потока жидкости к периметру смачивания.

Для круглого трубопровода .

Обозначая , получим несколько видоизмененную формулу

, (2.9)

где С – коэффициент Шези, характеризующий шероховатость стенок трубопровода.

Решая уравнение (2.9) относительно скорости движения жидкости в безнапорном потоке и вводя обозначение i = h_тр / l (гидравлический уклон) получим

. (2.10)

Гидравлический уклон показывает потери энергии на единице длины трубопровода.

Коэффициент шероховатости определяется из формулы Маннинга

,

откуда

.