Министерство образования и науки Республики Казахстан

Карагандинский государственный технический университет

А.А. Митусов, О.С. Решетникова, Ж.Н. Нокина

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ ПО ДИСЦИПЛИНАМ

«Гидравлика», «Механика жидкостей и газов и гидропневмопривод»

Караганда 2012

Министерство образования и науки республики Казахстан

Карагандинский государственный технический университет

А.А. Митусов, О.С. Решетникова, Ж.Н. Нокина

Методические указания к выполнению лабораторных работ по дисциплинам

«Гидравлика», «Механика жидкостей и газов и гидропневмопривод»

Караганда 2012

УДК 621-82-52

Митусов А.А. Кызыров К.Б., Решетникова О.С., Нокина Ж.Н. Методические указания к лабораторным занятиям по дисциплинам «Гидравлика», «Механика жидкостей и газов и гидро-пневмопривод».- Караганда, КарГТУ, 2013 – 52 с.

Методические указания составлены в соответствии с требованиями учебного плана и программой дисциплин «Гидравлика», «Механика жидкостей и газов и гидропневмопривод» по выполнению тематики лабораторных занятий курса. Методические указания предназначены для студентов специальностей 5В071200 «Машиностроение», 5В071300 «Транспорт, транспортная техника и технологии», 5В072400 «Технологические машины и оборудование».

Утверждено Редакционно-издательским советом университета

© Карагандинский государственный технический университет

Оглавление

Лабораторная работа № 1. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ МЕСТНЫХ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ ………………..… Лабораторная работа № 2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ГИДРАВЛИЧЕСКОГО СОПРОТИВЛЕНИЯ В ТРУБЕ……………………. Лабораторная работа №3. РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИ……….. Лабораторная работа № 4. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА УРАВНЕНИЯ БЕРНУЛЛИ …………………………………………………... Лабораторная работа № 5. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА РАСХОДА РАСХОДОМЕРА ВЕНТУРИ……………………………………. Лабораторная работа № 6. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ………………………………………………….. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ…………………………….

5 15 23 30 37 43 51

Лабораторная работа № 1

Определение коэффициентов местных гидравлических сопротивлений

1 Цель работы

Закрепить экспериментом и расчетом теоретические знания по разделу «Гидравлические сопротивления»; определить опытным путем коэффициенты местных гидравлических сопротивлений.

2 Содержание работы

- изучить простейшие местные гидравлические сопротивления и обосновать наличие в них потерь энергии;

- установить взаимосвязь между потерями гидравлической энергии, коэффициентом местного сопротивления и скоростным напором;

- ознакомиться с методикой экспериментального определения коэффициентов местных сопротивлений.

3 Порядок выполнения работы

- изучить теоретический материал, представленный в методическом указании;

- ответить на контрольные вопросы;

- ознакомиться с испытательным стендом и порядком проведения лабораторной работы;

- провести эксперимент, обработать результаты исследований и представить их в виде графиков или таблиц;

- оформить и защитить отчет по лабораторной работе.

4 Оборудование для работы

Лабораторный испытательный стенд и методические указания.

5 Теоретическая часть

Местными называют потери напора или давления на изменение формы или направления потока в местах резкого изменения геометрии русла. Связано это с более быстрой, чем на прямых участках, потерей устойчивости частиц жидкости, взвихривани­ем потока и потерей энергии частиц при их столкновении между собой и со стенками русла.

В общем случае потери напора h_м или давления ∆P_м определяются по формуле Вейсбаха, где они поставлены в зависимость от скоростного напора или скоростного давления

, (1.1)

, (1.2)

где ξ - коэффициент местного сопротивления, представляющий отношение потерянного напора к скоростному напору;

v – средняя скорость движения жидкости;

 - плотность жидкости.

Величина потерь энергии определяется как разность полных напоров перед и за сопротивлением

,

а в случае равенства скоростей (v₁ = v₂)

,

где - пьезометрические напоры в сечениях перед и за сопротивлением;

- скоростные напоры в соответствующих сечениях;

₁, ₂ – коэффициенты Кориолиса, учитывающие неравномерность распределения скоростей по сечению потока.

Исследования показывают, что коэффициент местного сопротивления ξ зависит от числа Рейнольдса Re лишь при ламинарном режиме движения. B большинстве практических случаев Re>Re_кp, т.е. поток турбулентный, и влияние последних на коэффициент ξ незначительно, поэтому его значение считают зависящим только от вида и конструктивного выполнения местного сопротивления. Коэффициент ξ определяется из таблиц в зависимости от геометрического фактора. Однако, для некоторых местных сопротивлений получены и теоретические зависимости.

Простейшие местные гидравлические сопротивления можно разбить на внезапные и постепенные: 1) расширения; 2) сужения; 3) повороты русла. Более сложные сопротивления представляют собой соединения или комбинации перечисленных простейших сопротивлений.

Внезапное расширение трубопровода. При внезапном расширении поток срывается с угла и расширяется не внезапно, как трубопровод, а постепенно (рисунок 1.1), причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии в данном случае.

Потеря напора h_м определяется, согласно теореме Борда, по формуле

.

Учитывая, что S₁v₁ = S₂v₂ или , , можно записать:

, .

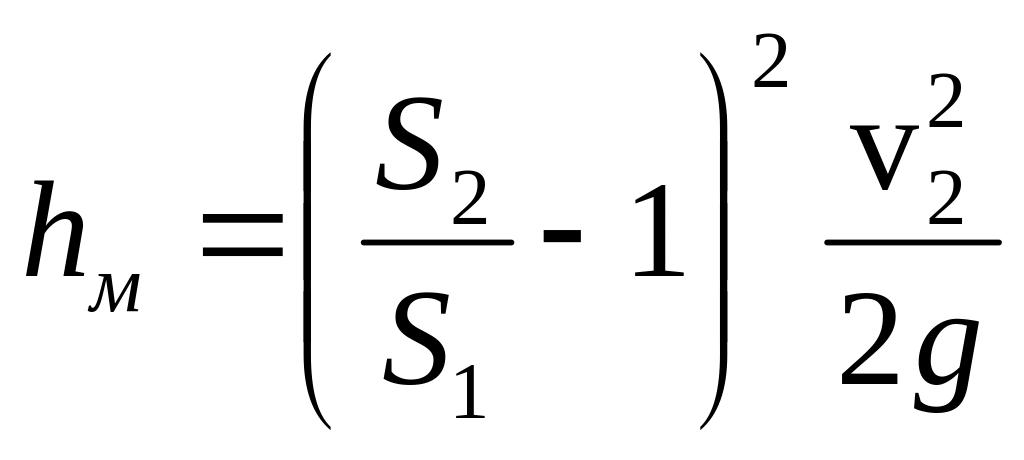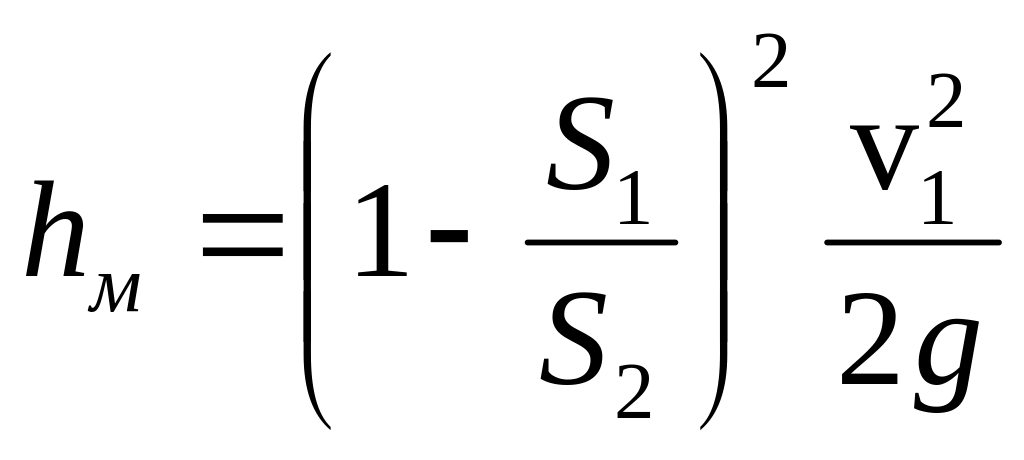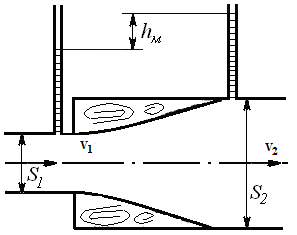
Рисунок 1.1. Схема внезапного расширения трубы

Введем обозначения:

, .

Тогда

, ,

где индексы 1 и 2 соответствуют используемой при расчете скорости v₁ и v₂.

Если диаметр трубопровода и, следовательно, скорость меняются по длине, то за расчетную скорость удобнее принимать большую из скоростей, которая соответствует меньшему диаметру трубопровода.

Внезапное сужение трубопровода. Внезапное сужение всегда вызывает меньшую потерю энергии, чем внезапное расширение при таком же соотношении площадей (рисунок 1.2). Потеря энергии обусловлена трением жидкости при входе в узкую трубу и потерями на вихреобразование. Учитывая, что потери энергии обусловлены в основном, расширением струи (увеличением струи от S_cж до S₂) коэффициент ξ определяется по формуле

.

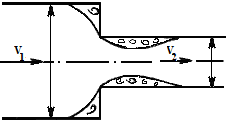
Рисунок 1.2. Схема внезапного сужения трубы

Заменяя степень сжатия струи коэффициентом сжатия

,

получим:

.

Коэффициент сжатия  можно принимать по таблице 1.1, составленной по теоретическим зависимостям Е.Н. Жуковского.

Таблица 1.1

S2­/S1	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
	0.612	0.616	0.622	0.633	0.644	0.687	0.77	0.722	0.781	1.0

Поворот трубы. Внезапный поворот трубы или колено без закругления (рисунок 1.3) вызывает значительные потери энергии, так как происходит отрыв потока и вихреобразование, причем эти потери тем больше, чем больше .

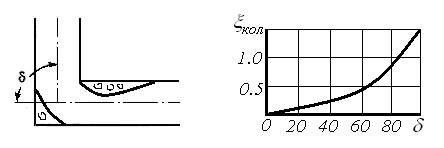
Рисунок 1.3 Рисунок 1.4

Коэффициент сопротивления колена круглого сечения _кол возрастает с увеличением очень круто (рисунок 1.4) и при достаточно 1.0.

Постепенный поворот трубы называется отводом (рисунок 1.5). Плавность поворота уменьшает интенсивность вихреобразования. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода , и при достаточно большом его значении срыв потока и связанное с ним вихреобразование устраняется полностью. Коэффициент сопротивления отвода _отв зависит от соотношения , угол , а также формы поперечного сечения трубы.

При расчете трубопровода, содержащих отводы, следует длины этих отводов включать в общую длину трубопровода, по которой подсчитывается потеря на трение, а затем к этой потере на трение необходимо добавить дополнительную потерю от кривизны, определенную коэффициентом _отв.

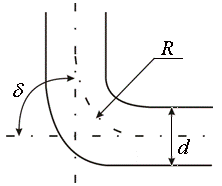
Рисунок 1.5. Плавный поворот

Постепенное расширение трубопровода (диффузор). Течение жидкости в диффузоре сопровождается уменьшением скорости и увеличением давления (рисунок 1.6).

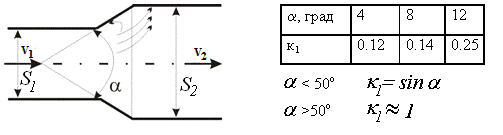
Рисунок 1.6

Движущиеся частицы преодолевают нарастающее давление за счет своей кинетической энергии, которая уменьшается вдоль диффузора, а также в направлении от оси к стенке. Слои жидкости, прилегающие к стенке, обладают столь малой кинетической энергией, что подчас они останавливаются или даже начинают двигаться обратно. Основной поток наталкивается на эти противопотоки, происходит вихреобразование и отрыв потока от стенки. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора. Кроме того, в диффузоре имеются обычные потери на трение.

Коэффициент _д диффузора определяют по формуле

,

где - коэффициент, учитывающий уменьшение потерь напора в диффузоре по сравнению с потерями напора при внезапном расширении с тем же соотношением сечений соединенных труб. Коэффициент зависит от угла конусности .

Постепенное сужение русла (конфузор). Коэффициент конфузора (рисунок 1.7) определяют в долях от потерь в напоре при внезапном сужении:

,

где - коэффициент, учитывающий уменьшение потерь напора в конфузоре по сравнению с потерями напора при внезапном сужении. Коэффициент зависит от угла сходимости .

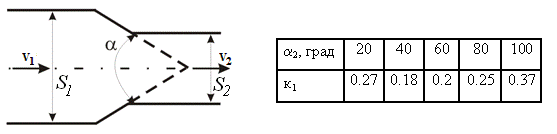
Рисунок 1.7

В общем случае рассчитанные потери на местных сопротивле­ниях суммируются (принцип наложения). Однако, для близко расположенных сопротивлений (ориентировочно l ≤ (20…50)d_э ) ξ ≠ ∑ξi. В этом случае на практике приходится определять общий коэффициент опытным путем, что и является задачей настоящей ла­бораторной работы, хотя и для достаточно простых сопротивлений. Здесь задача обратная расчетной: определить коэффициент местного сопротивления при известном, измеренном значении потерь на этом сопротивлении h_м. Формула (1.1) переписывается относительно

ξ = . (1.3)

Очевидно, опытом необходимо определить потери h_м и скорость потока v. По условию баланса полных напоров в сечениях 1 и 2 до и после сопротивления

H₁=H₂ + h_м, откуда

h_м = . (1.4)