2 Индивидуальная часть

2.1 Модели диффузии в твёрдом теле

В объеме монокристаллического твердого тела при высоких температурах возникают точечные дефекты, такие, как вакансии и межузельные атомы. В тех случаях, когда существует гра­диент концентрации собственных или примесных атомов, наличие точечных дефектов оказывает влияние на перемещение атомов, т. е. на их диффузию.

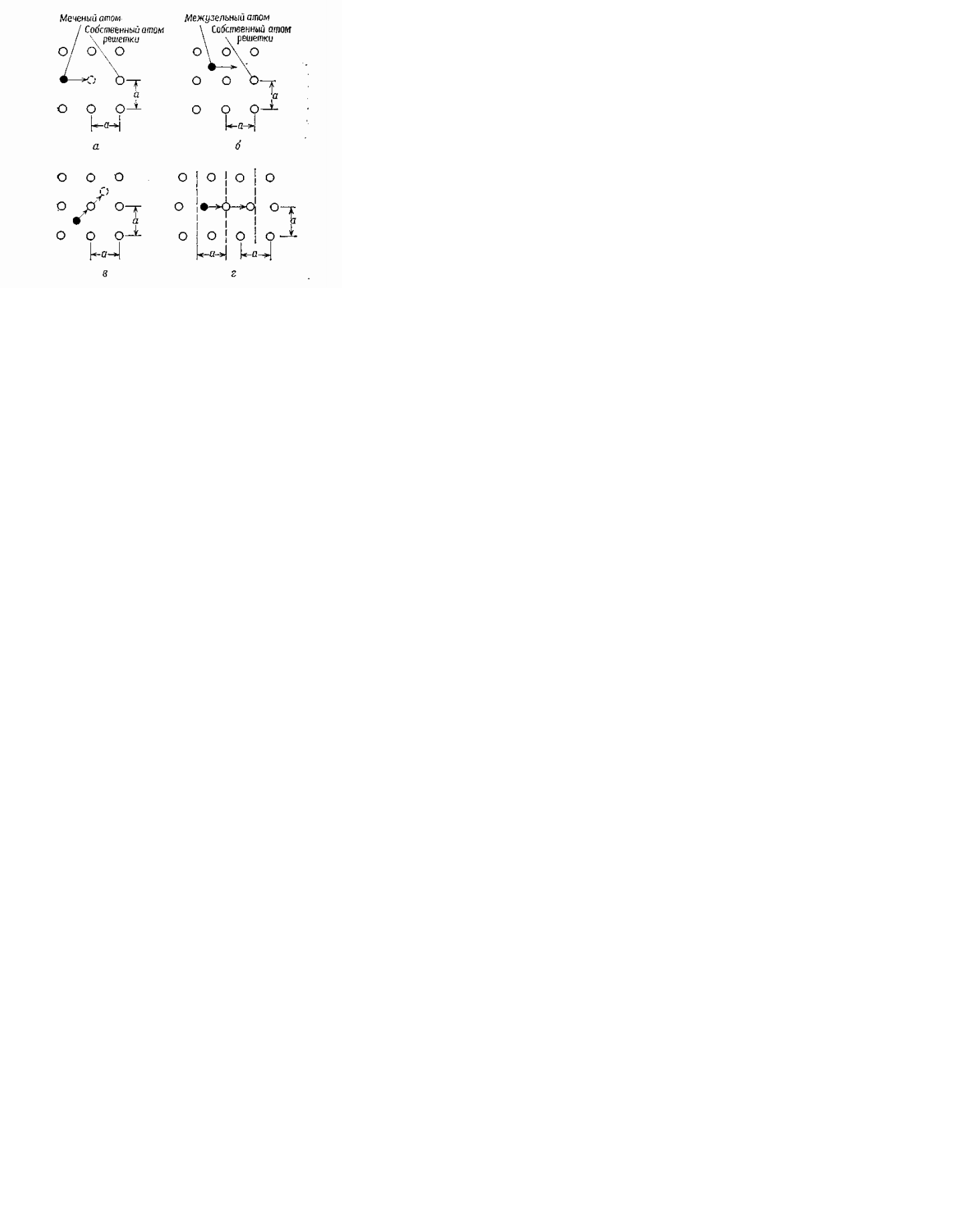
Рисунок 2.1 - Модели атомных механизмов диффузии для двумерной решетки (а — постоянная решетки) [2]. а — вакансионный механизм; 6 — межузельный механизм; в — механизм непрямого пере­мещения межузельной конфигурация (эстафетный механизм); г — краудинный механизм.

Диффузия в твердом теле мо­жет быть представлена как движение атомов диффузанта в кристаллической решетке за счет вакансий или межузельных атомов. На рисунке 2.1 с помощью упрощенной двумерной кристал­лической решетки с параметром решетки а схематически пока­заны основные атомные модели процесса диффузии [1]. Собственные атомы, занимающие при низкой температуре узлы ре­шетки, представлены светлыми кругами. Темные круги обозна­чают либо собственные, либо примесные атомы. При повышен­ной температуре атомы в узлах решетки колеблются вблизи равновесного положения. Время от времени они приобретают достаточную энергию для того, чтобы удалиться от указанного положения в узле решетки, и становятся межузельными ато­мами оставляя в решетке вакансию. Такой механизм диффузии, когда соседний атом, будь то атом примеси или собственный атом кристалла, мигрирует на место вакансии, называется вакансионным (рисунок 2.1,а). Если мигрирующий атом является соб­ственным атомом, то процесс диффузии называют самодиффу­зией, а если примесным, — примесной диффузией. Эксперимен­ты по самодиффузии обычно проводят путем введения радиоак­тивных изотопов собственных атомов в кристалл (рисунок 2.1, а).

Механизм диффузии, при котором атом переходит из одного положения в другое, не попадая при этом в узлы кристалличе­ской решетки, называется механизмом прямого перемещения атомов по междоузлиям (рисунок 2.1, б). Реализация этого механиз­ма наиболее вероятна в случае диффузии атомов малых разме­ров. Энергия активации, необходимая для диффузии межузельных атомов, ниже энергии активации для диффузии атомов ре­шетки по вакансионному механизму.

На рисунке 2.1,в показано движение межузельных атомов, ког­да в процессе перемещения они вытесняют атом решетки и за­мещают его, вытесненный атом в свою очередь становится межузельным. Такое перемещение собственных или примесных ато­мов называют механизмом непрямого перемещения атомов по междоузлиям или эстафетным механизмом. С указанным меха­низмом непосредственно связан и краудионный механизм, при котором межузельный атом, расположенный посередине между двумя узлами решетки, перемещается к одному из них, смещая при этом атом, расположенный в узле. Вытесненный атом ста­новится межузельным и занимает промежуточное положение в решетке (рисунок 2.1,г).

С помощью методов статистической термодинамики можно оценить необходимую энергию активации для образования то­чечных дефектов в каждом кристалле и определить их концент­рацию что может дать возможность разработать модель диффу­зии в этом кристалле [21]. Затем полученные теоретические ре­зультаты можно сравнить с экспериментальными данными. Установлено, например, что в кремнии диффузия примесей эле­ментов III и V групп периодической системы происходит в ос­новном по вакансионному механизму. Элементы I и VIII групп, имеющие малый ионный радиус, относятся к быстродиффундирующнм примесям в кремнии. Предполагается, что их диффузия происходит по механизму прямого перемещения атомов по меж­доузлиям, Однако эти простые атомные механизмы не являются адекватными для описания процессов диффузии в тех случаях, когда концентрация примеси достаточно высока, кристалл со­держит дислокации или в решетке присутствуют другие приме­си с высокой концентрацией. При низкой концентрации приме­си и низкой плотности дислокаций процесс диффузии может быть описан феноменологической теорией диффузии с исполь­зованием закона диффузии Фика с постоянным значением ко­эффициента диффузии. Математические выражения, отражаю­щие процесс диффузии, получают путем решения уравнения диффузии Фика. При этом коэффициенты диффузии различных элементов определяют для разных температур. В случае высо­кой концентрации примеси концентрационная зависимость ко­эффициентов диффузии связана с предполагаемым механизмом или механизмами диффузионных процессов на атомном уровне.

2.2 Одномерное уравнение диффузии Фика

В 1855 г. Фик предложил теорию диффузии. В основу этой теории положена аналогия между процессами переноса в жид­ких растворах и тепла за счет теплопроводности [2]. Фик пред­положил, что в разбавленных жидких или газообразных раство­рах в отсутствие конвекции перенос атомов через площадку единичной площади при одномерном направлении потока может быть описан следующим уравнением:

(2.1)

где J — скорость переноса растворенного вещества через сече­ние единичной площади, или диффузионный поток; С — концент­рация растворенного вещества, которая, как предполагается, за­висит только от x и t; х — ось координат, совпадающая с направлением потока вещества; t и D — соответственно время и коэффициент диффузии.

Уравнение (2.1) показывает, что локальная скорость пере­носа растворенного вещества (локальная скорость диффузии) через сечение единичной площади за единицу времени пропор­циональна градиенту концентрации растворенного вещества, а в качестве коэффициента пропорциональности выступает коэф­фициент диффузии растворенного вещества. Знак минус в пра­вой части уравнения (2.1) означает, что процесс переноса ве­щества происходит в направлении уменьшения концентрации растворенного вещества (т. е. градиент отрицательный). Урав­нение (2.1) называют первым законом Фика.

Из закона сохранения вещества следует, что изменение кон­центрации растворенного вещества со временем должно быть равно уменьшению диффузионного потока в том же объеме, где произошло изменение концентрации, т. е.

(2.2)

Подстановка уравнения (5,1) в уравнение (5.2) приводит ко второму закону Фика для одномерного случая:

(2.3)

При низких концентрациях растворенного вещества коэффи­циент диффузии можно считать постоянным и уравнение (5.3) можно записать в виде

(2.4)

Уравнение (2.4) часто называют простым диффузионным уравнением Фика. В этом уравнении D имеет размерность см²/с или мкм²/ч, а С — см^-3. Получены решения уравнения (2.4) для различных простых начальных и граничных условий.

2.3.1. Постоянные коэффициенты диффузии

Диффузию примеси для формирования р-n переходов мож­но легко получить при двух условиях: постоянной поверхностной концентрации (диффузии из бесконечного источника) и посто­янном числе легирующих атомов (диффузия из ограниченного источника). В первом случае примесные атомы диффунди­руют из источника, нанесенного на поверхность кремниевой под­ложки. Такой источник поддерживает постоянную поверхност­ную концентрацию в течение всего процесса диффузии. Во вто­ром случае небольшое количество легирующего вещества осаж­дается на поверхность кремния. Математически такое мгновен­ное осаждение легирующего вещества соответствует дельтафункции. Это условие может быть достигнуто за счет диффузии при низкой температуре в качестве первой стадии диффузион­ного процесса. Диффузия из ионно-имплантированных слоев мо­жет служить примером второго случая. В данном разделе при­ведены решения диффузионного уравнения Фика для обоих слу­чаев.

Диффузия из бесконечного источника. Начальные условия при ( t = 0 формулируются как

С (х,0) = 0 (2.5)

Граничные условия можно представить в виде

С(0,t)= (2.6)

и

С(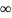 >t) = 0 (2.7)

Тогда решение уравнения (2.4), которое удовлетворяет на­чальным и граничным условиям, можно записать как

(2.8)

где C_s (см^-3) — постоянная поверхностная концентрация, D (см²/с) — постоянный коэффициент диффузии, х (см) — рас­стояние по оси координат с учетом, что х = 0 находится на по­верхности кремния, t (с)—время диффузии и erfc — дополни­тельная функция ошибок.

Рисунок 2.2 - Нормированное распределение по дополнительной функции ошибок.

На рисунке2.2 приведен нормированный профиль концентрации для распределения примеси согласно дополнительной функции ошибок [уравнение (2.8)]. Глубина, на которой концентрация диффундирующей примеси равняется концентрации исходной примеси в подложке, называется металлургическим перехо­дом . Для можно записать C( )=C_п, где C_п — концентра­ция исходной примеси в подложке. Предполагая, что подложка легирована примесью противоположного диффузанту типа проводимости и используя для отображения концентрации лога­рифмическую шкалу, можно определить результирующую кон­центрацию легирующих элементов │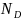 — │ вблизи р—n перехода.

Диффузия из ограниченного источника. Предположим, что на поверхности кремниевой подложки осажден тонкий слой ле­гирующего вещества с фиксированным или постоянным общим числом атомов S на единицу площади. Кремниевая подложка, в которую проводится диффузия, легирована примесью противо­положного типа проводимости с концентрацией С (см^-3). На­чальные и граничные условия для решения диффузионного урав­нения (2.4) выглядят следующим образом:

начальные условия:

С(х,0) = 0 (2.9)

граничные условия:

(2.10)

(2.11)

Решение диффузионного уравнения (24), которое удовлетво­ряет условиям, записанным в уравнениях (2.9) — (2.11), имеет следующий вид:

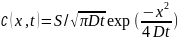(2.12)

Полагая х = 0, получим величину поверхностной концентра­ции

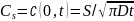(2.13)

Уравнение (2.12) называют гауссовым распределением, а условие, при котором происходит диффузия, относят к диффу­зии с предварительным осаждением.

Перераспределение в диффузионных слоях. В технологии формирования биполярных линейных ИС важным этапом явля­ется диффузионное перераспределение примеси из сильнолеги­рованных диффузионных слоев, полученных на предшествую­щем этапе. Диффузионное перераспределение в неокисляющей среде изучено достаточно широко. В технологии формирования СБИС с целью сохранения мелкой глубины диффузионных слоев процессы перераспределения интенсивно не используются. Од­нако некоторое диффузионное перераспределение может проис­ходить во время отжига ионно-имплантированных слоев для электрической активации внедренной примеси при температуре выше 1000 °С. Было получено решение уравнения Фика (2.4) для процесса диффузионного перераспределения с начальным гауссовым распределением ионно-имплантированной примеси [3]

Решение уравнения процесса диффузионного перераспреде­ления примеси в окислительной атмосфере осложняется необ­ходимостью учета движущейся границы. Для этого случая не было обнаружено решения в аналитическом виде. Математиче­ская формулировка диффузии в окислительной атмосфере полу­чена из конкретных первоначальных профилей распределения [3], однако такое решение содержит выражения, которые требу­ют проведения численного интегрирования.