1.2. Элементы кристаллографии
1.2.1. Кристаллическая решетка
В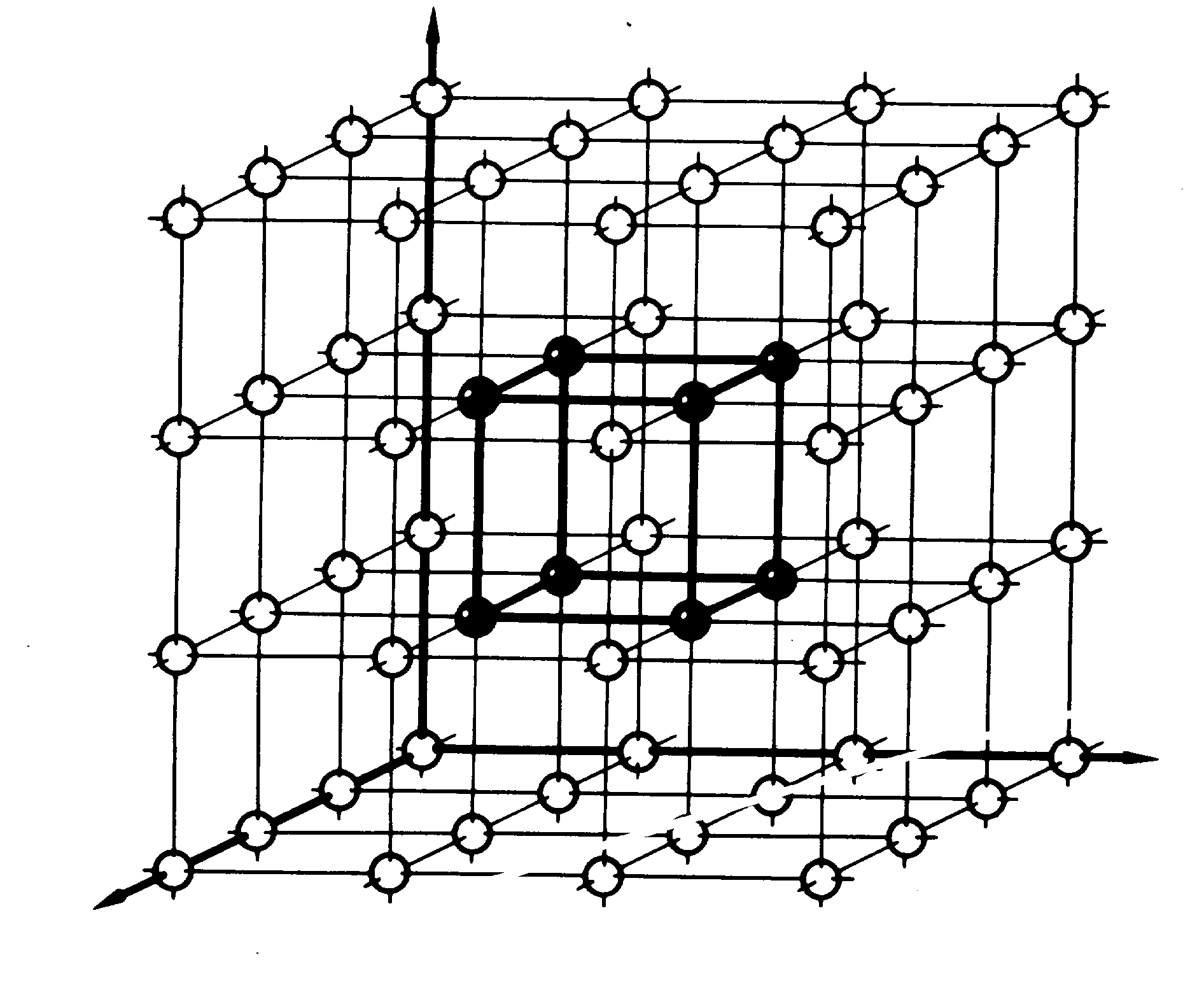
кристалле частицы (ионы, атомы, молекулы),
из которых построен кристалл, сближены
до соприкосновения и располагаются
закономерно по разным направлениям
(рис 1.1).
Рис. 1.1. Схематическое изображение простейшей кубической пространственной
решетки металла и его элементарной ячейки (выделена более толстой линией).
Атомы расположены равномерно во всех трех направлениях.
Если в кристалле провести три ортогональных направления x, y, z, то расстояния между частицами, расположенным по этим направлениям в общем случае неодинаковы и равны а, в и с соответственно.
Плоскости, параллельные координатным плоскостям, находящиеся на расстоянии а, в, с, разбивают кристалл на множество параллелепипедов, равных и параллельно ориентированных. Наименьший параллелепипед называют элементарной ячейкой. Последовательное перемещение его образуют кристаллическую решетку. Вершины параллелепипеда называют узлами пространственной решетки. С этими узлами совпадают центры тяжести частиц, из которых построен кристалл.
Для описания элементарной ячейки кристалла решетки используют 6 величин: 3 отрезка, равные расстояниям а, в, с до ближайших частиц по осям координат, и 3 угла α, β, γ между этими отрезками.
Соотношения между этими величинами определяются симметрией, согласно которой все кристаллы подразделяются на семь систем (табл. 1.1).
Табл. 1.1
Кристаллические системы элементов
Система |
Ребра |
Углы |
Триклинная Моноклинная Ромбическая Ромбоэдрическая Гексагональная Тетрагональная Кубическая |
а ≠ в ≠ с а ≠ в ≠ с а ≠ в ≠ с а = в =с а = в ≠ с а = в ≠ с а = в = с |
α ≠ β ≠ γ α = β = 90º γ ≠ 90º α = β = γ = 90º α = β = γ ≠ 90º α = β = 90º γ = 120º α = β = γ = 90º α = β = γ = 90º |
Размер элементарной ячейки кристаллической решетки оценивают отрезки а, в, с. Их называют периодами решетки.
В большинстве случаев решетки имеют сложное строение, т.к. частицы находятся не только в узлах, но и на гранях или в центре решетки (рис. 1.2). О степени сложности судят по числу частиц, приходящихся на одну элементарную ячейку. В простой пространственной решетке всегда на одну ячейку приходится одна частица. В каждой ячейке имеется восемь вершин, но каждая частица в вершине относится, в свою очередь, к восьми ячейкам. Таким образом, от узла на долю каждой ячейки приходится 1/8 объема, а всего узлов в ячейке – 8, следовательно, на ячейку приходится одна частица.
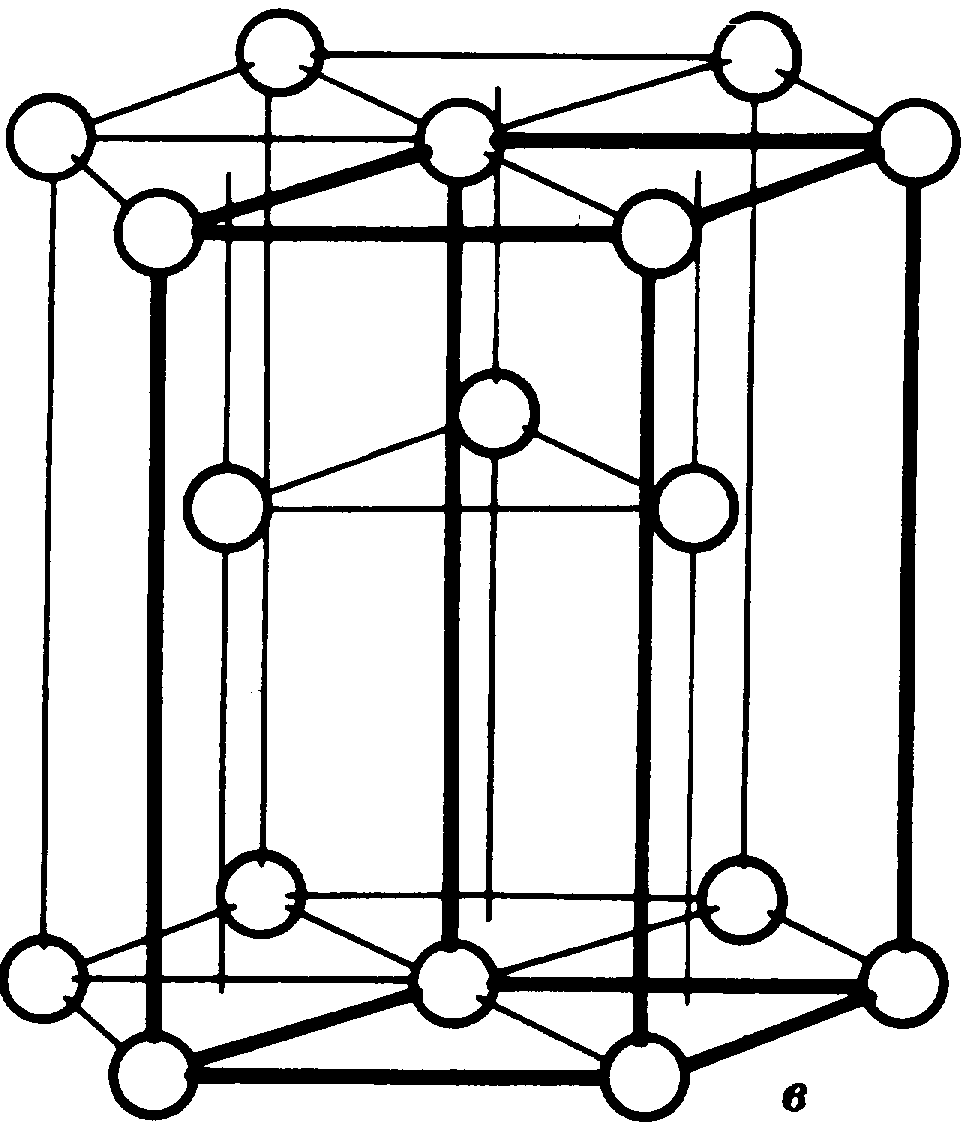
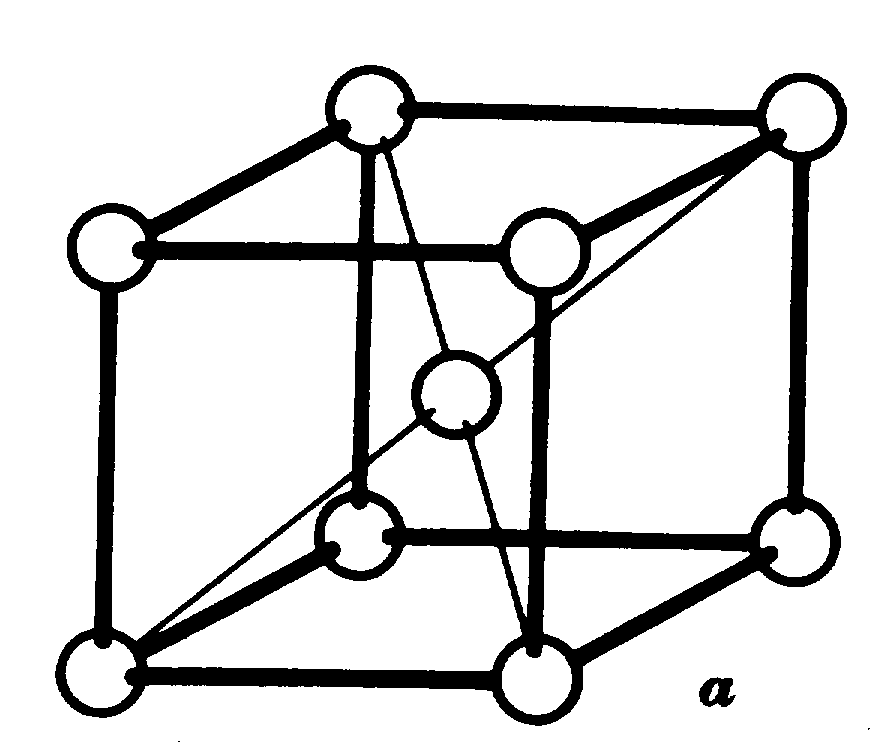
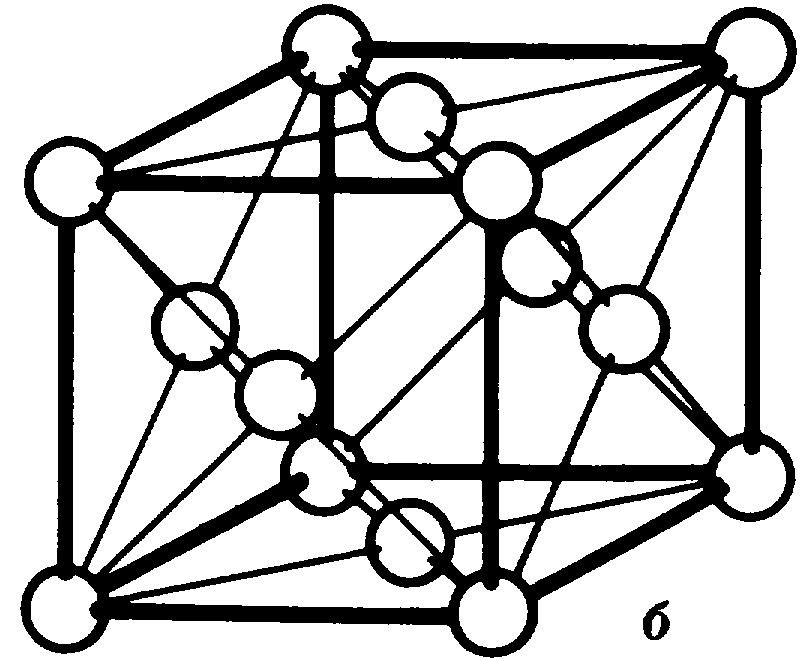
Рис.1.2. Элементарные ячейки трех наиболее типичных для металлов
кристаллических решеток: а - объемноцентрическая кубическая (ОЦК) – α-железо;
б- гранецентрическая кубическая (ГЦК) – γ-железо, медь, никель;
в – гексагональная плотноупакованная (ГП) – цинк.
В сложной пространственной решетке на одну ячейку приходится больше одной частицы. На объемно-центрированную ячейку приходятся две частицы: одна - от вершины и другая - центрирующая, которая относится только к данной ячейке. В гранецентрированной ячейке имеются четыре частицы: одна - от вершины и три - от шести центрированных плоскостей, так как частица, находящаяся в центре плоскости, относится одновременно к двум ячейкам.
Система, период и число частиц, приходящихся на элементарную ячейку, полностью определяют расположение частиц в кристалле. Дополнительными характеристиками кристаллической решетки являются координационное число и коэффициент компактности.
Ч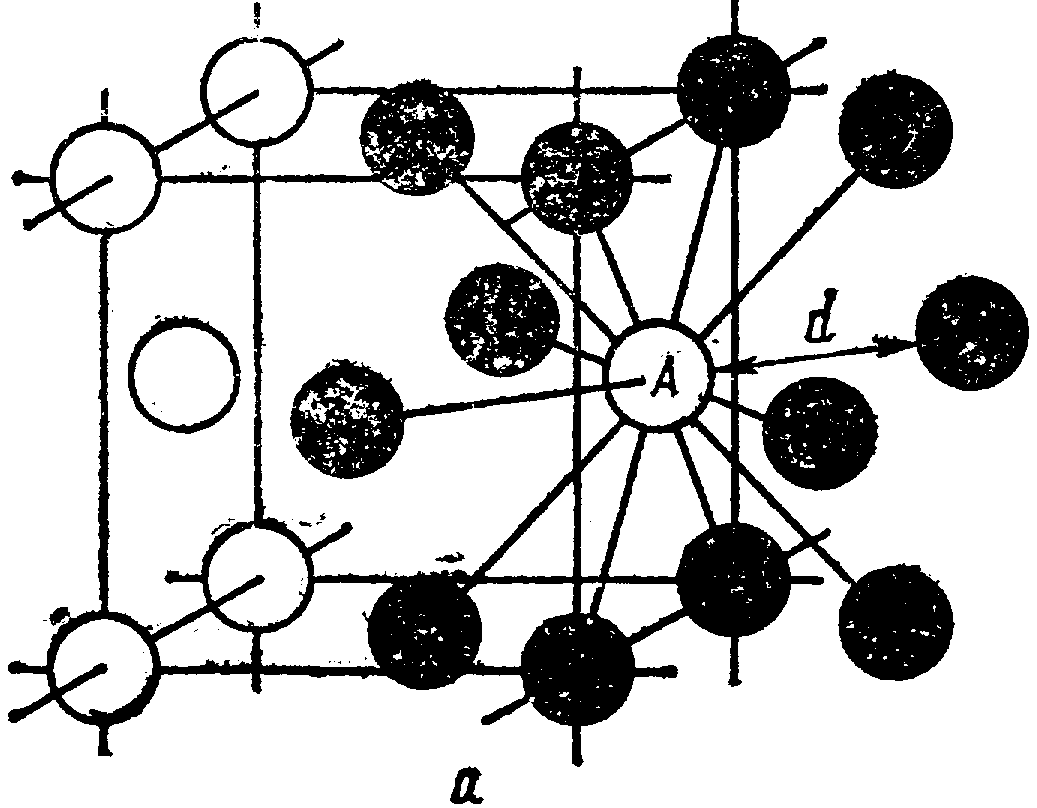
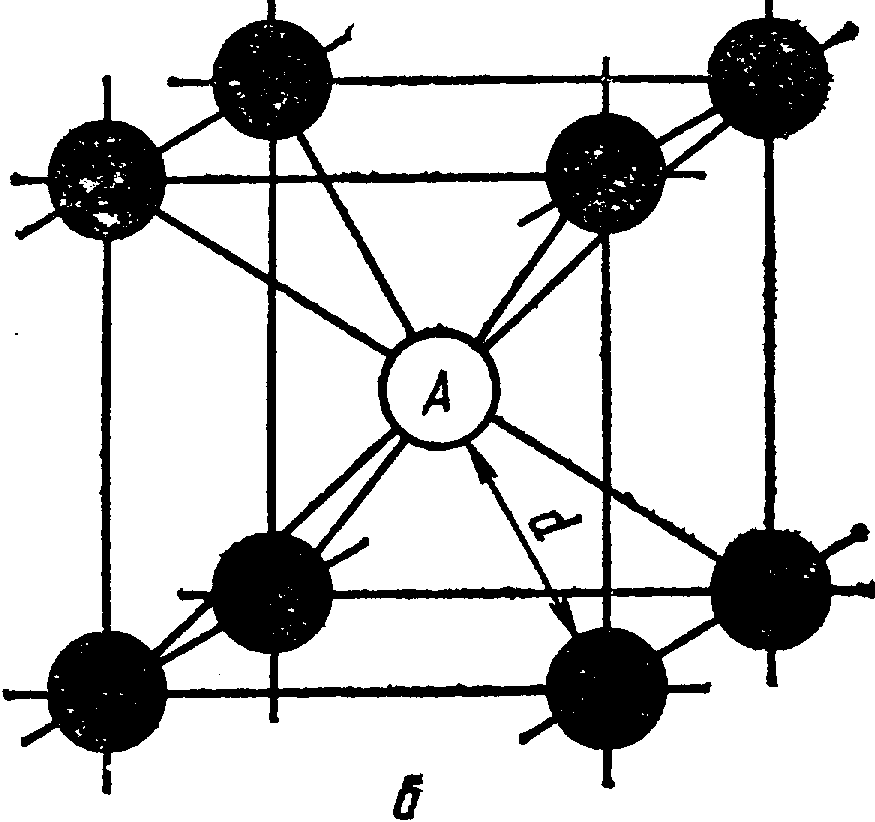исло
ближайших равноудаленных частиц
определяет координационное число К
(рис. 1.3). Например, в решетке объемно
– центрированного куба (ОЦК) для
каждого атома число таких соседей будет
равно 8 (К8). Для простой кубической
решетки координационное число будет 6
(К6), для гранецентрированной кубической
решетки (ГЦК) – 12 (К12).
Рис. 1.3. Определение координационного числа в кристаллической решетке
а – ГЦК , б - ОЦК
Отношение объема всех частиц, приходящихся на одну элементарную ячейку, ко всему объему элементарной ячейки определяет коэффициент компактности. Для простой кубической решетки его значение равно 0.52, для ОЦК – 0.68 и для ГЦК – 0.47.
Оставшееся пространство образуют поры, которые подразделяют на октаэдрические и тетраэдрические. На рис.1.4. центры этих пор показаны маленькими точками на ГЦК решетке. Радиус октаэдрической поры составляет 0.41, а тетраэдрической поры – лишь 0.22 радиуса частицы.
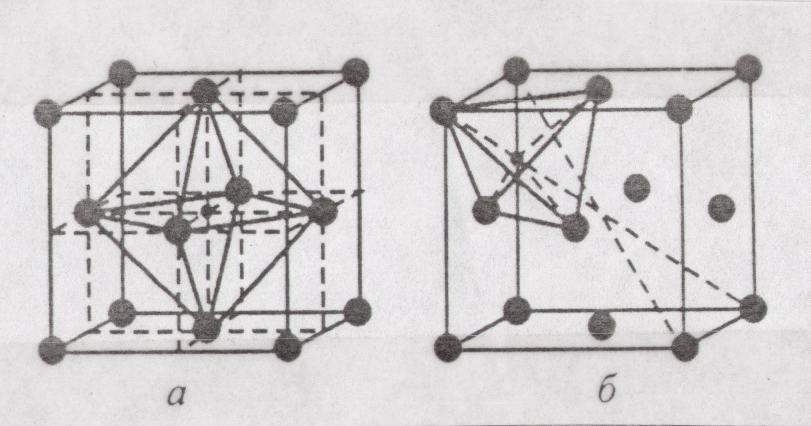
Рис. 1.4. Поры в кристаллической решетке: а – тетраэдрическая, б - октаэдрическая
Для многих металлов характерна плотная упаковка частиц. Если частицы изобразить в виде шаров, то получатся структуры, показанные на рис. 1.5.
Шестигранная призма на рис. 1.5а изображает гексагональную плотноупакованную решетку (ГП) – на первый слой шаров (А) в лунки накладывают второй слой (В). Если третий слой шаров укладывается над первым слоем – получается ГП-решетка. Если третий слой не укладывается над первым, а только четвертый повторяет первый слой шаров, то получается гранецентрическая кубическая решетка (ГЦК) (рис 1.5в).
Если частицы обладают сферической симметрией, то отношение периодов с/а = 1,633 (как в ГП кристаллической решетке, где а=в≠с, α=β=90о , γ=120о)
При отклонении частиц от сферической симметрии возможно образование гексагональных структур с соотношением периодов, отличающихся от 1.633, а также ОЦК – структур (рис.1.5.б).
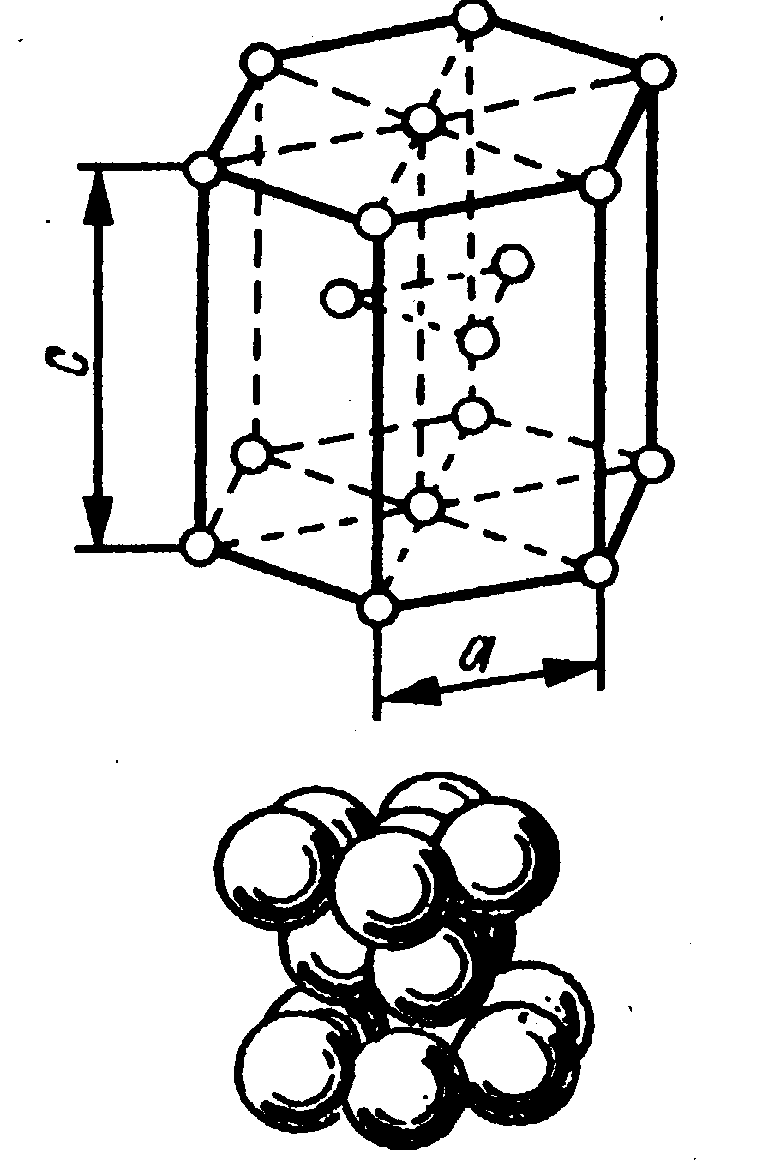
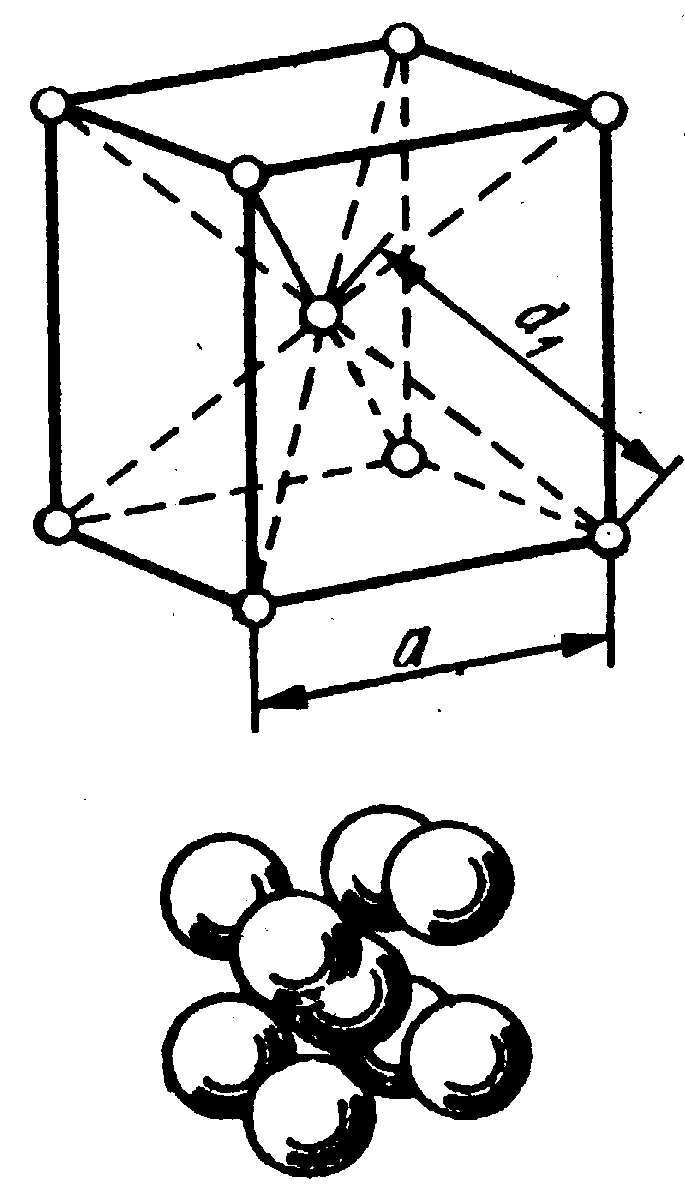
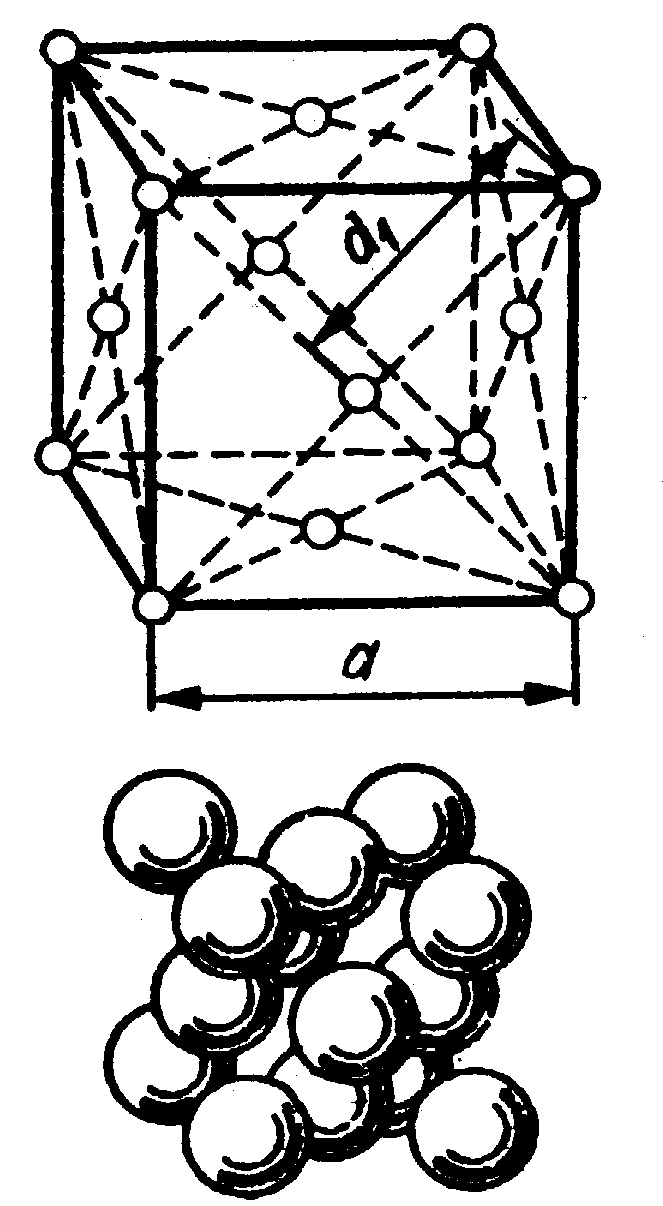
а б в
Рис.1.5. Упаковка частиц в кристалле: а – ГП, б – ОЦК, в – ГЦК