5. Задача про мінімальне з'єднання

Теорема Келі становить інтерес у зв'язку з наступною практичною задачею.

Нехай для деякої множини міст відома вартість будівлі дороги між будь-якими двома містами . Яка повинна бути мережа доріг між містами, що входять в , щоб по ній можна було проїхати з будь-якого міста в будь-яке місто й щоб вартість цієї мережі було мінімальною?

Аналогічні задачі виникають при проектуванні мереж зв'язку, електричних і трубопровідних мереж і т.п. задачі цього роду називають задачами про мінімальне з'єднання.

Мовою теорії графів задача про мінімальне з'єднання формулюється в такий спосіб. Нехай – зв'язний граф, кожному ребру якого приписується деяка міра (довжина, вага, вартість і т.п.), потрібно знайти зв'язний остовний підграф графа з мінімальною мірою . Очевидно, що повинен бути деревом: якби містив цикл, то можна було б зменшити , видаливши одне з його ребер.

Як показує теорема Келі, рішення цієї задачі простим перебором вимагає надзвичайно більших обчислень навіть при невеликому числі вершин (при , існує дерев). Однак для її рішення є наступний ефективний алгоритм, запропонований чеським математиком Борувкой.

Крок 1. Вибирається ребро з найменшою мірою. Позначимо через остовний підграф .

Крок -й, . Нехай на -м кроці побудований остовний підграф ,який не містить циклів й містить компонент зв’язності. Тоді , . Якщо , то ; по теоремі 4 до графа можна приєднати ребро так, щоб отриманий граф не містив циклів (тому що цикломатичне число при цьому не збільшується).

На кроці ми будуємо граф , вибираючи так, щоб міра була мінімальною. Якщо таких ребер декілька, то вибираємо в якості будь-яке з них. Якщо ж , те , і граф є деревом. Це дерево називають звичайно економічним.

Твердження. Міра економічного дерева мінімальна.

Доказ. Допустимо, що наше припущення невірно. Нехай , відмінне від дерево мінімальної міри , що є кістяком графа ; – ребро з найменшим номером з , що не втримується в. Серед таких дерев виберемо те, у якому число максимально.

У дереві найдеться ланцюг , що з'єднує й (див. мал. 4.30);

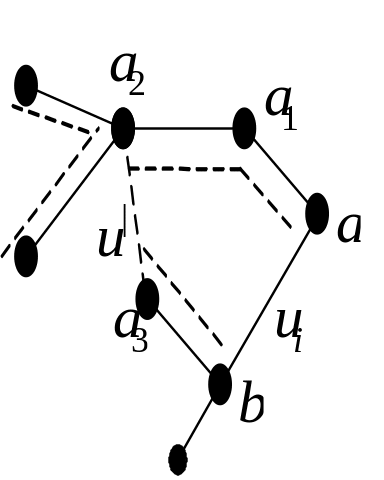
Рис. 4.30

у ньому ребра графа намальовані суцільними лініями, ребра – пунктирними. Разом з вона утворить цикл, що містить хоча б одне ребро , що не належить (дерево не містить циклів). Приєднавши до ребро й видаливши , одержимо нове дерево , що також містить всі вершини графа .

За умовою, і, отже, . З іншого боку, ребро не утворить із ребрами циклу, тому що всі вони входять у дерево . Якби , то при побудові дерева треба було б використати ребро , а не . Отже, . Отже, дерево має мінімальну міру й містить ребра . Це суперечить вибору дерева . Таким чином, економічне дерево має мінімальну міру.

Контрольні питання

1. Наведіть ряд ознак, що дозволяють розпізнати в даному графі дерево.

2. Який граф називається позначеним? Які позначені графи вважаються однаковими?

3. Сформулюйте теорему Келі.

4. Дайте визначення остовного підграфа.

5. Яка необхідна та достатня умова того, щоб граф мав більше одного остову?

6. Чому дорівнює число остовних дерев у простому зв’язному графі?

7. Сформулюйте задачу про мінімальні з’єднання мовою теорії графів.

8. Яке дерево називають економічним?