12

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ РАДІОЕЛЕКТРОНІКИ

Лекція 4 Тема: "Характеристика дерев. Остови графу. Задача про мінімальне з’єднання." Дисципліна : "Дискретна математика"

Викладач: Гусарова І. Г.

Харків,2014

Мета лекції: розглянути означення, характеристики, властивості дерев та остовів графа; також розглянути задачу про мінімальне з’єднання.

Зміст:

1. Характеристика дерев.

2. Позначені дерева.

3. Остови графа.

4. Алгоритм пошуку у глибину.

5. Задача про мінімальне з’єднання.

Базові Поняття та Ключові Слова :

1. Дерево.

2. Позначене дерево.

3. Остовний підграф.

4. Матриця Кірхгофа.

5. Економічне дерево.

1. Характеристика дерев

Приведемо ряд ознак, що дозволяють розпізнати в даному графі дерево.

Теорема 1. Нехай граф з вершинами, де ; наступні його властивості еквівалентні й визначають як дерево:

1) – зв'язний і не містить циклів;

2) – зв'язний і його цикломатичне число ;

3) – не містить циклів і має ребро;

4) – зв'язний і має ребро;

5) не містить циклів, але додавання ребра між двома будь-якими вершинами приводить до появи одного (і тільки одного) циклу;

6) зв'язний, але втрачає цю властивість після видалення будь-якого ребра;

7) усяка пара вершин з'єднана ланцюгом, і тільки однієї.

Доведення. Покажемо, що кожна наступна властивість випливає з попереднього, а властивість 1 випливає із властивості 7. Нехай – кількість ребер, – число компонентів зв’язності.

1) 2) у силу наслідку 1.

2) 3): якщо , то .

3) 4): якщо й , то .

4) 5): якщо й , то , тобто не містить циклів. Якщо ж додати ребро, то одержимо , і з'являється один і тільки один цикл.

5) 6): якби не був зв'язний, то в ньому були б дві вершини й , не з'єднані ніяким ланцюгом. У такому випадку приєднання ребра не приводить до появи циклу, що суперечить 5). Виходить, зв'язний, . Крім того , отже, , тобто . Якщо ж видалити будь-яке ребро, то й залишається ; тому , звідки й стає незв'язним.

6) 7): тому що зв'язно, то будь-які дві вершини з'єднані ланцюгом. Такий ланцюг може бути тільки одна, інакше видалення ребра, що належить другого ланцюга й не приналежного першої, не порушило б зв’язності.

7) 1): якщо граф має цикл, то в ньому існує хоча б одна пара вершин, з'єднаних двома ланцюгами.

2. Позначені дерева. Кількість позначених дерев

У зв'язку з теоремою 3 виникає питання про число різних дерев, які можна одержати з даного зв'язного позначеного графа.

Визначення. Граф називається позначеним, якщо його вершини відрізняються одна від іншої якими-небудь позначками. Наприклад, номерами. На мал. 4.8 граф позначений, на мал. 4.9 – ні.

Визначення. Два позначених графи вважаються однаковими (не різними), якщо між ними існує ізоморфізм, що зберігає позначки їхніх вершин. Всі позначені дерева на мал. 4.25 різні, хоча дерева з номерами (1) – (12) ізоморфні між собою, і дерева (13) – (16) ізоморфні між собою.

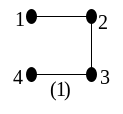
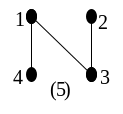
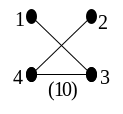
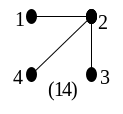
Рис. 4.25

Позначені графи на мал. 4.7 і мал. 4.8 однакові. Одна з перших постановок цього питання пов'язана з дослідженням хімічних структурних формул. Тут наведений один результат, що ставиться до цієї області.

Теорема 2. (Келі) Існує точно різних позначених дерев з позначених вершин (інакше: повний позначений граф має точно різних кістяків).

На мал. 4.25 показані 16 різних позначених дерев, що виходять при .

Доведення. Висновок з теореми Кірхгофа.