2. Оценка дебита для элемента пятиточечной системы разработки

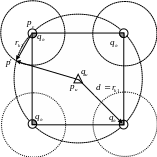
Рис.2. Схематизация фильтрационных потоков в пятиточечной системе

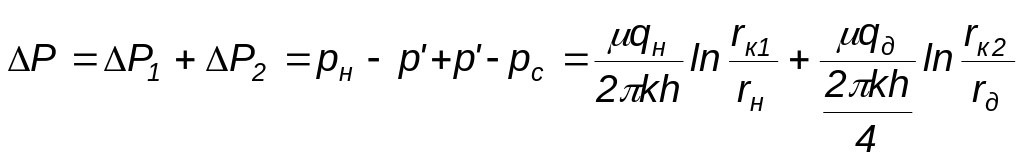
если принять , и

3. Оценка дебита для элемента семиточечной системы разработки

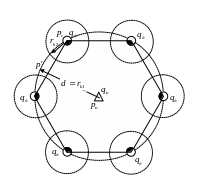
Рис.3. Схематизация фильтрационных потоков в семиточечной системе

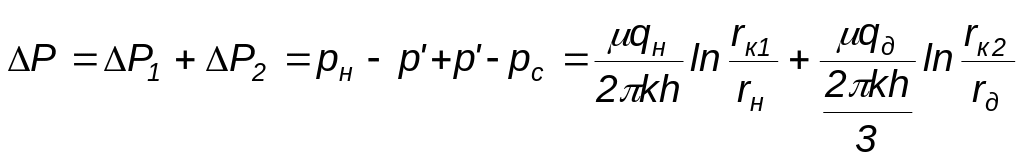
если принять , , также можно получить формулу для обоснования дебита исходя из условия

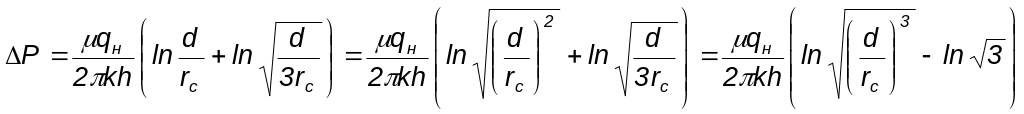
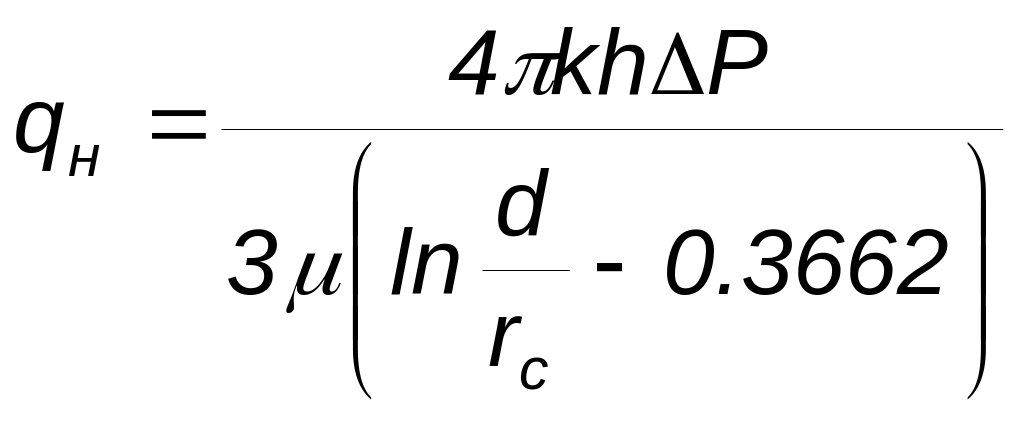
4. Оценка дебитов при трехрядной системе размещения скважин

Рис.4. Схематизация фильтрационных потоков в трехрядной системе

Приводимые далее выражения справедливы при условии, что .

Внутренние сопротивления при течении жидкости вблизи нагнетательной скважины рассчитываются при условии, что плоско-радиальный поток сменяется плоско-параллельным на удалении от скважины . Это получается из предположения, что полупериметр окружности обращенной вовнутрь элемента равен расстоянию между скважинами в ряду, то если формирующемуся прямолинейно-параллельному фронту вытеснения

Внешние фильтрационные сопротивления между рядом нагнетательных скважин и первым рядом добывающих скважин будут равны

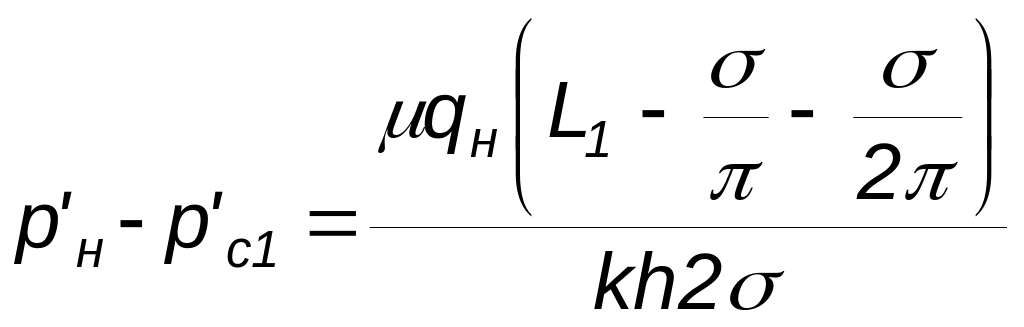
Внутренние сопротивления вблизи добывающих скважин первого ряда при изменении типа течения жидкости равны:

при условии, что или

Внешние сопротивления при течении жидкости между первым и вторым (стягивающим) рядами

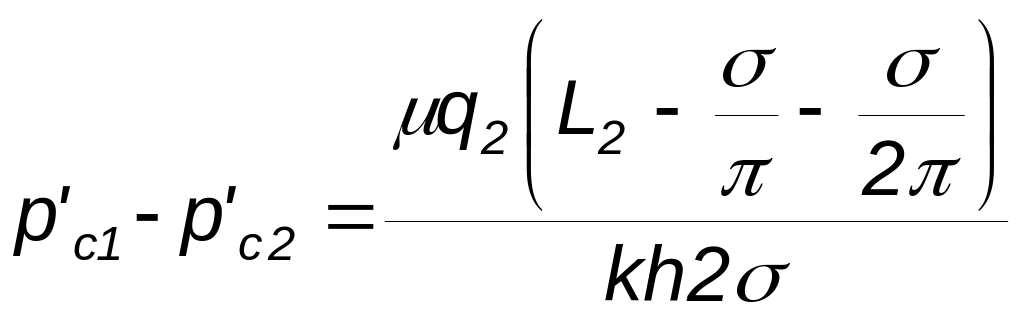
Внутренние сопротивления вблизи добывающих скважин второго ряда при изменении типа течения жидкости

Перепишем выражения для потерь давления

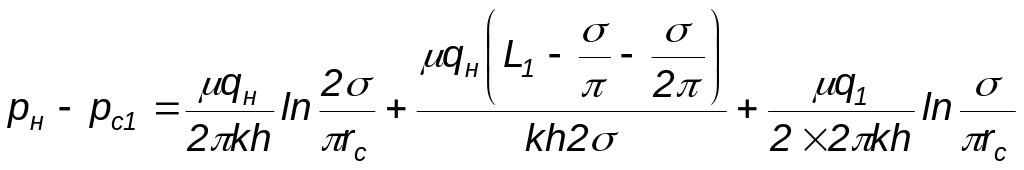
Для определения дебита скважин каждого ряда необходимо решить систему уравнений:

(1)

(2)

(3)

где ;

;

.

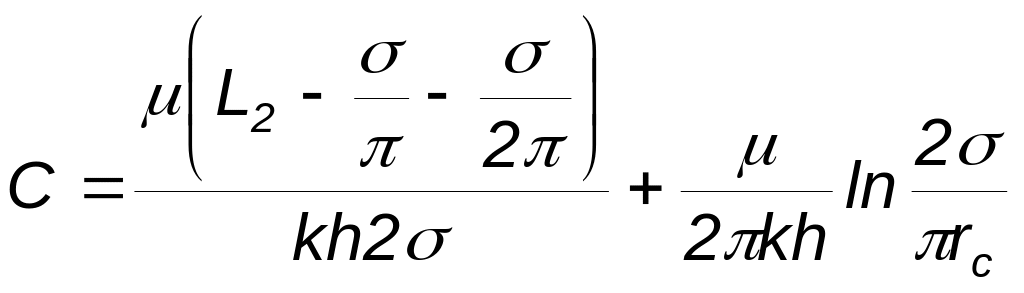Выразим из первого уравнения подставляя вместо выражение (3):

таким образом, равен:

(4)

Выразим из второго равенства

(5)

приравняем выражения (4) и (5)

и выразим

зная используя выражение (4) определим

3.О зависимости дебита скважин от времени

Промышленная добыча нефти началась задолго до того, как было установлено, что фильтрация нефти в пласте подчиняется законам подземной гидравлики. Тем не менее, необходимо было с открытием каждого месторождения решать важные задачи, такие как: следует ли на данном месторождении бурить следующую скважину, вкладывать деньги в обустройство месторождения и строительство нефтепровода. Эти и многие другие вопросы упирались в прогнозирование добычи нефти со скважины или их группы. При отсутствии теории прогноз проводился на основании обобщения опыта работы ранее пробуренных скважин. При большом их числе и длительном сроке работы необходимо было пользоваться методами статистики. Так, было установлено, что по большинству скважин, режим работы которых не нарушается частыми ремонтами, логарифм дебита нефти изменяется по отношению к первоначальному пропорционально времени, то есть:

.

Отсюда потенцированием получаем:

.

Такой вывод был сделан в работах американских инженеров С. Била и Х. Льюиса, а также бакинца С.И.Чарноцкого.

Аналогичная формула закона падения дебита во времени для скважины, эксплуатирующей залежь в режиме растворенного газа, получена теоретически С.Л.Лейбензоном в 1923 году в период его работы в Баку. В то время разработка всех месторождений велась на истощение, для добычи нефти из скважин применяли компрессорный газлифт. В последующем при разработке месторождений с закачкой воды было установлено, что падение дебита нефти по экспоненциальному закону характерно и в условиях прогрессирующего обводнения скважин. Такое положение было обосновано в работах Э.Б. Мухарского, В.Д. Лысенко и И.Г.Пермякова, сделавших свои выводы на основе многочисленных данных по разработке нефтяных месторождений Урало-Поволжья (Башкортостан, Татарстан, Самарская и Саратовская области). Особенно много для популяризации экспоненциального закона сделали В.Д. Лысенко и Э.Б.Мухарский, которые связали декремент (быстроту) затухания с потенциально извлекаемыми запасами скважины.

Интегрируя от 0 до получаем выражение для накопленной добычи:

.

При накопленная добыча, если снять экономические ограничения, стремится к потенциально возможной , тогда находим:

и выражение можно записать в виде:

,

которую широко использовали В.Д. Лысенко и Э.Б.Мухарский для расчета дебита скважин при проектировании разработки месторождений. Она же вошла в методику Госплана СССР.

В 1945 году Дж. Арпс на основе статистической обработки материалов по большому числу скважин установил, что темп падения дебита нефти связан с его текущей величиной зависимостью типа:

,

где и - неотрицательные постоянные, а представляет собой дифференциальное уравнение. При уравнение Арпса описывает экспоненциальную функцию, поэтому выведенная им зависимость приводит к более общему закону.

Уравнение Арпса, применяется в международном аудите запасов для оценки коммерческой ценности нефтяных месторождений.

Теоретическое обоснование зависимости Дж.Арпса, было сделано Р.И.Медведским в 1987г. на основе трех предположений, а именно:

Функциональная связь между входным и выходным параметром некоторого процесса имеет физический смысл, если эти параметры объединены в безразмерные комплексы.

Функциональная связь не должна зависеть от произвола в выборе начала отсчета времени.

Вид функциональной зависимости остается неизменным при учете баланса массы вещества.

Для обоснования закона падения дебита скважины по нефти при обводнении допустим, что скважина эксплуатирует изолированную извне зону пласта, активные потенциально извлекаемые запасы, которой к началу эксплуатации равны . В ходе эксплуатации дебит скважины по нефти снижается от начального до текущего . Допуская зависимость одного безразмерного комплекса от другого в виде функции:

,

легко показать, что функция должна обладать следующими свойствами:

При переменном дебите по жидкости объем накопленной жидкости растет строго монотонно и поэтому его можно использовать в качестве аналога времени и можно получить общую зависимость:

.

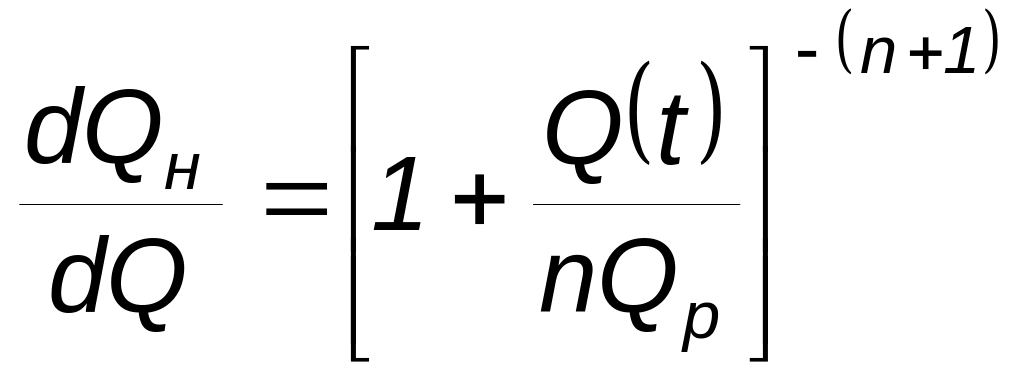Поскольку , то для дебита по нефти получаем формулу:

,

а для накопленной добычи

.

Данная зависимость получила название АЛГОМЕС-1 (Алгоритм Медведского Р.И.)

Так, Г.С. Камбаров и др. принимают , А.М. Пирвердян с соавторами полагает . Следует отметить, что каждый объект уникален и параметр характеризующий изменчивость коллекторских свойств необходимо определять по каждому объекту или группе объектов индивидуально.

Анализ основных объектов разработки, находящихся длительное время в эксплуатации, при использовании безразмерных параметров позволил установить характер выработки запасов по четырем группам пластов Сургутского свода: АС_8-9, АС_10-12, БС_1-4, БС_10-12. Ниже на рисунке представлены унифицированные кривые падения дебита нефти осредненной скважины по разным месторождениям от кратности промывки дренируемых запасов. Красным цветом показан прогноз на основании АЛГОМЕС-1 и указано значение параметра .

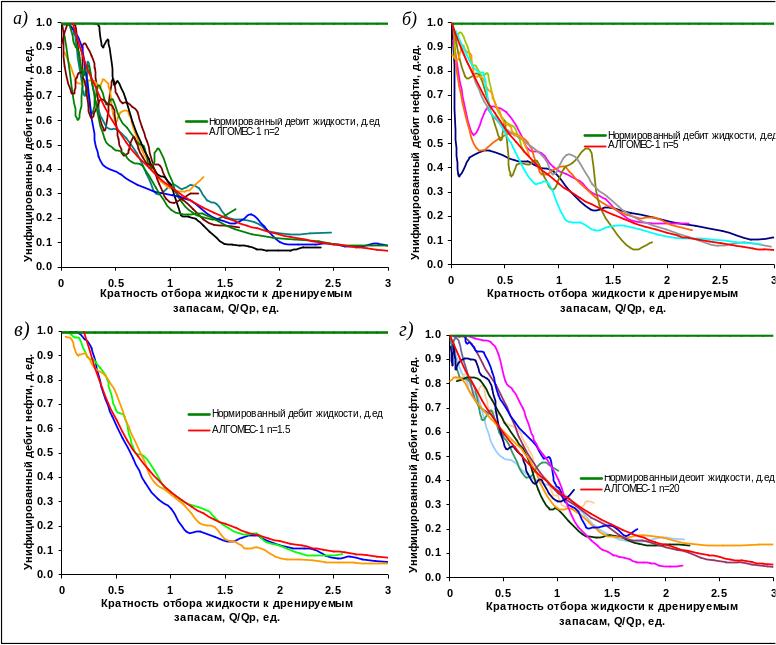
Рис. 5. Сопоставление характера выработки запасов по пластам

a) АС_8-9; б) АС_10-11; в) БС_1-2; г) БС_10-12

При анализе показателей разработки объекта и оценке эффектов от ГТМ эксперт сталкивается с проблемой «зашумления» кривой выработки запасов накладывающимися друг на друга эффектами от различного рода мероприятий. Основными из них являются: ввод и выбытие добывающих скважин, число которых ; мероприятия по интенсификации добычи нефти, оптимизации технологических режимов работы скважин и других ГТМ, влияющих на годовые отборы нефти и жидкости . Для проведения анализа выработки запасов предлагается воспользоваться динамикой показателей осредненной скважины, а именно, - использовать среднюю добычу нефти и жидкости на действующую скважину и тем самым снизить влияние динамики фонда на характер выработки запасов (рис.6 а, б).

С целью минимизации фактора наложения друг на друга эффектов от проводимых геолого-технических мероприятий по оптимизации режима работы скважины и интенсификации отборов предлагается преобразовать дебит жидкости в постоянную величину посредством введения приведенного времени , которое будет избирательно масштабировать шкалу времени. Приведенное время представляет собой отношение накопленной добычи жидкости к отбору жидкости в начальный момент времени . Так, при увеличении дебита жидкости относительно начального приведенное время будет больше реального и наоборот (рис.5в).

Таким образом, остается выразить дебит нефти относительно приведенного времени - . Полученные дебиты нефти и жидкости будут отражать эффективность ГТМ.

В дальнейшем индекс , поясняющий, что речь идет о показателях средней скважины, будем опускать.

Для сравнительного анализа выработки запасов нефти по пластам со схожими геолого-физическими свойствами предлагается унифицировать кривые падения дебита нефти представив их в безразмерном виде от кратности промывки дренируемых запасов (рис.6г). Очевидно, что кратность промывки запасов позволяет судить о степени вытеснения нефти из пласта.

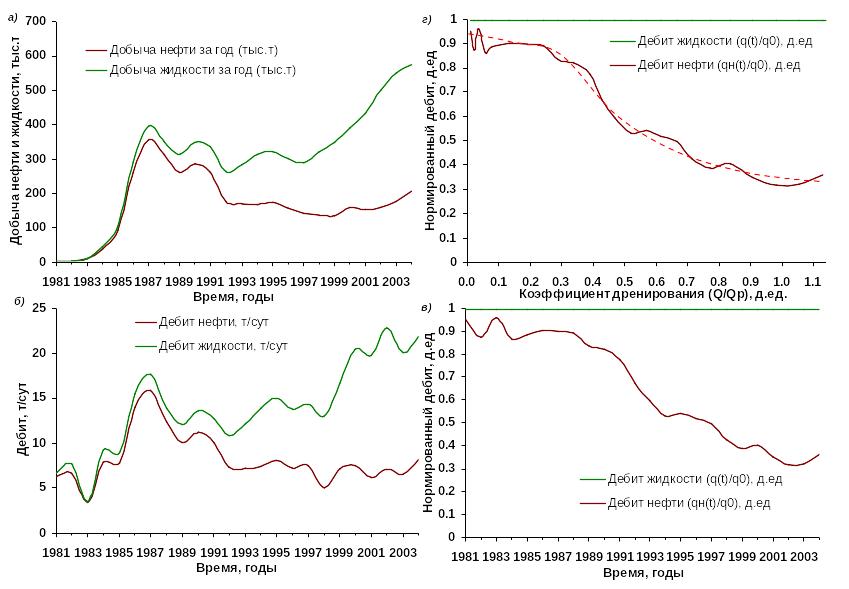
Рис. 6. Прием унификации кривой падения дебита нефти на примере объекта БС₁₀

На рис.6 приведен пример унификации кривой падения дебита нефти по пласту БС₁₀. Пунктирной линией обозначен общий характер поведения дебита осредненной скважины, первый прямолинейный участок соответствует безводному периоду эксплуатации, который сменяется падением. Участок монотонного убывания дебита нефти осложнен отдельными «всплесками», вызванными технологическими мероприятиями, которые свидетельствуют об их эффективности.

Задача 2: Используя результаты решения задачи №1 по определению входного дебита и оценке подвижных запасов рассчитать динамику добычи нефти по вариантам. Для прогноза использовать экспоненциальную зависимость падения дебита нефти.

По выбранному (варианту 400м) используя степенную зависимость произвести оценку чувствительности к возможным изменениям неоднородности пласта при .

Возможное представление результатов:

Таблица 3. Прогноз дебитов нефти по экспоненциальной зависимости

	, т		Период, годы / (сут=365*kисп(0,9)*kэкспл(0,95)
			1	2	3	4	5	6	7	8	9	10
			312	624	936	1248	1560	1872	2185	2497	2809	3121
100
150
….
600

Таблица 4. Прогноз дебитов нефти по зависимости АЛГОМЕС-1

	, т		Период, годы / (сут=365*kисп(0,9)*kэкспл(0,95)
			1	2	3	4	5	6	7	8	9	10
			312	624	936	1248	1560	1872	2185	2497	2809	3121
20
5
1,5
0,5