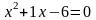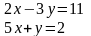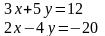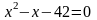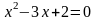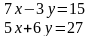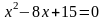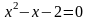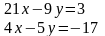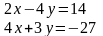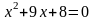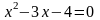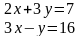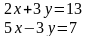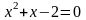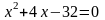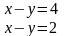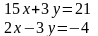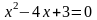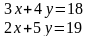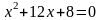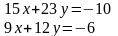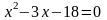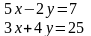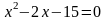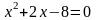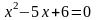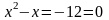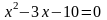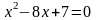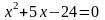Тема 2.3.1«Уравнения и неравенства»

ЗаданиеI. Перед выполнением внеаудиторной самостоятельной работы, прочитайте еще раз конспект, методические указания, литературу:

1.Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов. П.И. Самойленко,-3-е изд.,стереотип.-М.:Дрофа,2005.-395,(5)с.: ил.

2.Богомолов Н.В.Практические занятия по математике: Учеб. пособие для техникумов.-3-е изд., перераб. И доп.-М. : Высш.шк.,1990.-445 с.: ил.

3. Богомолов Н.В.Сборник задач по математике: : учеб. пособие для ссузов,-2-е изд.,испр.- М.:Дрофа,2005.-204.

Теоретические сведения по теме: «Уравнения и неравенства»».

Задание II.

Ответьте на контрольные вопросы (письменно):

1. Дайте определение уравнения с одной переменной.

2. Как записывается в общем виде линейное уравнение?

3. Какие уравнения называются равносильными?

4. Что называется корнем уравнения?

5. Сформулируйте теоремы, на основании которых решаются линейные уравнения.

6. Какой вид имеют линейные уравнения, имеющие одно решение, не имеющие решения и имеющие бесконечное множество решений?

7. Какие уравнения называются дробно-рациональными?

8. Дайте определение модуля действительного числа.

9. Перечислите основные свойства модуля действительного числа.

10. Что называется системой двух уравнений с одной переменной?

11. Что называется совокупностью двух уравнений с одной переменной?

12. Как выполняется решение линейных уравнений, содержащих переменную под знаком модуля?

13. Как выполняется решение линейных уравнений, содержащих переменную под знаком модуля?

14. 16.Что называется неравенством?

15. 17.Какие выражения называются алгебраическими, и какие числовыми неравенствами?

16. 18.Что называется решением неравенства?

17. Какие неравенства называются равносильными?

18. Перечислите основные свойства неравенств.

19. Какие неравенства называются линейными?

20. Какие неравенства не имеют решения?

21. Какому неравенству удовлетворяет любое число?

22. В каких случаях решение неравенства сводится к решению совокупности неравенства?

23. Какие уравнения с двумя переменными называются линейными?

24. Какие системы двух линейных уравнений с двумя переменными называются однородными и неоднородными?

25. Какие системы двух линейных уравнений с двумя переменными называются совместными и несовместными? Приведите примеры.

26. Как решаются в общем виде система двух линейных уравнений с двумя переменными?

27. Как составляется определитель второго порядка и каким знаком он обозначается?

28. Как составляют определения X и Y?

29. Как записываются формулы Крамера для решения системы двух линейных уравнений с помощью определителей?

30. При каком значении определителя система двух линейных уравнений с двумя переменными имеет одно решение?

31. Как записываются условия несовместности и неопределенности решения системы двух линейных уравнений с двумя переменными?

32. Как записываются формулы Крамера для решения системы трех линейных уравнений с тремя переменными?

33. При каком значении определителя система трех линейных уравнений с тремя переменными имеет бесконечное множество решений?

34. Как решается система трех линейных уравнений с тремя переменными методом Гаусса?

35. Какое уравнение называется квадратным уравнение общего вида и какое приведенным квадратным уравнением?

36. Выведите формулу корней квадратного уравнения общего вида.

37. Какое выражение называется дискриминантом квадратного уравнения общего вида?

38. Как по дискриминанту определяется характер уравнения?

39. Какие уравнения называются неполными квадратными?

40. Приведите примеры неполных квадратных уравнений и укажите способы их решения.

41. Докажите теорему Виета о свойстве корней квадратного уравнения.

42. Приведите примеры решения квадратного уравнения с использованием теоремы Виета.

43. Как составляются квадратные уравнения по его корням?

44. Как можно найти знаки корней квадратного уравнения, не решая уравнение?

45. Какое выражение называется квадратным трехчленом и как находится его корни?

46. По какой формуле квадратный трехчлен раскладывается на линейные множители?

47. Какое уравнение называется биквадратным, и как находятся его корни?

48. Какое уравнение называется двучленным, и как находятся его корни?

49. Приведите примеры частных случаев квадратной функции y=ax²+bx+c. Как называется график квадратной функции?

50. При каких значениях коэффициента a ветви графика функции y=ax²+bx+c направлены вверх (вниз)?

51. Как расположены ветви параболы по отношению к ее оси симметрии при различных значениях коэффициента a(a>1,0<a<1)?

52. Как найти абциссу вершины параболы, если она пересекается с осью Ox?

53. По каким формулам вычисляются координаты вершины любой параболы?

54. Какие неравенства называются квадратными неравенствами?

55. Перечислите возможные варианты решения квадратных неравенств графическим способом.

56. В каких случаях квадратное неравенство не имеет решения?

57. Какие неравенства можно решать методом промежутков?

58. Обьясните с помощью примеров применение метода промежутков при решении

59. Дайте определение с одной переменной.

60. Как записывается в общем виде линейное уравнение?

61. Какие уравнения называются равносильными?

62. Что называется корнем уравнения?

63. Сформулируйте теоремы, на основании которых решаются линейные уравнения.

64. Какой вид имеют линейные уравнения, имеющие одно решение, не имеющие решения и имеющие бесконечное множество решений?

65. Какие уравнения называются дробно-рациональными?

66. Дайте определение модуля действительного числа.

67. Перечислите основные свойства модуля действительного числа.

68. Что называется системой двух уравнений с одной переменной?

69. Что называется совокупностью двух уравнений с одной переменной?

70. Как выполняется решение линейных уравнений, содержащих переменную под знаком модуля?

71. Как выполняется решение линейных уравнений, содержащих переменную под знаком модуля?

72. Что называется неравенством?

73. Какие выражения называются алгебраическими и какие числовыми не равенствами?

74. Что называется решением неравенства?

75. Какие неравенства называются равносильными?

76. Перечислите основные свойства неравенств.

77. Какие неравенства называются линейными?

78. Какие неравенства не имеют решения?

79. Какому неравенству удовлетворяет любое число?

80. В каких случаях решение неравенства сводится к решению совокупности неравенства?

81. Какие уравнения с двумя переменными называются линейными?

82. Как решаются системы двух линейных уравнений с двумя переменными способами подстановки, алгебраического сложения ?

83. Какие системы двух линейных уравнений с двумя переменными называются однородными и неоднородными?

84. Какие системы двух линейных уравнений с двумя переменными называются совместными и несовместными? Приведите примеры.

85. Как решаются в общем виде система двух линейных уравнений с двумя переменными?

86. Как составляется определитель второго порядка и каким знаком он обозначается?

87. Как составляют определения X и Y?

88. Как записываются формулы Крамера для решения системы двух линейных уравнений с помощью определителей?

89. При каком значении определителя система двух линейных уравнений с двумя переменными имеет одно решение?

90. Как записываются условия несовместности и неопределенности решения системы двух линейных уравнений с двумя переменными?

91. Как записываются формулы Крамера для решения системы трух линейных уравнений с тремя переменными?

92. При каком значении определителя система трух линейных уравнений с тремя переменными имеет бесконечное множество решений?

93. Как решаются система трех линейных уравнений с тремя переменными методом Гаусса?

94. Какое уравнение называется квадратным уравнением общего вида и какое приведенным квадратным уравнением?

95. Выведите формулу корней квадратного уравнения общего вида.

96. Какое выражение называется дискриминантом квадратного уравнения общего вида?

97. Как по дискриминанту определяется характер уравнения?

98. Какие уравнения называются неполными квадратными?

99. Приведите примеры неполных квадратных уравнений и укажите способы их решения.

100. Докажите теорему Виета о свойстве корней квадратного уравнения.

101. Приведите Примеры решения квадратного уравнения с использованием теоремы Виета.

102. Как составляются квадратные уравнения по его корням?

103. Как можно найти знаки корней квадратного уравнения, не решая уравнение?

104. Какое выражение называется квадратным трехчленом и как находится его корни?

105. По какой формуле квадратный трехчлен раскладывается на линейные множители?

106. Какие уравнение называется биквадратным и как находятся его корни?

107. Какое уравнение называется двучленным и как находится его корни?

108. Приведите примеры частных случаев квадратной функции y=ax²+bx+c. Как называется график квадратной функции?

109. При каких значениях коэффициента a ветви графика функции y=ax²+bx+c направлены вверх (вниз)?

110. Как расположены ветви параболы по отношению к ее оси симметрии при различных значениях коэффициента a(a>1,0<a<1)?

111. Как найти абциссу вершины параболы, если она пересекается с осью Ox?

112. По каким формулам вычисляются координаты вершины любой параболы?

113. Какие точки графика функции y=ax²+bx+c называются характеристическими?

114. Приведите шесть вариантов построения графика функции y=ax²+bx+c.

115. Какие неравенства называются квадратными неравенствами?

116. Перечислите возможные варианты решения квадратных неравенств графическим способом.

117. При каком расположении графика квадратного трехчлена решением неравенства служит множество всех действительных чисел?

118. В каких случаях квадратное неравенство не имеет решения?

119. Какие неравенства можно решать методом промежутков?

120. Обьясните с помощью примеров применение метода промежутков при решении неравенств.

Задание III.

3.1 Решить квадратные уравнения двумя способами:

• По дискриминанту

• По теореме Виетта

3.2Решить систему линейных уравнений двумя способами:

• Способом алгебраического сложения

• Способом подстановки

Цель: Проверить уровень сформированности навыка решения квадратных уравнений и систем линейных уравнений.

Вариант 1

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

1. 

2. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

1. 

2. 

Вариант 2

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

1. 

2. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

1. 

2. 

Вариант 3

Задание3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

1. 

2. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

1. 

2. 

Вариант 4

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

2. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

1. 

2. 

3. Вариант 5

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

1. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

1. 

2. 

Вариант 6

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

1. 

2. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

1. 

2. 

Вариант 7

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

1. 

2. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

1. 

2. 

Вариант 8

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

Вариант 9

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

2. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

1. 

2. 

Вариант 10

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

1. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

2. 

Вариант 11

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

2. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

Вариант 12

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

1. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

3. Вариант 13

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

1. 

2. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

Вариант 14

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

2. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

Вариант 15

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

1. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

Вариант 16

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

1. 

2. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

2. 

Вариант 17

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

Вариант 18

Задание 3.1.

Решить квадратные уравнения двумя способами:

3. По дискриминанту

4. По теореме Виетта

4. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

3. Способом алгебраического сложения

4. Способом подстановки

Вариант 19

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

1. 

2. 

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

Вариант 20

Задание 3.1.

Решить квадратные уравнения двумя способами:

1. По дискриминанту

2. По теореме Виетта

Задание 3.2.

Решить систему линейных уравнений двумя способами:

1. Способом алгебраического сложения

2. Способом подстановки

Вариант 21

Задание 3.1.

Решить квадратные уравнения двумя способами:

3. По дискриминанту

4. По теореме Виетта

Задание 3.2.

Решить систему линейных уравнений двумя способами:

3. Способом алгебраического сложения

4. Способом подстановки

Вариант 22

Задание 3.1.

Решить квадратные уравнения двумя способами:

3. По дискриминанту

4. По теореме Виетта

Задание 3.2.

Решить систему линейных уравнений двумя способами:

3. Способом алгебраического сложения

4. Способом подстановки

Вариант 23

Задание 3.1.

Решить квадратные уравнения двумя способами:

3. По дискриминанту

4. По теореме Виетта

Задание 3.2.

Решить систему линейных уравнений двумя способами:

3. Способом алгебраического сложения

4. Способом подстановки

Вариант 24

Задание 3.1.

Решить квадратные уравнения двумя способами:

5. По дискриминанту

6. По теореме Виетта

Задание 3.2.

Решить систему линейных уравнений двумя способами:

5. Способом алгебраического сложения

6. Способом подстановки

Вариант 25

Задание 3.1.

Решить квадратные уравнения двумя способами:

3. По дискриминанту

4. По теореме Виетта

Задание 3.2.

Решить систему линейных уравнений двумя способами:

3. Способом алгебраического сложения

4. Способом подстановки

Вариант 26

Задание 3.1.

Решить квадратные уравнения двумя способами:

3. По дискриминанту

4. По теореме Виетта

Вариант 27

Задание 3.1.

Решить квадратные уравнения двумя способами:

3. По дискриминанту

4. По теореме Виетта

Задание 3.2.

Решить систему линейных уравнений двумя способами:

3. Способом алгебраического сложения

4. Способом подстановки

Вариант 28

Задание 3.1.

Решить квадратные уравнения двумя способами:

3. По дискриминанту

4. По теореме Виетта

Задание 3.2.

Решить систему линейных уравнений двумя способами:

3. Способом алгебраического сложения

4. Способом подстановки

Вариант 29

Задание 3.1.

Решить квадратные уравнения двумя способами:

7. По дискриминанту

8. По теореме Виетта

Задание 3.2.

Решить систему линейных уравнений двумя способами:

7. Способом алгебраического сложения

8. Способом подстановки

Вариант 30

Задание 3.1.

Решить квадратные уравнения двумя способами:

3. По дискриминанту

4. По теореме Виетта

Задание 3.2.

Решить систему линейных уравнений двумя способами:

3. Способом алгебраического сложения

4. Способом подстановки

3.3: Решите систему способами алгебраического сложения,подстановки и графическим:( Богомолов Н.В.Сборник задач по математике: : учеб. пособие для ссузов,- 2-е изд.,испр.- М.:Дрофа,2005 (стр11)

Вариант 1-№45.1; Вариант 2-№45.2; Вариант 3-№45.3; Вариант 4-№45.4

3.4 Решите систему по формулам Крамера (стр11-12):

Вариант 1-№51.1; Вариант 2-№51.2; Вариант 3-№51.3; Вариант 4-№51.4

Вариант 1-№52.1; Вариант 2-№52.2; Вариант 3-№52.3; Вариант 4-№52.4

3.5 Решите систему с применением метода Гаусса:

Вариант 1-№53.1; Вариант 2-№53.2; Вариант 3-№53.3; Вариант 4-№53.4

3.6 Составьте квадратное уравнение по его корням:( Богомолов Н.В.Сборник задач по математике: : учеб. пособие для ссузов,- 2-е изд.,испр.- М.:Дрофа,2005 (стр13)

Вариант 1-№58.1; Вариант 2-№58.2; Вариант 3-№58.3; Вариант 4-№58.4

3.7Решите биквадратное уравнение :( Богомолов Н.В.Сборник задач по математике: : учеб. пособие для ссузов,- 2-е изд.,испр.- М.:Дрофа,2005 (стр13)

Вариант 1-№62.1; Вариант 2-№62.2; Вариант 3-№62.3; Вариант 4-№62.4

3.8 Решите неравенства:( Богомолов Н.В.Сборник задач по математике: : учеб. пособие для ссузов,- 2-е изд.,испр.- М.:Дрофа,2005 (стр15)

Вариант 1-№66.1; Вариант 2-№66.2; Вариант 3-№66.3; Вариант 4-№66.4

Вариант 1-№67.1; Вариант 2-№67.2; Вариант 3-№67.3; Вариант 4-№67.4

Вариант 1-№69.1; Вариант 2-№69.2; Вариант 3-№69.3; Вариант 4-№69.1

3.9Решите иррациональные уравнения:( Богомолов Н.В.Сборник задач по математике: : учеб. пособие для ссузов,- 2-е изд.,испр.- М.:Дрофа,2005 (стр16)

Вариант 1-№70.1; Вариант 2-№70.2; Вариант 3-№70.3; Вариант 4-№70.4

Вариант 1-№71.1; Вариант 2-№71.2; Вариант 3-№71.3; Вариант 4-№71.4

Вариант 1-№72.1; Вариант 2-№72.2; Вариант 3-№72.3; Вариант 4-№72.4

3.10 Решите иррациональные неравенства:( Богомолов Н.В.Сборник задач по математике: : учеб. пособие для ссузов,- 2-е изд.,испр.- М.:Дрофа,2005 (стр17)

Вариант 1-№74.1; Вариант 2-№74.2; Вариант 3-№74.3; Вариант 4-№74.4

Вариант 1-№75.1; Вариант 2-№75.2; Вариант 3-№75.3; Вариант 4-№75.4

Вариант 1-№76.1; Вариант 2-№76.2; Вариант 3-№76.3; Вариант 4-№76.4

ЗаданиеIV.

Проведите анализ выполненной работы.