Государственное бюджетное образовательное учреждение

среднего профессионального образования Свердловской области «Талицкий лесотехнический техникум имени Н.И.Кузнецова»

Задания для выполнения внеаудиторной самостоятельной работы по дисциплине «Математика»

Разработала: Зыкова Любовь Васильевна

Преподаватель ТЛТ

Талица 2013

Содержание

Введение…………………………………………………………………………..3

I.Основная часть……………………………………………………………….....4

Тема 1.1 Развитие понятия о числе……………………………………………...4

Тема 1.2Корни степени и логарифмы……………………………………….…

Тема 1.3 Основы тригонометрии…………………………………………………

Тема 1.4 Функции, их свойства и графики……………………………………….

Тема 1.5 Степенные, показательные, логарифмические и тригонометрические функции…………………………………………………………………………….

Тема 2.1 Последовательности…………………………………………………….

Тема 2.2 Производная………………………………………………………….

Тема2.3 Уравнения и неравенства………………………………………………

Тема 3.1Элементы комбинаторики………………………………………….

Тема3.2 Элементы теории вероятностей…………………………………

Тема3.3 Элементы математической статистики……………………………..

Тема 4.1 Прямые и плоскости в пространстве…………………………….

Тема 4.2 Многогранники………………………………………………………..

Тема 4.3 Тела и поверхности вращений…………………………………….

Тема 4.4 Измерения в геометрии…………………………………………..

Тема 4.5 Координаты и векторы……………………………………………….

Список литературы…………………………………………………………

Введение

Переход на новые образовательные стандарты сопровождался определением задач, места, количества часов, содержания, форм работы в учебной плане самостоятельной внеаудиторной работы студентов. Одной из составляющих ФГОС является увеличение числа часов, отводимых на внеаудиторную самостоятельную работу студентов. Считается, что специалист со средним специальным образованием должен постоянно самостоятельно совершенствовать свои знания. А для этого необходимо уметь самостоятельно приобретать знания.

В нормативных документах определены цели самостоятельной внеаудиторной работы студентов:

- закрепление, углубление, расширение и систематизация знаний, полученных во время аудиторных занятий, самостоятельное овладение новым учебным материалом;

- формирование общетрудовых и общепрофессиональных умений;

- формирование умений и навыков самостоятельного умственного труда;

- развитие самостоятельности мышления;

- формирование убежденности, волевых черт характера, способности к самоорганизации.

Самостоятельные работы студентов прослушиваются на занятиях, анализируются преподавателем, оцениваются по 5-ти балльной системе с выставлением оценки в журнал.

Воспитание морально-волевых качеств студентов – важнейшая функция внеаудиторной самостоятельной работы. Нельзя забывать, что требованием времени является воспитание инициативы, активности – качеств, без которых невозможен творческий труд, который и лежит в основе самостоятельной работы студентов.

3.

Тема 1.1 Развитие понятия о числе.

4.

ЗаданиеI. Перед выполнением внеаудиторной самостоятельной работы, прочитайте еще раз конспект, методические указания, литературу:

1.Богомолов Н.В. Математика: учеб. для ссузов / Н.В. Богомолов. П.И. Самойленко,-3-е изд.,стереотип.-М.:Дрофа,2005.-395,(5)с.: ил.

2.Богомолов Н.В.Практические занятия по математике: Учеб. пособие для техникумов.-3-е изд., перераб. И доп.-М. : Высш.шк.,1990.-445 с.: ил.

3. Богомолов Н.В.Сборник задач по математике: : учеб. пособие для ссузов,-2-е изд.,испр.- М.:Дрофа,2005.-204.

Теоретические сведения по теме: «Развитие понятия о числе».

Числа, полученные в результате счета, называются натуральными. Множество натуральных чисел обозначаются

Целые числа – бывают положительными и отрицательными. Совокупность целых чисел образует множество целых чисел. Число видов, 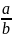где а и b целые числа, причём 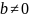называется рациональным числом. Множество, состоящее из положительных и отрицательных дробных чисел, называется множеством рациональных чисел.

Действие с положительными и отрицательными числами.

1. 18-20=-2

2. -3+7=4

3. -11+18=7

4. -12+19=-7

5. 17-30=-13

6. 12-(-6)=18

7. -11+(-7)=-18

8. 12/(-3)=-4

Признаки делимости чисел.

На 2 все чётные;

На 3 сумма чисел должна делиться на 3;

На 4 если 2 крайние цифры делятся на 4;

На 5 все числа, которые оканчиваются на 5 и на 0

На 6 числа, которые делятся на 3 и на 2

На 10 все числа, у которых на конце 0

5.

Периодические дроби.

1. Определение: Периодические дроби бывают чистыми и смешанными.

Чистой периодической дробью называется дробь, у которой период

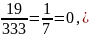142857 .

Смешанной называется дробь, у которой между запятой и первым периодом есть одна или несколько повторяющихся цифр:

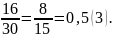
Чтобы обратить чистую периодическую дробь в обыкновенную нужно ее период сделать числителем, а в знаменателе столько раз надо написать «9» сколько в периоде чисел.

Обращение смешанной периодической дроби в обыкновенную:

Чтобы обратить смешанную периодическую дробь достаточно из числа до второго периода вычесть число стоящее до первого периода, и полученную разность взять числителем , а знаменателем написать цифру в периоде столькими нулями сколько цифр между запятой и периодом:

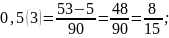
0,0(142857)=

Действительные числа.

Бесконечная непериодическая дробь называется рациональным числом:

=1,4142135…

=3,14

Иррациональные вместе с рациональными числами образуют область действительных чисел.

Действительным числом называется конечная или бесконечная периодическая дробь.

Q-это множество всех рациональных чисел.

Y- множество всех иррациональных чисел..

R- множество действительных чисел.

Комплексные числа.

Термин «комплексные числа» ввел немецкий математик Карл Гаус.

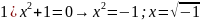
Введём новое понятие: j- мнимая единица :

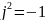
x=±

1. комплексными числами - называется числа вида Z= a+b j где a и d действительные числа, а число мнимая единица.

2. Комплексные числа называются взаимно сопряженными, если их действительные части равны, а мнимые отличаются знаками

Например число:

Z=-3+5j

Z=-3-5(-j)

Z=-3+5j

Z=5-7j

Z=5=7j

Множество комплексных чисел обозначается буквой С

Комплексное число сложно изобразить тоской или соответствующим вектором на комплексном

Модулем Z=a+bj называется действительным числом Ч= Модуль действительного числа, называется также абсолютной величиной этого числа.

Сложение комплексных чисел.

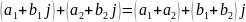
Деление комплексных чисел.

=

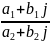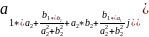
Задание II.

Ответьте на контрольные вопросы (письменно):

1.Какие числа называются натуральными? Какое значение введено для множества натуральных чисел?

2.Какое множество называется множеством рациональных чисел и как это

множество обозначается?

3.Какие обыкновенные дроби обращаются в конечные десятичные?

4. Какие числа входят в множество целых чисел? Какое обозначение принято для этого множества?

5. Перечислите основные законы действий над рациональными числами.

6. Какие обыкновенные дроби выражаются только приближенными десятичными?

7. Какие десятичные дроби называются бесконечными периодическими?

8 . Что называется периодом бесконечной периодической десятичной дроби?

9. Какие периодические дроби называются чистыми и смешанными и как сокращенно они записываются?

10. Как записываются целые числа и конечные десятичные дроби в виде бесконечных периодических дробей?

11.Любая ли бесконечная периодическая десятичная дробь является рациональным числом?

12. Как обратить чистую периодическую десятичную дробь в обыкновенную?

13.Как обратить смешанную периодическую десятичную дробь в обыкновенную?

14. Какое исключение представляет собой бесконечная периодическая десятичная дробь с периодом 9?

15. Какие числа называются действительными иррациональными и как обозначается множество иррациональных чисел?

16.Докажите, что не существует числа, квадрат которого равен 2.

17. Какие числа называются действительными и какое для них введено обозначение?

18.Какими свойствами обладает множество действительных чисел?

19. Что называется числовой прямой?

20 .Что называется числовым отрезком?

21. Что называется числовым интервалом?

22.Какие промежутки называются полуоткрытыми?

23 .Какие промежутки называются бесконечными?

24 .Что понимается под абсолютной величиной действительного числа?

25. Почему нельзя делить на нуль?

26. Какие числа называются комплексными и мнимыми?

27. Как геометрически представляется комплексное число?

28. Что называется модулем комплексного числа?

29. Как выполняется сложение и вычитание комплексных чисел?

30. Как геометрически представляется сумма двух комплексных чисел?

31. Как выполняется умножение комплексных чисел?

32. Как выполняется деление комплексных чисел?

33. Как выполняется возведение в степень мнимых и комплексных чисел?

Задание III.

3.1 Выполнить действия согласно своего варианта,

30 вариантов по 1 заданию.

Цель: Закрепить навык на все действия с дробями

Вариант 1

Выполнить действия:

Вариант 2

Вычислить:

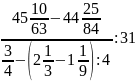
Вариант 3

Вычислить:

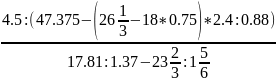
Вариант 4

Вычислить:

(

Вариант 5

Найти число, если 3.6% его составляют

Вариант 6

Найти x из пропорции:

+1

Вариант 7

Найти x, если:

Вариант 8

Вычислить:

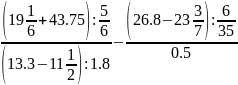
Вариант 9

Вычислить:

1.32:(1.17:1.3+8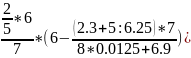

Вариант 10

Найти 72% от числа:

Вариант 11

Найти число, если 26% его составляют:

Вариант 12

Вычислить:

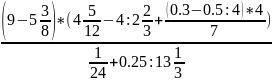
Вариант 13

Вычислить:

3.25-(

Вариант 14

Найти x из пропорций:

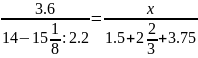
Вариант 15

Найти x, если:

Вариант 16

Вычислить:

Вариант 17

Вычислить:

Вариант 18

Вычислить:

(

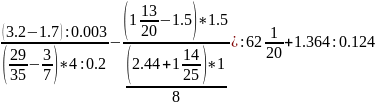
Вариант 19

Найти число, 3.6% которого составляют:

Вариант 20

Найти x из пропорции:

=

Вариант 21

Найти x, если:

Вариант 22

Вычислить:

Вариант 23

Вычислить:

1.32:(1.17:1.3+8

Вариант 24

Найти 72% от числа: 1314-2527-1056*230.04+46.750.01

Найти число, если 26% его составляют:

Вариант 26

Вычислить:

Вариант 27

Вычислить:

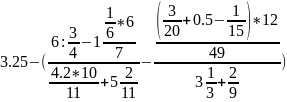*2

Вариант 28

Найти x из пропорции:

Вариант 29

Найти x, если:

Вариант 30

Вычислить:

3.2Решить задачи:.( Богомолов Н.В.Сборник задач по математике: : учеб. пособие для ссузов,- 2-е изд.,испр.- М.:Дрофа,2005 (стр4-5)

Обратите обыкновенные дроби в десятичные периодические:

Вариант 1-№1.1; Вариант 2-№1.2; Вариант 3-№1.3; Вариант 4-№1.4

Обратите чистые периодические десятичные дроби в обыкновенные:

Вариант 1-№2.1; Вариант 2-№2.2; Вариант 3-№2.3; Вариант 4-№2.4

Обратите смешанные периодические десятичные дроби в обыкновенные:

Вариант 1-№3.1; Вариант 2-№3.2; Вариант 3-№3.3; Вариант 4-№3.4

3.3Выполнить действия: ( Богомолов Н.В.Сборник задач по математике: : учеб. пособие для ссузов,- 2-е изд.,испр.- М.:Дрофа,2005 (стр4-5)

Сложение комплексных чисел:

Вариант 1-№4.1; Вариант 2-№4.2; Вариант 3-№4.3; Вариант 4-№4.4

Разность комплексных чисел:

Вариант 1-№6.1; Вариант 2-№6.2; Вариант 3-№6.3; Вариант 4-№6.4

Произведение комплексных чисел:

Вариант 1-№7.1; Вариант 2-№7.2; Вариант 3-№7.3; Вариант 4-№7.4

3.4 Вычислить:

Вариант 1-№8.1; Вариант 2-№8.2; Вариант 3-№8.3; Вариант 4-№8.4

Вариант 1-№9.1; Вариант 2-№9.2; Вариант 3-№9.3; Вариант 4-№9.4

Вариант 1-№10.1; Вариант 2-№10.2; Вариант 3-№10.3; Вариант 4-№10.4

ЗаданиеIV.

Проведите анализ выполненной работы.