Особенности распределений температуры в плоских проводниках различной конфигурации

Герасименко Т. Н., Поляков П. А.

МГУ имени М. В. Ломоносова, Физический факультет

Исследованы стационарные распределения температур в плоских проводниках различной конфигурации при протекании по ним постоянного электрического тока. Было обнаружено, что распределения температуры определяются не только свойствами материала, но и характерными размерами проводника и могут не коррелировать с распределениями тока. Установлены критерии подобия распределений температуры в геометрически подобных плоских проводниках.

Введение

В работах [1,2] нами исследовались распределения плотности постоянного тока в плоских проводниках различной конфигурации. Под плоскими понимались проводники, толщина τ которых много меньше их линейных размеров. Во всех полученных результатах имеется одна общая черта — в каждом из проводников есть одна или несколько областей, плотность тока в которых стремится к бесконечности или (при скруглении близлежащего угла) существенно превышает плотность тока во всех остальных частях проводника (Рис. 1).

Естественно, что именно в этих областях в силу закона Джоуля–Ленца будет выделяться максимальное количество теплоты и, казалось бы, естественно предполагать, что именно там проводник будет сильнее всего нагреваться. В работе [3] нами был аналитически исследован случай сингулярности в распределении тока в задаче с цилиндрической симметрией и было изучено влияние соотношения коэффициента теплопроводности и коэффициента теплоотдачи с поверхности проводника на распределение температуры. Было обнаружено, что наличие объемной теплопроводности существенно сглаживает неоднородность в выделении тепла и тем самым делает распределение температуры существенно отличным от распределения выделяемой тепловой мощности, однако максимум температуры совпадал с максимумом плотности тока.

Очевидно, сходная ситуация имеет место и для проводников, рассмотренных в работах [1,2], в силу наличия в них областей с резко возрастающей плотностью тока, однако, в силу их сложной формы аналитическое решение уравнения теплопроводности уже невозможно, что приводит к необходимости использования численных методов.

Уравнение теплопроводности в безразмерных переменных

Подобно тому, как это сделано в [3], учитывалось, что на распределение тепла влияет объемная теплопроводность и теплоотдача с поверхности проводника. Для описания теплоотдачи с поверхности использовался закон Ньютона–Рихмана с эффективным коэффициентом теплоотдачи [4-7], который предполагался постоянным.

Учитывалось, что для большинства металлов зависимость удельного сопротивления от температуры описывается линейной функцией в большом диапазоне температур [8,9]:

,

где α — температурный коэффициент сопротивления, θ — температура окружающей среды, которая предполагалась постоянной, ρ_θ — удельное сопротивление материала проводника при этой температуре, T — искомая температура проводника.

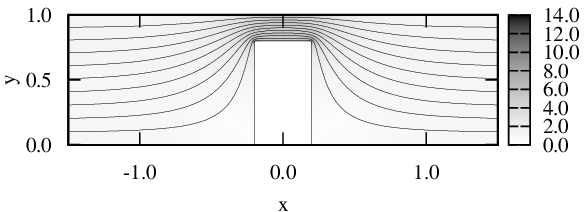
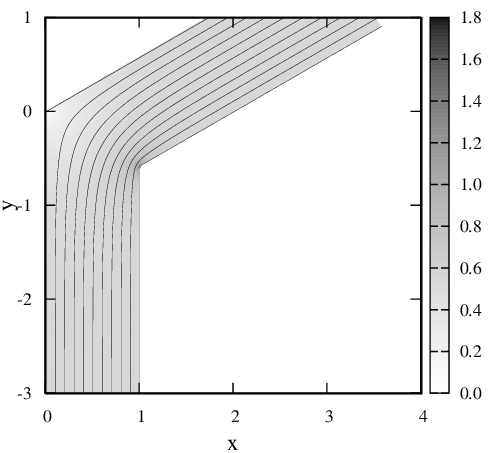
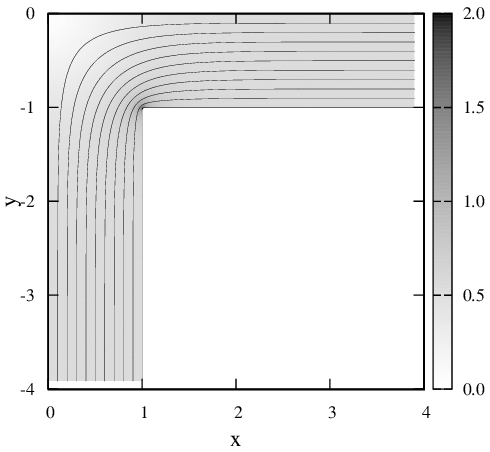
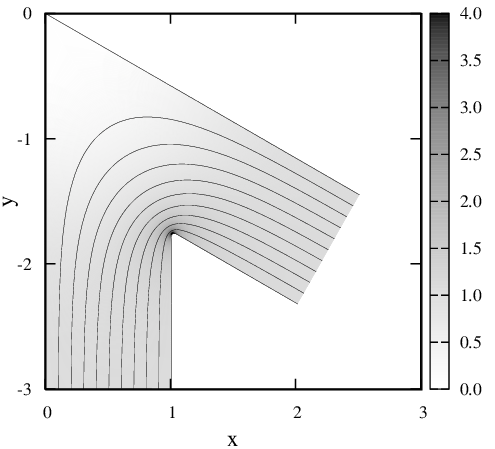
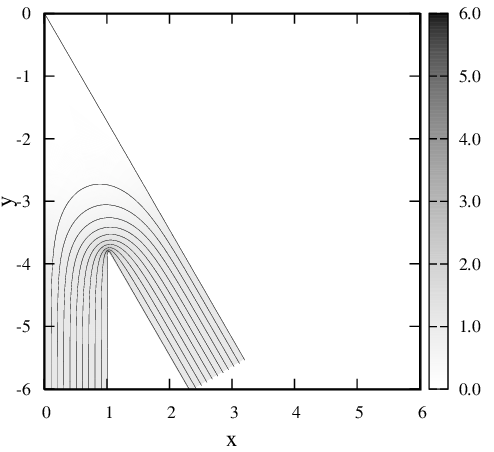
Рис. 1 Нормированные распределения плотности тока j(x,y)/j_∞ и линии тока, полученные в работах [1,2], j_∞ — плотность тока на бесконечном удалении от неоднородности.

Как и в работе [3], уравнение теплопроводности было записано в виде:

,

здесь , β — коэффициент теплопроводности, h_T — эффективный коэффициент теплоотдачи, τ — толщина проводника.

Поскольку распределения токов в геометрически подобных проводниках также подобны, то в тех случаях, когда у рассматриваемых проводников совпадают плотности тока, подобными будут являться и распределения выделяемой тепловой энергии. Однако, за перераспределение этой энергии по проводнику отвечает объемная теплопроводность, которая описывается законом Фурье, то есть зависит от градиента температур, а стало быть и от характерных размеров проводника.

Для того, чтобы исследовать вопрос о подобии распределений температуры, уравнение было записано в безразмерных переменных, число которых, согласно Π-теореме Бакингема [10], может быть сведено к 3-м:

,

где

,

L, T — характерные величины длины и температуры соответственно, Δ_Π — оператор Лапласа в безразмерных координатах, , и .

Из выражений следует, что на вид распределений температуры, как и предполагалось, оказывают влияние характерные размеры проводников. Как видно, параметр П₁ пропорционален квадрату характерного размера проводника, но не зависит от тока, протекающего через этот проводник. Это говорит о том, что при изменении характерных размеров проводника изменяется вид уравнения , а, следовательно, и его решение.

При решении этого уравнения предполагалось, что проводник с боков окружен полностью теплоизолирующим материалом, и отток тепла через боковые границы отсутствует. Для численного решения, необходимо было выделить какую-то конечную область проводника. Согласно работам [1,2], во всех рассматриваемых проводниках распределение тока становится равномерным на некотором удалении от неоднородности. На этом расстоянии, перпендикулярно границам проводника и выбирались границы области. Это предположение позволило считать, что в силу равномерности распределения тока, а, следовательно, и источников тепла, градиент температуры можно считать пренебрежимо малым. Т.е. считать, что на всей границе рассматриваемой области проводника заданы условия Неймана.

здесь Ω — рассматриваемый участок проводника в безразмерных координатах. Эта задача, согласно [11], эквивалентна задаче о минимизации функционала

что позволило применить для её решения метод конечных элементов. Полученная при использовании треугольных элементов система линейных уравнений имеет вид:

,

где G — число узлов в триангуляции,

.

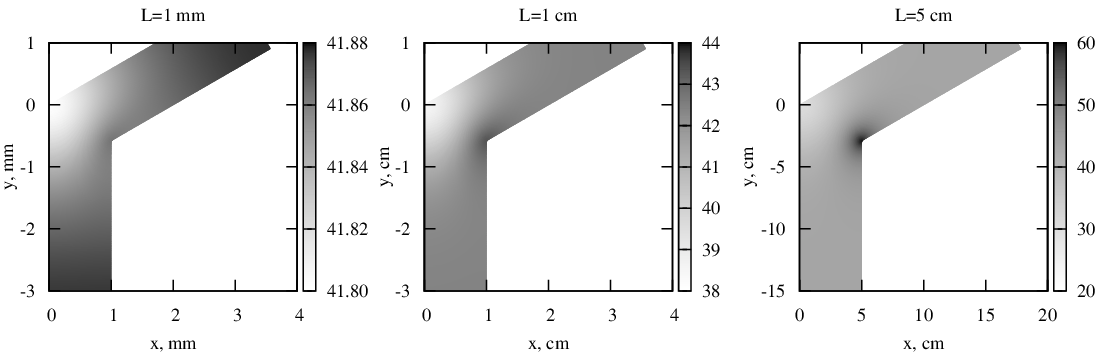
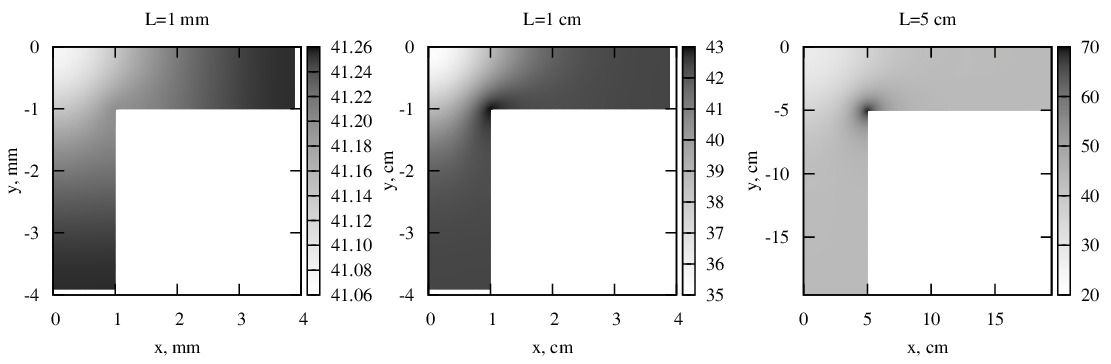
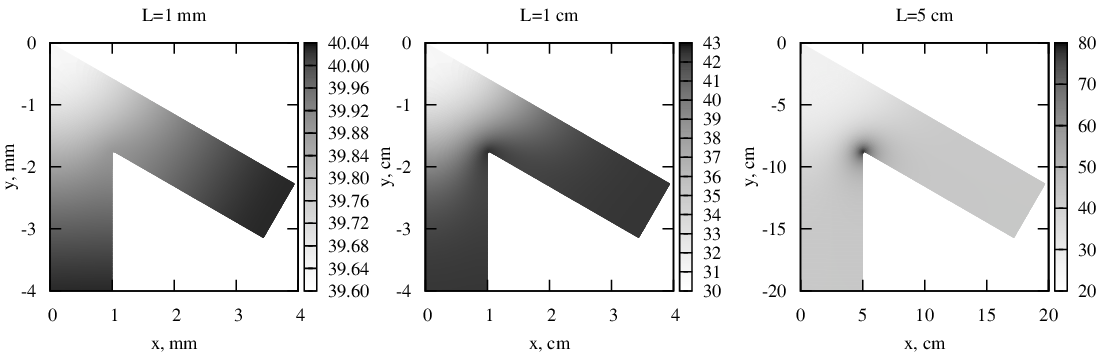
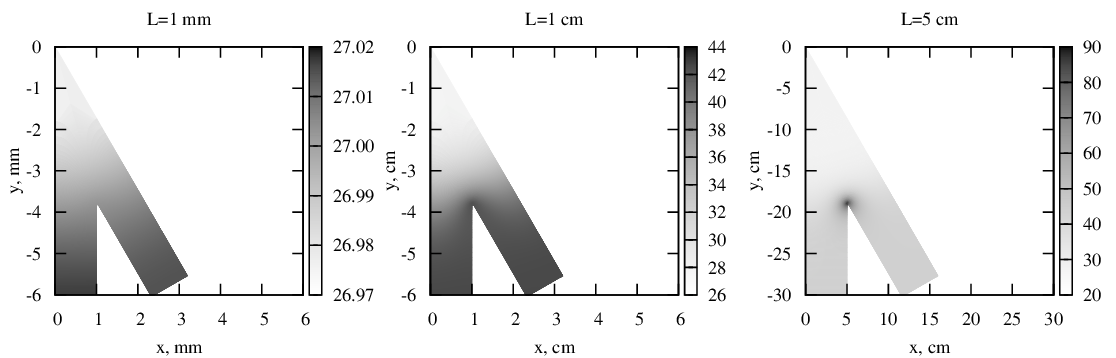
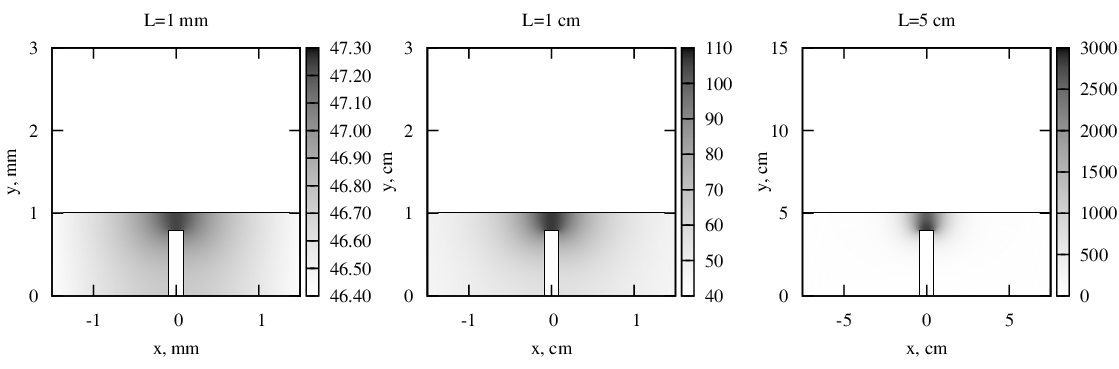
Рис. 2 Распределения температуры в геометрически подобных проводниках различной формы.

Индексы i, j, k пробегают значения от 1 до 3; величины A, b и c различны для каждого элемента:

.

Здесь (X_j,Y_j) — координаты j-й вершины элемента. i, j, k получаются друг из друга циклическими перестановками; A — площадь элемента.

При технической реализации этого метода нами использовался тот факт, что все рассматриваемые в работах [1,2] области были получены из верхней комплексной полуплоскости с помощью конформных отображений. Это позволило выбирать точки для триангуляции не в самой области Ω, а в соответствующем ей полукольце верхней комплексной полуплоскости, что, в свою очередь, позволило избежать трудностей с выбором точек на границе и использовать один и тот же алгоритм для всех рассматриваемых областей.

Для построения триангуляции Делоне была использована программа «Triangle» [12], для решения системы уравнений — библиотека UMFPACK [13].

Результаты решения для алюминиевых проводников толщиной τ = 10 мкм, по которым течет ток плотностью j_∞ = 50 А/мм² приведены на рисунке 2. Температура окружающей среды θ = 26,6 ^оC, параметры материала: ρ = 0,0292 Ом мм²/м, β = 226 Вт/(K м), h_T = 49,6 Вт/(K м²), α = 0,0042 1/К. Видно, что при изменении характерных размеров L распределения температуры весьма существенно изменяются и температура в точке с максимальной плотностью тока может быть не только больше, но и меньше температуры удаленных от неоднородности частей проводника. Кроме того, в проводниках с меньшими характерными размерами разброс температур оказывается намного меньше, чем в проводниках с большими размерами, поэтому при недостаточной точности измерительных приборов они могут выглядеть равномерно нагретыми.