Порядок выполнения работы.

1. Определить, сколько двоичных разрядов требуется для представления входных и выходных функций.

2. Построить таблицу истинности выходных функций, соответствующую заданной таблице преобразования.

3. Представить выходные функции в виде СДНФ или СКНФ, если нулевых значений функции значительно меньше, чем единичных.

4. Минимизировать выходные функции методом карт Карно, получив МДНФ.

5. Выполнить моделирование преобразователя в Excel.

6. Исправить ошибки.

7. Применить закон де Моргана, и представить выходные логические функции в базисе И – НЕ.

8. Построить структурные схемы преобразователя в двух базисах И – ИЛИ –НЕ, и И – НЕ.

9. Представить и защитить отчет.

Примеры результатов выполнения некоторых пунктов работы.

Приведенные примеры соответствуют заданию табл.1.

Табл.2. Таблица истинности функций преобразователя.

К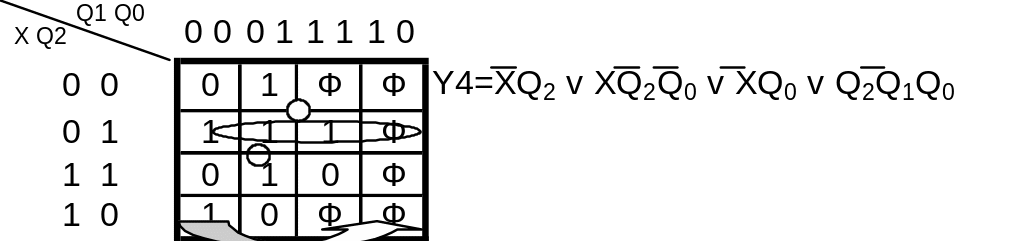 арта Карно для функции Y₄ и МДНФ

На карте показаны группы склеенных клеток. Соседние клетки, содержащие значения 1 и Ф склеиваются. Можно склеивать число клеток кратное степени двух – 2, 4, 8, 16. Каждой группе клеток соответствует импликанта их покрывающая. Импликанты в формуле соединяются знаком дизъюнкции. Добавление в группу двух клеток уменьшает количество переменных в импликанте на 1. В импликанту входят переменные значения которых одинаково в наборах всех клеток. Если значение переменной в наборах равно единице, то переменная входит в импликанту в прямом виде, если нулю, то – в инверсном. Если единица расположена на карте изолированно, то ей соответствует конституента 1, содержащая все переменные в соответствии с набором, на котором она получена. При разбиении клеток на группы следует придерживаться таких положений: Каждую единицу нужно включить в как можно крупную группу; количество групп должно быть как можно меньше, то есть не следует объединять единицы в группу, если все они уже объединены в других группах. Далее на рис.1 приведена модель преобразователя в Excel, формула вычисления Y₄, отображается в строке формул.

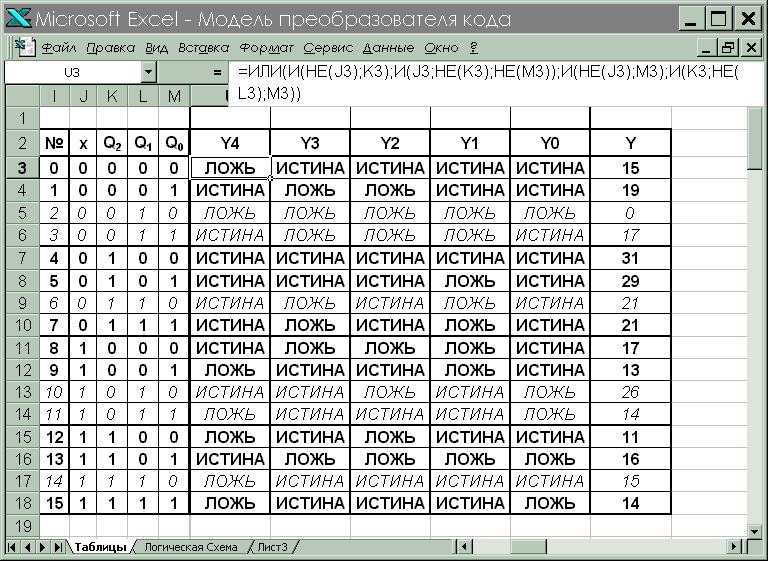
Рис.2. Модель преобразователя в Excel.

Содержание отчета.

В отчете должны быть пункты, соответствующие всем пунктам раздела «Порядок работы». Отчет начинается разделом «Введение», в котором формулируется задание и планработы, и заканчивается разделом «Заключение», в котором должны быть сделаны выводы о проделанной работе.

Контрольные вопросы.

1. Какая задача поставлена в работе?

2. Пояснить таблицу соответствия кодов (табл.1).

3. Что означает буква Ф в таблице истинности?

4. Метод минимизации по картам Карно.

5. По структурной схеме и заданным значениям x и Q определить значение Y в десятичной системе счисления.

6. На каком пункте проектирования ,буква Ф таблице истинности получает конкретное значение?

Дополнительные сведения. Законы алгебры логики.

Свойства логического сложения, умножения и инверсии

0  0 = 0; 0 * 0 = 0; 0 = 1;

0 0*0; 1 = 0;

1 x = x.

1 … 

x  1 = 1; x * 1 = x;

x  x = x; x * x = x;

x  x  …  x = x; x * x * … *x = x;

x  0 = x; x * 0 = 0;

x  x = 1; x * x = 0;

Основные законы и правила булевой алгебры соответственно для логического сложения и умножения.

Переместительный (коммутативный) закон:

x  y = y  x; x*y = y*x;

Сочетательный ( ассоциативный) закон:

(x  y)*z = x*(y  z); (x*y)*z = x*(y*z);

Распределительный (дистрибутивный) закон:

z*(x  y) = xz  yz; (z  x)(z  y) = z  xy;

Правило поглощения:

x  xy = x; x*(x  y) = x.

Правило склеивания:

xy  x*y = x; (x  y)(x  y) = x.

Закон двойственности или правило де Моргана:

(x  y) = x * y;

(x*y) = x  y.